摘 要: 培养学生的数学核心素养, 是小学数学教学的重要目标。如何理解其本质特征?如何在具体的教学过程中真正地将这种核心素养的培育落到实处?作为教师, 要有效地利用课本知识与相关例题, 由浅入深, 由表及里, 不断追问, 启发思考, 帮助学生逐渐学习分析比较, 感悟数学思想, 建构认知系统, 进一步促进学生数学核心素养的提升。
关键词: 小学数学; 折线统计图; 核心素养;

Abstract: Fostering students' core attainments is the important goal of primary school mathematics education. How should teachers understand its essence? And how can they truly realize the goal of fostering such core attainments in the process of teaching? To solve the above problems, teachers need to make eff ective use of textbook knowledge and related examples by employing such methods as from the shallower to the deeper, from the outside to the inside, and by keeping probing, to enlighten students' thinking and help them gradually learn to analyze and compare so that they can gain insights into mathematics thoughts and construct their cognitive systems, further promoting their mathematical core attainments.
Keyword: primary school mathematics; broken-line cartogram; core attainment;
2014年, 教育部发布了《关于全面深化课程改革, 落实立德树人根本任务的意见》, 提出了“核心素养”这一重要概念, 并要求将此作为深化课程改革的关键环节, 培养学生的核心素养便成为教育界十分关注的热点。那么, 在小学数学教学中, 我们该如何解读并着力培养学生的核心素养呢?
根据2011版的新课程标准的要求, 义务教育阶段小学数学教学的总目标是:通过数学教学, 使学生获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验;体会数学知识之间、数学与其他学科之间、数学与生活之间的联系, 运用数学的思维方式进行思考, 增强发现和提出问题的能力、分析和解决问题的能力。首都师范大学的王尚志教授在《数学核心素养与小学数学教学》的报告中指出:数学学科的核心素养可以确定为“数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析”等六个方面。
数学核心素养是学生在数学学习过程中形成的, 在各种社会生活中积极运用数学知识和数学思维分析、解决各种问题, 发挥数学应用价值, 实现自身与社会持续发展的最基本、最具有生长性的相关的数学素养, 是学生适应个人终身发展和社会发展需要的必备品格和关键能力。而数学是研究数量关系和空间形式的科学, 数学的学习离不开思维, 思维是数学的本质特征。数学抽象、逻辑推理、认知系统、数学思想、数据分析等都是数学思维的具体体现, 因此, 数学教学中, 我们可以从数学的本质出发, 引导学生进行有效的探究, 从而把培养学生的数学核心素养落到实处。笔者以苏教版教材小学数学五年级下册《折线统计图》一课的教学为例, 谈谈自己有关的一些教学实践与思考。
一、在激发内需中培养数学思维
美国着名的心理学家布鲁纳认为:最好的学习动机是学生对所学知识本身的内在兴趣。兴趣是学生学习的内驱力, 学生学习的效果最终取决于他们在学习活动中智力因素和非智力因素的投入程度。因此, 激发学生的学习需求, 引导他们积极主动地开展探究活动, 是提升学生数学核心素养的重要前提。
五年级的学生虽然是第一次接触折线统计图, 但是对于“统计图概念”并不陌生, 因为在此之前, 他们已经学习了统计表与条形统计图, 并经历过简单数据的搜集、整理、描述、分析、判断等过程。基于学生的学习起点, 在教学的开始环节, 笔者从统计现实生活中私家车的话题入手。
首先, 让学生观察笔者在上班途中拍摄的小轿车拥挤不堪的图片, 谈谈自己的感受。当他们说出“现在的车真多啊”“人们的生活富裕了”“购买私家车的人家越来越多了”之后, 追问:“看到这样的情形, 你想了解一下我县近几年来小轿车数量的整体变化情况吗?”大家齐声说:“想!”这样, 让学生通过观察图片、联系生活实际, 引发出统计本县近几年小轿车数量变化情况的愿望, 激发了他们的学习需求;接着追问:“要想了解我县近几年来小轿车数量的整体变化情况, 首先要做些什么?”唤醒学生对已有知识的回忆, 知道要进行统计, 搜集数据是第一步;然后, 笔者出示了“2012年—2016年我县购买小轿车的数据”, 进一步启发:“我们可以怎样整理它呢?”引导学生利用已学过的统计表与条形统计图等知识进行统计与整理, 并对统计的结果进行简单的分析比较, 知道在这里条形统计图可以更直观地看出小轿车数量的多少;最后, 笔者继续追问:“在条形统计图的基础上能不能再进一步进行整理, 使它更简洁些呢?”这样, 通过设计一系列的认知冲突, 在不断激发学生认知需求中, 将他们的思维一步步引向深入。
二、在直观抽象中感悟数学思想
数学思想是指现实世界的空间形式和数量关系反映到人们的意识之中, 经过思维活动而产生的结果, 它是数学核心素养的重要组成部分。在折线统计图的教学中渗透“转化、对应、函数”等数学思想, 能很好促进学生数学核心素养的提升。
由于“折线统计图”这个概念的文字叙述比较抽象, 在教学中, 可以根据新旧知识之间的联系, 借助多媒体的动态演示, 把已学习的条形统计图演变成折线统计图, 直观地呈现出条形统计图与折线统计图之间的联系。学生在看得见、摸得着的思考过程中进一步体会到:两个有联系的知识可以建模成新的知识, 而这个新的知识也可以为下一次建模提供必要的条件, 他们对数学知识之间的联系有了更为深刻的理解。
课堂上, 笔者首先启发学生进行大胆猜想:“怎样才能使条形统计图更简洁些呢?”学生经过一阵激烈的讨论之后, 纷纷举手阐述自己的想法。有的说可以把直条画细一些, 有的说可以把直条由底往上缩小, 一直缩到只保留最上面的一横条, 还有的说可以把直条由底往上缩小变成一个点等等。笔者首先肯定了大家的各种想法, 接着利用多媒体进行动态演示, 先将条形统计图中的直条由底往上缩, 最后变成与之一一对应的简单的小点, 并让学生说说这些点表示什么意思。然后, 利用动画演示, 顺次连接每个点, 形成折线统计图, 引导学生发现这些点连成的线段之间的区别, 从而引出折线统计图的特点, 即根据线的变化能直观地看出数量的变化。在此基础上, 笔者指出:像这样顺次把两点连接起来的曲折变化的线叫做折线, 这样的统计图我们把它叫做“折线统计图”。通过一系列有效的操作活动, 学生不仅形象直观地理解了折线统计图的概念, 而且在活动中真真切切地加深了“一一对应”“函数”和“转化”等数学思想的理解。
三、在数据分析中提升理解能力
数据分析是统计教学的一个重要任务。通过引导学生对所搜集的数据进行简单的分析, 从中提取出有价值的信息, 不仅能使学生感受到数据分析的意义和作用, 帮助学生积累数据分析经验, 而且有利于培养学生的数据分析能力, 使学生在学习的过程中逐步学会如何根据统计结果做出简单的分析、判断和预测, 为学生的后续学习奠定更为坚实的基础。
教学中, 在揭示折线统计图的概念之后, 笔者重点引导学生对图中的数据进行分析。第一, 说一说从图中可以看出在相邻的两个年份中, 哪两年中小轿车数量增长得最快?最慢呢?你是怎么知道的?当学生说出“相邻两个年份之间的线越长, 小轿车的数量增长得越快”这个结论时, 教师追问:“还有不同的看法吗?”从而引出“还可以从线的倾斜角度看, 线的倾斜角度越大, 表示小轿车的数量增长越快, 反之则慢。”笔者并没有到此为止, 而是继续追问:“你还能想到不同的方法吗?”引出计算的方法, 并在三种方法的比较中进一步看出:从线的长短或线的倾斜角度进行分析这两种方法比较简单。第二, 说一说小轿车数量的整体变化情况。当学生得出“小轿车的数量整体上是呈上升趋势的”结论之后, 笔者引导他们继续思考:这种趋势说明了什么?启发学生透过现象看到问题的本质。第三, 根据这种整体的变化, 预测一下2017年全县小轿车的数量。适时地对学生进行“少开私家车, 尽量选择环保交通工具出行”等方面的人文思想的渗透。通过引导学生经历数据分析和根据图中的数据进行简单的预测的过程, 在潜移默化中培养了学生的数据分析能力。
四、在回顾反思中建构认知系统
数学知识之间是有联系的。数学教学中, 充分挖掘新旧知识间的内在联系, 将所学的新知识纳入到已有的旧知识之中, 从而将零散的数学知识连成一片, 形成知识网, 能很好地帮助学生建构认知系统。
教学中, 笔者在新课结束后, 重点引导学生就几个问题对本节课的学习过程进行回顾与反思:第一, 说一说我们今天学习的折线统计图是怎么得到的?第二, 折线统计图和条形统计图有什么区别与联系?第三, 条形统计图变成折线统计图后有什么优势?通过问题, 引导学生进行有重点的回顾与反思, 使学生逐步明晰折线统计图是在条形统计图的基础上发展变化而来的, 它比条形统计图更加简洁。条形统计图变成折线统计图之后, 不但能看出数量的多少, 还能清楚地表明数量的增减变化情况, 便于比较。这样的教学, 有效地沟通了数学知识间的联系, 不仅有助于学生认知系统的形成, 而且能使学生进一步明白:数学知识之间都是有联系的, 在遇到新的问题时, 可以根据这种联系, 把它转化为已学过的旧知识进行解答, 从而为学生的后续学习打开了另一扇窗。
五、在解决问题中发展学生智慧
怀海特先生认为:“知识的重要性在于它的运用, 在于我们对它能动的掌握——也就是说, 在于智慧。”智慧是对事物能够迅速、灵活、正确地理解和处理的能力, 而知识只是追求智慧过程中的阶段性产品和部分产品, 并不是智慧本身。因此, 教师必须把教学知识与发展学生智慧和谐地统一起来, 着力培养学生灵活运用知识解决实际问题的能力。在本课的教学中, 笔者设计了如下的练习:
1. 连一连。
选择合适的统计图, 并说一说你是怎样想的)
李红6—10岁身高变化情况统计图
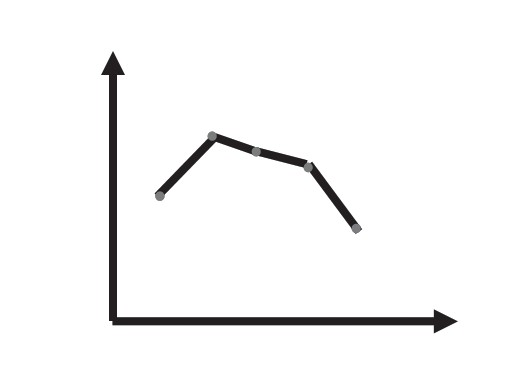
亚洲五个国家人口情况统计图
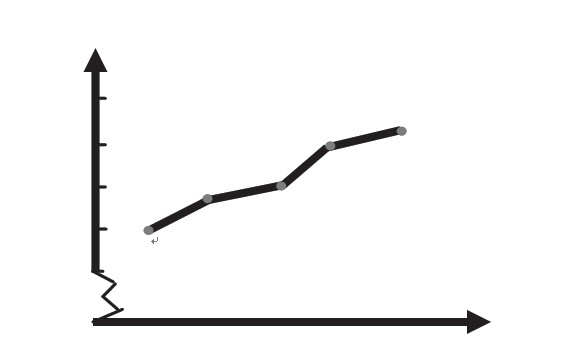
张华家今年前5个月电费情况统计图
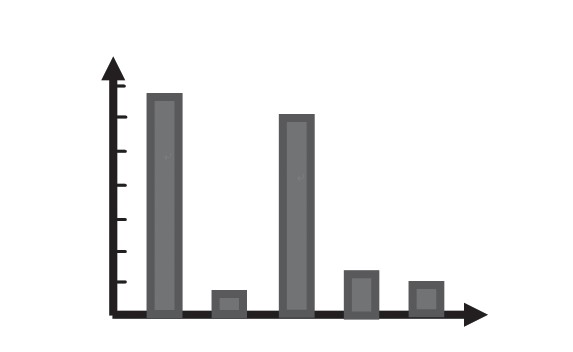
2. 产品推销。
(请你帮陈经理想办法)
A:我们的产品在2012年的销售量就突破了500万台, 选我们A品牌的冰箱吧!B:我们B品牌的冰箱, 在2014年的销售量就突破了500万台, 选我们的货吧!陈经理:到底选哪家的货呢?
辨析的过程就是提升经验、建构模型的过程, 也是学生灵活运用知识解决实际问题的过程。在前面的教学活动中, 学生通过学习已经掌握了折线统计图的特点, 并了解了折线统计图与条形统计图的区别与联系, 积累了解决问题的经验。在此基础上, 笔者侧重于引导学生对经验进行提升, 通过对“选择合适的统计图, 连一连”与“产品推销”等问题的解决, 进一步巩固他们对条形统计图与折线统计图特点的认知。根据实际需求, 学会正确地选择合适的统计图, 同时也使学生明白:用数学知识可以创造性地解决生活中的实际问题, 加强了数学与生活的联系, 进一步体会到了学习数学的价值, 提高了运用数学知识解决实际问题的能力, 发展了智慧, 学生的数学核心素养因此而自然生长起来。





