
针对高中数学教学,新课标要求教师必须重视数学思想方法的应用,引导学生对数学中存在的问题进行分析与解决。将教材及资料中的化归思想方法充分地挖掘出来,提升学生解决问题的能力。
一、化归思想方法的概述
所谓化归,指的是"转化"与"归纳".其思想模式通常为:问题-新问题-解决新问题-解决原问题。从哲学上来看,这种思想方法着眼于迁移转化,通过揭示问题之间的联系,从而实现问题的转化,使问题进一步规范化.
化归思想的特征有:层次性、重复性、多向性。为了使化归条件能够有效实施,在问题解决过程中可以变换问题的条件,同时还能够变换问题的结论,将问题的内部结构与外部形式进行改变,体现了化归的多向性特征。化归思想的重复性特征主要表现为其能够调动各种方法与技术,从微观上解决较多的问题,同时从宏观上能够实现学科之间的转化.
二、高中数学教学中对化归思想教学法的应用
(一)化归思想在高中数学基础知识教学中的应用
高中数学的基础知识教学也属于解方程教学,在方程式的解答过程中,利用化归思想可以将复杂的方程式转化为简单的方程式。例如,在解决三元一次方程组时,为使其能够简单化,可以先将其转化为二元一次方程组,最后再经过转化使其成为一元一次方程式。在课堂教学准备阶段,教师应该做好教材内容解析教案,并且按照化归思想的解决目的将数学知识中的化归过程整理出来,才能够满足课堂教学要求。
对于化归思路的整理应该适应学生掌握化归思想的步调,这样就可以促进学生从更高的层次上掌握化归思想的目标。如图 1 所示。
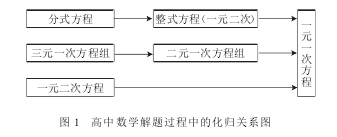
该图揭示了化归思想在高中数学解题中应用的本质,教师就是利用这张图在高中数学教学中来培养学生的主动性及运用化归思想解决问题的能力.
(二)化归思想在高中数学解题教学中的应用
近年来,化归思想在高中数学解题教学中已经得到普及,并且取得了较多的成果.
但是,从整体应用上来看,这种思想的应用还存在一定的缺陷。例如,在方程式的解答中,对于一元二次方程式,很多教师整合不同方程式之间解决问题的化归关系,最终使得学生难以分清一元二次方程式与其他类型方程式之间的关系。学生用化归思想解决数学问题在理解层面上就有困难,从而阻碍了教学的顺利进行。高中学生在学习数学的过程中往往会陷于无目标的盲目状态,但是,教学要求学生利用简单的知识来解决复杂的问题,因此,教师在讲解化归思想的过程中,应该从问题的侧面进行点拨和讲解。
例如,在三元二次方程式 x3+(1 + 2姨)x2-2=0 的讲解中,首先仔细观察方程,从中可以发现方程中有含有 2 的两个数字,可以想到关于姨2的一元二次方程,可以在解方程的过程中先将x 看做常数,只要求算出方程的解就能够求出未知数x 的解。为此,可以将原方程化为( 2姨)2- 姨 2x2-(x3+x2)=0,解出两个关于 x 的解,分别是 2姨 =-x与姨 2= x2+x,从而能够得出原方程的解.
此外,化归思想还能用于直线与平面平行的判定教学中以及梯形面积与定积分等教学中,无论是哪一种教学过程,要想确保化归的有效性,就需要设定明确的化归目标,只有在既定的目标下才能够找到化归的途径,在解决途径的引导下将问题简化,此过程中需要实施者保持清晰的思考,不盲目实施解题步骤才能够避免错误的解答。当然,化归思想也不是能够保证所有问题的解决,它是以数学发现为基础,因此,在解决数学问题的过程中不能任何问题都用化归思想,应该保持与时俱进的精神,想到解决办法。
综上所述,对于高中数学教学而言,化归能力的提升一定程度上能够解决高中数学中的关键问题,是高中数学教学水平提升的前提与保障.因此,教师应该在化归思想教学中加强努力,从多角度进行课堂教学,为学生创设一个趣味性的学习平台,鼓励学生触类旁通,帮助学生学会善于利用化归思想发现和观察问题,并且能够通过类比的方法很好地解决数学中的更多问题,避免学生在解决问题中走更多的弯路.
参考文献:
[1] 田文亭。化归思想在高中数学中的有效运用及探讨[J].试题与研究:新课程论坛,2014(27):47.
[2]周炎龙.化归思想在高中数学中的体现和教学[D].新乡:河南师范大学,2013.
[3]刘芳.谈化归思想在高中数学教学中的运用[J].课程教育研究:新教师教学,2014(15):124-125.
[4] 朱爱明。谈高中数学中的化归思想[J].中学生数理化:学研版,2014(10):44.





