
一、引言
PISA 是经济合作与发展组织( Organization for Economic Co - operation andDevelopment) 举办的对在校学生的技能和知识状况的国际性评价计划。在全球七十个多国家或地区举办,评价对象是即将完成义务教育的,年龄在 15 岁左右的在校学生。
PISA 的测试领域为阅读、数学、科学等。PISA 旨在评估学生在各领域的素养,以创新的方式反映与成人生活有关的技能的判断,为政策对话和制定、实施教育目标的合作提供基础。PISA 代表了发达国家对教育的基本理解和要求。
对 PISA 的考试目标,能力要求,评分细则等进行研究可以发现得到许多有意思的结论,例如庞维国等对家庭社会经济地位与中学生学业成绩的关系进行了研究。
因此 PISA 受到了各国的重视,本文则是将 PISA 测试与高考进行了比较研究。
高考是我国高校录取新生的主要形式,同时对中学教学具有一定的导向和评价作用。因此关于 PISA 与高考在考查目的和考查效度方面的对比研究,对研究高考的目的、改进高考命题具有借鉴意义。本研究抽取了河北、海南、云南等 10 个省( 区、市) 的四千余名考生,首先采集其 PISA 测试的数学成绩,待其参加高考后再采集其高考数学成绩,然后进行对比分析和研究。
二、PISA 数学与高考数学的考查目标分析
( 一) PISA 数学素养的界定
PISA 测试中对数学素养的定义是: 数学素养是鉴别和理解数学在现实世界中的作用的个人能力,做出有理有据的数学判断的个人能力,以及作为一个有独创精神、关心社会、善于思考的公民利用数学并参与其中以满足个人生活中各种需要的那种能力。
PISA 从广阔的内容区域中选取数学内容,评价是围绕四个内容区域确定的:
空间与形状: 涉及空间与形状的现象及关系,它通常要利用几何课程学科。它要求在分析形状的组成部分以及在不同的表述和不同的大小中识别各种形状时寻找相似或不同,以及理解对象及其相关位置的特征。
变化与关系: 涉及各种变化的数学表现以及各种变量间的功能性关系及其附属关系。这一内容区域与代数的关系最为紧密。数学关系通常以方程或不等式表示,但更为普通的性质( 这里仅举几例: 等值、整除性以及包含) 的关系同样有意义。各种联系采用不同的表示,包括符号的、代数的、图形的、表格的以及几何的表示。由于不同的表示可能用于不同的目的并具有不同的性质,在处理各种情况和任务时,各种表示之间的转换往往至关重要。
数量: 涉及数字现象、数量关系及模式。它关系到相对量的理解、数字模式的识别以及用数字表示真实世界对象( 计算与测量) 的数量及可量化的特征。另外,数量还涉及不同方式表示的数字加工和理解。处理数量的一个重要方面是定量推理,它涉及数感、数字的表示、对运算的含义的理解、心算以及估计。与定量推理相关的最基础的数学课程分支是算术。
不确定性: 涉及概率与统计的现象与关系,在信息社会中,它们的意义日益重要。这些现象是统计与概率中的数学研究的对象。
( 二) 高考数学能力要求
高考数学能力成分含义:
( 1) 逻辑思维能力: 会对问题或资料进行观察、比较、分析、综合、抽象与概括; 会用演绎、归纳和类比进行推理; 能准确、清晰、有条理地进行表述。
( 2) 运算求解能力: 会根据法则、公式进行正确运算、变形和数据处理; 能根据问题的条件,寻找与设计合理、简捷的运算途径; 能根据要求对数据进行估计和近似计算。
( 3) 空间想象能力: 能根据条件做出正确的图形,根据图形想象出直观形象; 能正确地分析出图形中的基本元素及其相互关系; 能对图形进行分解、组合;会运用图形与图表等手段形象地揭示问题的本质。( 4) 数据处理能力: 会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息,并作出判断; 应用统计或统计案例中的方法对数据进行整理、分析,并解决实际问题。
( 5) 创新应用能力: 能发现问题、提出问题,综合与灵活地应用所学的数学知识、思想方法,选择有效的方法和手段分析信息,进行独立的思考、探索和研究,提出解决问题的思路,创造性地解决问题,包括解决相关学科、生产、生活中的简单数学问题。
( 三) 测试目标对比研究
通过对比、分析 PISA 数学与高考数学的测试目标,可以看出:
( 1) PISA 虽然是以数学内容的特点划分考查的子模块,但其中并没有标明具体的测试内容,而是以对内容的操作方式和处理程度作为主要内容,事实上是具有数学内容特点的能力要求。例如在“数量”部分,其要求对相对量的理解、对数字模型的识别以及用数字刻化物质对象的特征,同时还要求定量推理、心算、估算等。
( 2) PISA 对各部分内容的要求与高考的能力要求类似或相近。以“空间与形状”为例,将 PISA 所要求的对图形的操作、寻找关系和表述关系等与高考数学中界定的空间想象能力相比较,可以看出其中的相同或相近。【表】
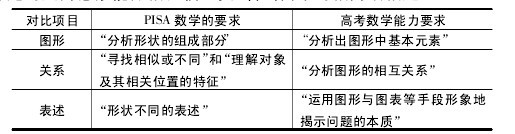
进一步的分析可以看出,其空间与形状和空间想象能力对应,变化与关系和逻辑思维能力对应,数量和运算求解能力对应,不确定性和数据处理能力对应。而高考中要求的创新应用能力和 PISA 的总体要求相类似。
( 3) PISA 和高考的要求反映了数学测试的基本目的和要求。数学由于高度的抽象性、结论的确定性和应用的广泛性的特点,在社会生产生活和人类思维训练中发挥重要作用。就其社会效用而言,数学是研究空间形式和数量关系的科学,是刻画自然规律和社会规律的科学语言和有效工具。数学科学是自然科学、技术科学等科学的基础,并在经济科学、社会科学、人文科学的发展中发挥着越来越大的作用。
数学在人的培养和发展中也发挥着独特的作用,它促进人类理性思维和个人智力的发展,是人类文化的重要组成部分。数学素养是公民所必须具备的一种基本素质,它为学生的终身发展,形成科学的世界观、价值观奠定基础,对提高全民族素质具有重要意义。因此数学测试在选拔考试中发挥基础学科的重要作用,一方面检验学生是否具备解决问题的知识基础和工具,另一方面检测学生是否具备学习和生活的能力。
由于数学学科的基础性,各国的入学考试几乎都考数学,各国的考试都对数学提出了普遍性的要求。数学考试一方面考查学生掌握数学的基础知识、基本技能、基本思想和基本活动经验; 同时更加注重对学生能力方面的要求,考查计算能力、理解和表达能力、推理能力、论证能力和解决问题的能力,还要求学生表达清晰、思考有条理,用科学的思考方式解决问题、认识世界。这些都是学生能力的重要内涵和表现形式,数学学科由于其对能力考查的通用性,在潜能甄别方面发挥重要作用。
三、PISA 数学与高考数学的考查效度分析
( 一) 相关分析
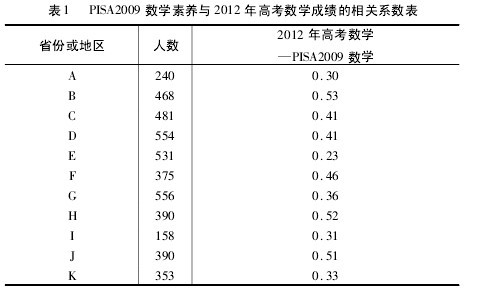
通过对 PISA2009 中国试测研究各试点省份或地区 2009 年高一年级 4496名考生数学成绩和同一批人 2012 年高三高考数学成绩追踪匹配后的相关分析,得到各试点省分群体的相关系数。表 1 是分省的统计数据,字母为各省代码,可以看出,各省的相关系数多数都在 0. 3 上,说明 PISA2009 数学成绩和 2012 年高考数学成绩的相关较高,其中 B、C、H、J 等省的相关系数更高,而 I、K 省的相关系数相对较低。由于目前高考实行分省命题,各省的数学试题具有一定的差异性,但能力考查要求是由全国统一的考试大纲确定的。此处的相关系数虽然不能直接进行比较来说明省际之间的优劣,但仍旧在很大程度上反映了这两个考试的内在联系。【表1】
( 二) 排名对比分析
在此,我们以某省为例进行,先将某省参与抽样的 24 所中学中每个中学参加 PISA 测试的数学成绩进行平均,得出该学校 PISA 数学成绩在全省的排名; 然后类似,将这些考生的高考数学成绩进行平均,得出该学校高考数学平均成绩在全省的排名。
从表 2 可以看出,在抽样的 24 所学校中,各学校在两种考试之间的差异度大概分为四个层次: 名次差异在 0 ~1 之间的学校数量为 50%; 名次差异在 2 ~3之间的学校数量为 21%; 名次差异在 4 ~5 之间的学校数量为 17%; 差异在 5 个名次以上的学校数量为 13%。该省学校在两种考试之间的名次波动较小,表明其在这两种考试上的表现基本一致。【表2】
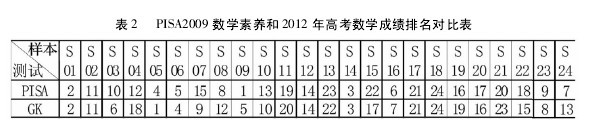
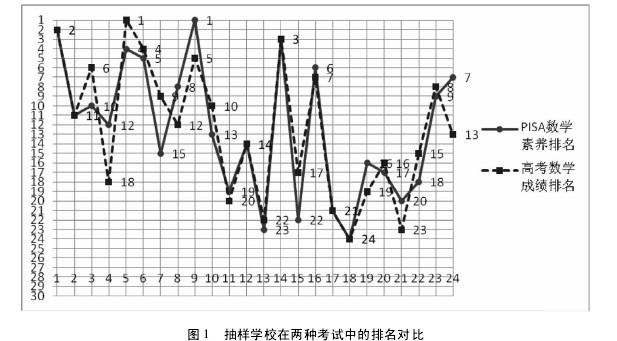
图 1 中,横轴表示匹配的抽样学校的编号( SCH1 - SCH24) ,纵轴表示该学校在 24 所抽样学校中的排名,实线代表 PISA 数学成绩排名,虚线代表高考数学成绩排名。从图中可以看出,代表 PISA 数学成绩排名的曲线和代表高考数学成绩排名的曲线非常的相似,呈现出了较高的一致性。【图1】
( 三) Kendall 协调系数 W 检验
前面利用描述性统计的方法分析了同批次学生在 PISA2009 数学素养和2012 年高考数学两种不同考试上的表现。由于 PISA 测试与高考测试是两种不同的考试评价方式,在测评结果的报告方式上有着很大的不同,传统的参数检验方法难以对两种测试的一致性进行分析,为更加细致的检验两种考试对考生评价结果的一致性,评估两种考试的考查效度,我们采用 Kendall 协调系数 W 检验方法来进行研究。
在研究工作中需要按照某些性质两次或者更多次的对被评价个体进行评估( 通常表现为一定的数值或者次序) ,要考查这些评价结果的一致性显得尤为重要,Kendall 协调系数 W 检验方法是表示多列等级变量相关程度的一种非参数检验方法,适用于两列以上等级变量。Kendall 协调系数 W 检验方法的零假设为: 两种或者多种评价方式之间是不相关的; 备选假设则为: 这些评价方式对个体的评价在特定显着水平下是有一定相关性的。具体分析如下:( 1) 对 PISA 测试和高考测试按照学校个体的评价结果进行秩( 排序) 转换,参考表 2。
( 2) 该问题由两个区组构成,共有 24 个被评分个体。检验假设的零假设为: PISA 测试与高考测试之间没有明显的一致性; 备选假设为: 两种测试存在明显的一致性。显着性水平假设为 α =0. 05。
( 3) Kendall 协调系数 W 的统计量描述为:【公式】
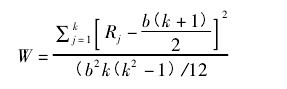
其中,b 表示区组的个数,k 表示被评价个体的数量,Rj为第 j 个被评价个体在不同区组中的秩次之和。在被试数量较少时,通过通用的 Kendall 系数表即可以根据 W 值来判断结果的显着性,当被试数量较大时,一般认为该统计量的变换近似有如下分布形式:b( k - 1) W ~ χ2( k -1)并由卡方界值表或者统计软件可以判断结果的显着性。
在该研究中,b =2,k =24,W 值的自由度为 23,则根据 W 的计算公式,计算得到的 W 值为: 0. 95,b( k -1) W =43. 7。根据卡方界值表得到临界值 35. 17 <43. 7,则 P < 0. 05,在显着性水平 α = 0. 05 下,拒绝零假设,接收备选假设。
( 4) 结论: 通过 Kendall 协调系数 W 检验方法,PISA2012 数学素养和中国2012 年高考数学成绩在( α = 0. 05) 显着条件下有着显着的一致性,所以这两种测验方法在数学能力的考查和评估结果上较为相似,有着较高的效度。
四、结语
( 1) PISA 的数学测试和高考数学考试,虽然测试的内容不同,但测试目的相近或类似。社会生产生活的各个行业虽然专业不同,但对数学的需求有共通之处,一方面是对一般公民的数学素养的需求,另一方面是应用数学工具解决实际问题的需求。所以无论是 PISA 还是高考数学考试在检测过程中都力图反映社会需求,发挥两方面的作用,一是作为思维的工具和甄别思维能力的材料,考查考生思维和推理能力,二是作为解决问题的工具,考查考生掌握数学知识的广度和深度,应用数学知识分析、解决数学问题和相关学科问题的能力。
( 2) PISA 和高考数学测试反映了数学作为学习和研究现代科学技术必不可少的基本工具,数学测试具有稳定、有效的特点,受地区差异和文化差异的影响较小,甚至受到考查年限的跨度和考查具体数学内容的影响也较小。
( 3) PISA 和高考中的数学测试反映了数学测试的基本要求和在鉴别学生中的基础作用,在考生的评估和甄选中都发挥重要的作用。PISA 和高考中的数学测试反映了在数学能力考查上,虽然命题的形式有所不同,但评价结果仍有较高一致性,考查效果高度相关。( 4) 本研究的数据分析部分只是对 PISA2009 数学成绩和 2012 年高考数学成绩的相关的统计分析,虽然人数较多,但只是一次的统计数据,因此得出的一些结论不排除受到偶然因素和统计分析方法的影响,所以还需要更多的数据分析证据支持已有的结论。
参考文献:
[1]亓永平. PISA: 全球性学生素质评价[J]. 全球教育展望,2002( 10) : 59.
[2]The Organization for Economic Co - operation and Development ( OECD) . OECD Programme for InternationalStudent Assessment ( PISA) [EB / OL].
[3]庞维国等. 家庭社会经济地位与中学生学业成绩的关系研究[J]. 全球教育展望,2013( 2) : 12 -21.
[4]Wayne. W. Daniel,Applied nonparametric statistics[J]. 2th edition. Boston: PWS - KENT Publishing Com-pany. 1990.
[5]王蕾. 教育评价探新[M]. 西安: 西安交通大学出版社,2007.





