摘 要: 思维导图的重要理论依据是脑科学, 而思维导图在高中数学课堂教学中的应用比较广泛, 能够用最直观形象的形式把抽象、复杂的数学知识直观地展现在学生面前, 让各个知识点之间相互联系起来, 不断完善学生的数学知识结构, 思维导图的应用能够培养学生优秀的逻辑性思维能力与抽象性思维能力, 拥有较强的学科核心素养, 从而能够对所学到的数学知识有较为透彻的理解与认知, 做到学以致用、融会贯通。
关键词: 思维导图; 高中数学; 教学方法;

一、在高中数学课堂教学中应用思维导图的可行性
1. 符合高中数学课程的特点
在新课程标准下, 教师不仅仅要教会学生理论知识与应用技能, 更重要的是要让学生关注数学知识的应用与数学历史背景, 从而能够加深对所学知识地理解和记忆。数学知识关系着人类文明、社会地进步与发展, 学生在学习数学概念的时候, 首先要了解出现数学概念的历史背景与应用范围, 思维导图能够完美诠释数学概念。其次, 高中数学知识较为抽象、逻辑性比较严谨、任务量较大, 学生想要对所学到的数学知识有较为透彻的理解与认知, 需要具备较强的数学思维能力, 而思维导图能够把抽象数学知识简单化、形象化, 减轻学生的学习压力, 构建完整的数学知识体系。
2. 适合高中生学习数学的特点
高中生相对于初中生、小学生拥有较强的生活经验与科学知识, 所以能够更好地理解各个学科之间的内在联系, 学生在分析、观察学科规律之后, 可以大胆提出假设与猜想, 并且利用实例来验证自己的猜想与假设, 高中生更多的是关注未来, 不仅仅是立足在眼前。高中生在数学思维能力上拥有较强的自我监督性, 可以寻求更高的学习效率, 时刻进行自我反省。最后高中生的数学思维在逐渐完善, 并且趋于稳定, 而以上高中生学习特点都是能够让思维导图更为巧妙的导入到高中数学教学中去, 具备较强的可行性与有效性。
二、思维导图的基本特征

从上面那个图片可以很明显的看出思维导图的特征, 思维导图的中心部分是整个图片所要表达的重点内容, 各个分支是有中心部分发散出来的。思维导图整体呈现出树状分布结构, 并且由各个分支组成的节点结构。思维导图的中心部分一定是图片, 因为大脑总是对图片的记忆比较深刻, 图片的表达形式比较直观和简单, 其次, 思维导图虽然整体呈现的是树状结构, 但是每一个分支上都会有相应的解释性的关键词, 从而来体现中心思想。
在高中数学课堂教学中应用思维导图, 能够结合学生的已有数学知识水平和最近发展区, 来模拟出数学知识的思维示意图。这样既能够培养学生优秀的数学思维能力, 又能够让学生利用所学数学知识来解决实际生活问题。思维导图是数学教师和学生之间思维的“火花”, 思维导图的应用是一种境界, 也是一种科学, 更是艺术的精髓。
三、思维导图地绘制方式
思维导图地绘制方式包含了传统地绘制方式、计算机绘制方式。传统地绘制方式是在教室板书、白纸上开展人工手绘, 从而提取出关键的数学主题, 这是针对比较简单的数学知识, 而计算机绘制方式是针对教学内容较为复杂的数学知识, 如果采用传统地绘制方式会浪费大量的数学课堂时间和精力, 而计算机技术较为便捷, 教师可以利用利用计算机来绘制思维导图, 计算机思维导入更加注重字体形式、颜色、大小等, 更为直观的把思维导图呈现在学生面前。
四、思维导图在高中数学课堂教学中的应用方法
1. 利用思维导图来解决重点教学问题
并不是所有的高中数学知识都适用于思维导图, 一些简单的数学概念、原理采用传统的数学教学方法就可以, 而对于高考的压轴题、难点数学题可以利用思维导图来提高数学课堂教学的有效性, 帮助学生更好地理解数学问题。例如, 导数就是高中数学课堂教学中的重点教学内容, 在数学考试中教师往往会把导数与函数联系在一起考, 称之为导函数, 导数属于导函数中的特例情况, 导函数往往都是需要利用图像来解决问题, 所以思维导图在导数教学中的应用是非常有必要的。教师可以设定以下导数的思维导图, 开展自上而下的数学教学层次, 让学生在学习过程中有过渡时间, 从而更好地理解导数教学内容。 (下转第73页)
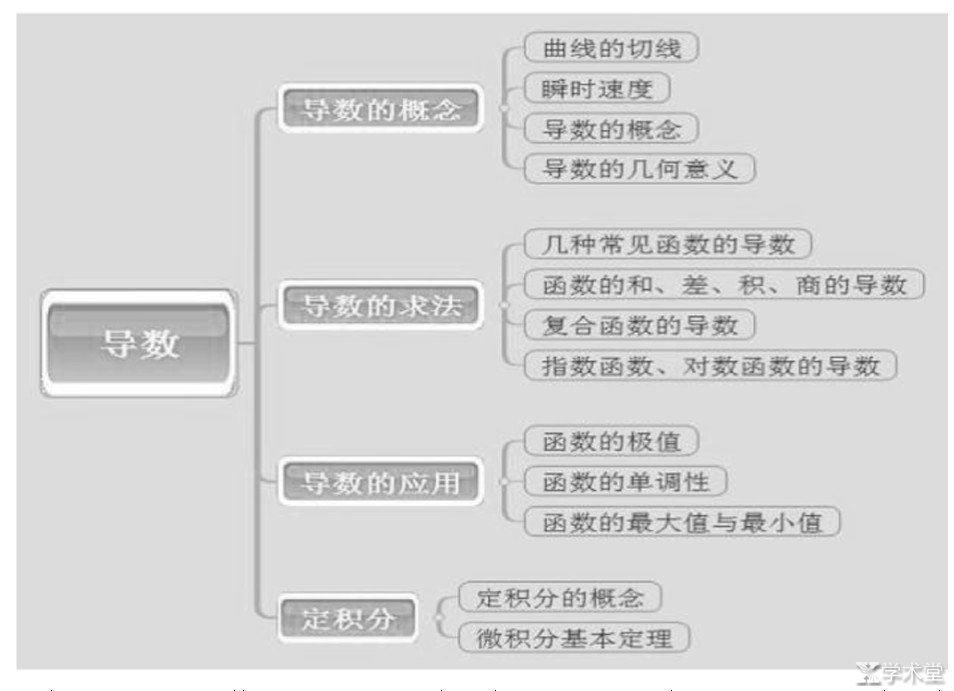
教师要先讲解导数的概念, 让学生对函数的概念有足够地了解, 然后再开始导数求法教学, 让学生去了解较为常见的函数的导数, 能够充分理解函数的和差积商的导数与复合函数求导的法则, 最后是导数的具体应用, 让学生明白可以利用导数做什么, 然后让学生去观察函数的图像, 单调递增、单调递减、波峰波谷等三个部分。思维导图在高中导数课堂应用过程中教师要加强和学生之间的沟通与交流, 提高学生的注意力, 让学生脑海中有清晰、完整的导数知识结构。
2. 利用思维导图开展高中数学复习工作
高中数学知识量比较多、难度较大, 学生存在较大的高考压力, 所以高考复习对于学生来讲是非常重要的, 教师要充分利用思维导图来开展高中数学复习工作, 充分提高高中数学工作的效率与质量, 让学生能够取得一个理想的数学高考成绩。例如, 在开展余弦定理的整理与复习教学工作的时候, 教师可以给出以下思维导图开展数学复习。
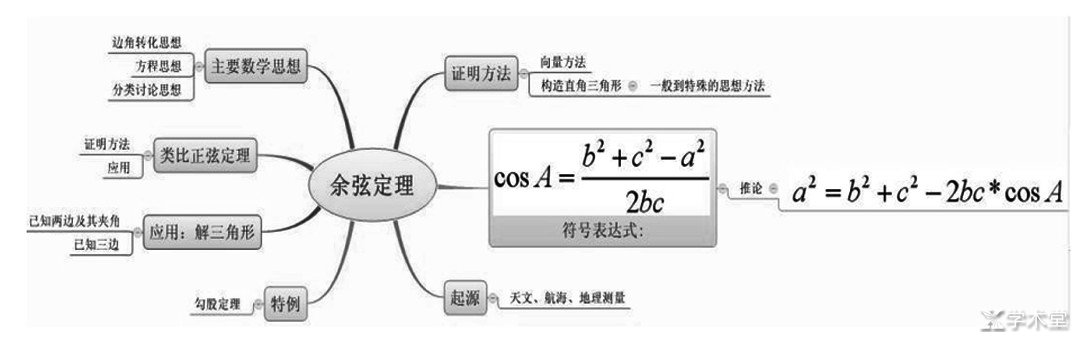
教师和学生按照图片分支结构开展复习, 让复习工作能够井然有序地进行下去。“余弦定理”是“解三角形”中的重要定理, 并且在地理、航海、天文测量中都发挥着重要的作用, 主要是表达三角形角、边之间的关系。由上面的思维导图可以得到需要重点复习的数学知识点, 了解三角形的三条边长, 可以求得三个内角, 了解三角形的夹角与两边, 能够求得第三边, 了解三角形一边对角与两边, 能够求得第三条边与其他的角。其次, 利用余弦定理能够判断角是钝角、直角, 还是锐角, 推算出向量的数量积运算。通过思维导图能够深入理解各个知识点之间的共同之处与不同之处。
3. 利用思维导图来开展合理的教学评价
思维导图也能够检查学生对所学知识的掌握程度, 教师可以在本堂课结束之后, 让学生结合所学到的数学知识来绘制思维导图, 教师可以通过每一个学生的思维导图来评价学生的整体认知结构, 充分了解学生真实的学习进度与需求, 从而及时的调整数学教学方案与目标, 让每一个学生都能够跟得上数学课堂教学的进度, 并且透彻掌握每一个数学知识点, 做到学以致用、融会贯通。
总之, 在高中数学课堂教学中, 教师要把思维导图的作用、优势充分体现出来, 利用思维导图让学生拥有完整的数学知识结构, 培养学生优秀的数学素养。
参考文献:
[1]李琳, 陆万顺, 李星.思维导图应用于培养创新思维有效性的研究——以高中生数学创新思维的培养为例[J].宁夏师范学院学报, 2018, (01) :82.
[2]王艳丽.思维导图在高职院校课后学习《高等数学》中的应用探究[J].科技经济导刊, 2017, (26) :176.
[3]权国龙, 顾小清, 姚媛媛, 龚晋瑜.图解的设计与应用——可视技术辅助数学应用解答之行动研究[J].电化教育研究, 2017, (02) :112.





