摘 要: 数学复习是巩固知识、强化学习的过程, 要求开放式多元化学习空间的创设, 促进有效学习的生成。“一题多变”思想能够实现知识的汇总、串联, 也为知识的拓展应用, 搭建了良好条件。本文从高中生的学习视角出发, 就如何提高数学复习效率, 提出了几点建议, 促进学生有效学习。
关键词: 高中数学; 一题多变; 复习; 实践;

Abstract: Mathematics review is a process of consolidating knowledge and strengthening learning. It requires the creation of an open and diversified learning space to promote the generation of effective learning. The idea of "problems with variations" can realize the aggregation and concatenation of knowledge, and also builds good conditions for the application of knowledge. From the perspective of senior high school students' learning, this paper puts forward some suggestions on how to improve the efficiency of mathematics review, so as to promote effective learning.
Keyword: senior mathematics; problems with variations; review; practice;
1、 前言
数学是高中课程体系中的核心课程, 是培养核心素养的重要载体。作为高中生, 在数学知识的学习中, 应强化对知识的理解与应用, 提高数学学习能力。在数学复习中, 学习思维的转变尤为重要, 要突破僵化的学习模式, 在一题多变的思想之下, 通过知识的归纳、汇总及拓展, 进一步促进知识内化。高中生思维活跃, 一题多变的思想更加契合学生的思维模式, 也有助于核心素养的培养。因此, 高中生在数学复习中, 要立足基础知识, 理解并吃透, 转变传统复习模式, 以实现有效数学学习。本文基于学习经验, 以复习学习为例, 就如何提高复习效率, 做了具体阐述。
2、 从“变”中扎实基础, 促进知识深入理解
数学知识的有效学习, 关键在于强化基础知识的理解, 为知识的系统构建创设良好的复习条件。课本习题以基础练习为基础, 要求吃透基础知识, 并在由简到难的深入学习中, 进一步促进知识的归纳、拓展进而促进有效学习的实现。在学习中发现, 由基础知识演变而来的数学习题, 更加注重复习中从“变”抓住要点, 在枯燥、单一的数学知识中, 寻找“新”的知识点, 让数学学习更加丰富多彩, 而不是局限于课本知识的学习。因此, 一题多变的数学实现, 就是要变“中”扎实基础知识的学习, 让复习更加“固本开源”, 能够进一步促进对教材知识的深入理解, 这是有效复习的关键。
等比数列是高中数学课程的重要内容, 其学习的难点在于如何依托基础知识的变形, 实现快速有效的通项公式求算, 这是等比数列复习的重中之重。不同的变式, 要求学生对构造方法的灵活应用, 形成良好的知识体系。
例:数列{an}中, 已知a1=1, 且an+1=2an+1, 求{an}通项式。
该题只需要运用等比数列的基础知识便可以快速解答, 该题目的复习点, 在于强化对基础知识的识记和理解。但真正的复习不能停留于此, 而是需要在变式中, 实现对知识的“多样化”应用, 掌握如何构建新的等比数列, 是深入知识理解, 提高复习效率及质量的重要切入口。为此, 该题目往往会进行变式, 从简到难, 从基础点到拓展面, 都是数学复习的常用技巧, 能够更好地归纳与总结知识点。
变式1:数列{an}中, 已知a1=1, 且an+1=2an+n, 求{an}通项式。
相比于原题, 变式1将“加上常数”变式为“加上变量”。变量“n”的出现, 提高了题目的难度, 要求学生在对常规基础知识的应用中, 能够懂得适当的变形, 转变思维切入点, 以构建数列的思维模式, 实现对通项式的求算。
变式2:数列{an}中, a1=1, 且an+1=2an+2n+1, 求{an}通项式。
相比于变式1, 变式2的变量更加复杂在数列的构建中, 更加要求变量元素的有效分配, 实现通项式求算。
变式3:数列{an}中, a1=1, 且an+1=2an+3n+1, 求{an}通项式。
变式3所加上的变量变式为3n+1, 更加复杂, 且为3的幂次方, 这样的情况之下, 数列的构造就更难, 要求学生能够在原题及变式1、2的基础之上, 进行基础知识及经验的总结, 对于类似题目能够快速的、有技巧的解决。
注:该例题的变形, 在于由加上常数到加上变量, 再到幂的N次方, 由简入难的变式演绎, 能够更好地强化对基础知识的理解及应用, 并在知识的拓展中, 提高学生运用知识的技巧, 能够对系列相关问题的有效解决。变式1、2、3均是常见的考试题型, 是对等比数列知识的重点考查方式。
数学复习在于“固本”, 能够从基础知识出发, 通过一题多变的思想, 构建开放式的学习空间。对于高中生而言, 要在日常的复习学习中, 培养良好的学习习惯, 并习得复习技巧, 在扎实的“基础”知识之上, 更好地从“变”中获得知识的深度和广度, 这才是有效的数学复习。因此, 在数学复习中, 要善于从简入繁, 从繁重获得知识的规律, 更好地掌握知识要点, 提高数学复习的科学性, 形成数学核心素养。
3、 从“变”中学会贯通, 有效拓展知识学习面
融会贯通的复习技巧, 是高中阶段数学有效学习的重要基础。在一题多变的思想中, 强调从“变”中学会贯通, 能够从一般结论, 开展多种变式题的有效学习, 能够进一步提高复习质量。在复习中发现, 一些学生对基础知识的应用“滚瓜烂熟”, 但对于“变式”中的知识应用, 则表现出较大的不适应性, 这很大原因是缺乏学会贯通, 思维不活跃, 对于知识面的深入探究比较欠缺, 以至于学得不够深、不够精。为此, 在复习过程中, 要善于从“变”中寻求规律、总结知识, 进而在举一反三的多变题中有效解决各类问题。
函数最值求算是高中数学知识的重要内容, 也是易“变”题型, 对学生的学习能力有较高要求。这就需要学生在复习中懂得知识的贯通, 抓住知识点, 懂得拓展性应用。
例:函数y=-x2+4x-2的最大值是多少?
对于复习阶段的学习, 该题目十分简单, 强调学生能够对二次函数性质、单调性等知识的有效掌握, 对于简单的最值问题能够快速解决, 这对于提高复习效率, 巩固知识点非常重要。
变式1:函数y=-x2+4x-2在区间[0, 3]的最值分别是多少?
相比于原题, 变式1设定了最值求算区间, 这就要求学生在复习中, 能够基于轴定区间, 通过二次函数的性质, 快速求算出最值。对于知识学习不牢靠的同学而言, 给定区间下的求算, 相对比较难, 对知识的理解及应用要求更高。
变式2:函数f (x) =-x2+4x-2定义区间[t, t+1]上, 求函数最值。
对于确定的二次函数, 其定义区间却随参数的变化而变化, 这种题型更加复杂, 但万变不离其宗的是, 要求学生能够掌握定义区间、二次函数性质等知识, 能够在融会贯通中, 以不变应万变, 实现对最值的有效计算。
变式3:已知x2≤1, 且a-2≥1, 求函数f (x) =x2+ax+3的最值。
函数不确定, 要求学生基于已知条件, 运用函数性质, 通过对变量a的控制, 在固定的定义区间, 求算出函数的最值。该变式转换了原题及变式1、2的知识模式, 让学生能够在复习中懂得如何转变思维模式, 能够基于内化的知识, 去寻找不同题型下知识的多样化变式, 提高复习效果。
注:函数最值求算可简亦可难, 关键在于对知识的融会贯通, 懂得从不变中发现变的规律, 掌握该类题型下知识的综合应用。复习是学习的巩固阶段, 同时也是融会贯通的环节, 需要有效拓展知识学习面, 掌握知识的精髓。
数学知识的系统性, 要求知识复习的关键, 在于掌握好知识要点, 能够在不同题型的构建之下, 确保有效复习的开展。易简之题可拓展, 拓展之题可寻规律, 在开放式的思维视角之中, 强化对知识内在联系的认识, 能够从一题多变的复习空间, 促进知识的深入理解, 转变对知识的认识。
4、 从“变”中强化应用, 促进发散性思维生成
实践应用是复习的重要环节, 更是深入理解的重要保障。在高中数学复习中, 从“变”中落实应用, 以更好的促进发散性思维的生成, 这是复习技巧的重要落脚点。特别是随着高考改革的不断推进, 在高二年级的复习中, 知识的系统性更加强调应用环节的突出, 能够对知识的系统构建, 进而提高复习质量。笔者在数学复习中, 注重难点知识的逐一击破, 在多元化的思维空间, 促进知识应用的完备性。
立体几何是高中阶段的重要知识点, 知识的抽象性更加要求复习的开展, 应基于定理性质应用训练, 实现对知识的有效掌握。在立体几何中, 线面垂直、线线垂直等性质定理, 是常见知识点, 也是证明应用的难点所在。为此, 在对立体几何的知识复习中, 更加强调知识应用的导向性, 通过应用训练, 拓展知识面, 提高数学复习的有效性。
例:如图所示, 四棱锥P-ABCD中, AB∥CD, 且∠BAP=∠CDP=90°。证明:平面APD⊥平面PAB。
该题在问题的设置中, 更加注重基础性质定理的应用, 强调对知识的巩固性认识。
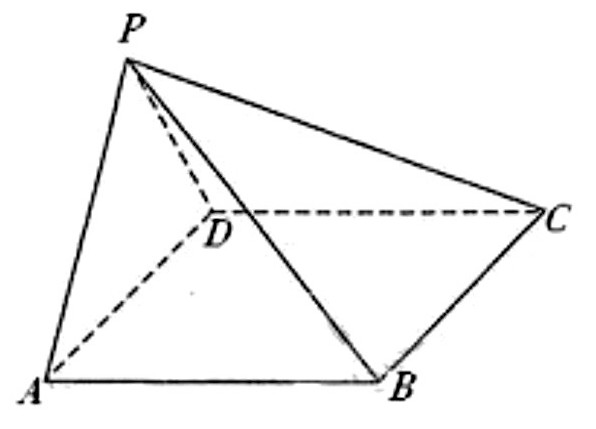
但在变式中, 可从设问出发, 对设问难度进一步加强, 强化学生对知识的应用, 通过也拓展对知识的理解。
变式1:若PA=PD=DC, ∠APD=90°, 且四棱锥P-ABCD的体积为8/3, 求四棱锥P-ABCD的侧面积。
变式1的设问, 对于文科生而言, 比较适中, 但对于理科生而言相对比较简单。在原问的基础之上, 通过设问条件的加强, 让复习的着力点更加突出知识的完备性, 能够从实际出发, 立足学习所需, 让复习效果更加显着。
变式2:若PA=PD=DC, ∠APD=90°, 求二面角A-PB-C的余弦值。
问题的“变”, 更加要求不仅需要对基本性质定理的学习, 而且需要懂得二面角的求算, 这是提高知识应用能力的重要途径。针对学生对知识的掌握程度, 设问的变式更加强调知识的综合应用, 能够从立体感的培养中, 更好地应用知识, 获得良好的学习效果。
复习是应用的基础, 也是强化对知识构建的重要过程。对于知识的应用训练, 能够从不同的思维视角, 提高对知识的理解与认识, 能够更好地把握知识点, 促进有效学习的实现。作为高中生, 应善于在“一题多变”的实现之中, 获得对知识的不同理解与认识, 懂得从不同的思维切入点, 实现对知识的系统构建, 以更好地提高复习效率与质量。
5、 结语
综上所述, 高中生处于个性发展的特殊阶段, 有效复习的构建, 在于如何依托有效的复习方法、科学的复习安排, 在一题多变的思想中, 提高复习的效率与质量。在本文的探讨中, 高中生在数学复习中, 要从一变应万变的思维切入点, 强化对知识的归纳、汇总, 并在“变”中拓展知识点。立足学习经验, 高中数学复习的开展, 关键在于夯实三个复习面:一是要从“变”中扎实基础, 促进知识深入理解;二是从“变”中学会贯通, 有效拓展知识学习面;三是从“变”中强化应用, 促进发散性思维生成。
参考文献:
[1]乐文栩.浅谈“一题多变”在初中数学课中的应用[J].当代教育实践与教学研究, 2016 (2) .
[2]王亮.浅析“一题多变”在高中数学教学中的应用[J].教育, 2015 (12) .
[3]朱庆云.一题多变天地宽——浅谈初中数学的解题与析题[J].数学学习与研究, 2017 (8) .
[4]高山林.一题多解和一题多变在高中数学教学中的应用问题探讨[J].高考, 2014 (5) .
[5]陈亚伟.巧用一题多变培养学生数学思维能力[J].数学学习与研究, 2015 (7) .





