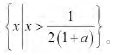
例 3 已知目标函数 z=2x+y,且变量满足下列条件:
x-4y燮-33x+5y<25,x叟叟1求 z 的最大值。
解:根据题意画出满足不等式的图像,如图所示:
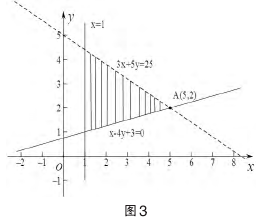
得在直线 x-4y=-3 与直线 3x+5y=25 的交点 A(5,2),当目标函数z 过交点 A(5,2)时有最大值,zmax=2×5+2=12.
2.4 解决圆锥曲线的问题
例 4 某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观察点同时听到一声巨响,正东观测点听到巨响的时间比其他他两个观测点晚,已知各观测点到中心的距离都是,试确定该巨响的位置(假定当时声音传播的速度为,各相关点均在同一个平面上)。
解:以接报中心为原点 O,正东、正北方向为 x 轴、y 轴正向,建立直角坐标系, 设 A、B、C 分别为西、 东、 北观测点, 则 A(-1020,0),B(1020,0),C(0,1020),通过建立坐标系,结合双曲线的定义则可解决。

设 P(x,y)为巨响发生点由 A、C 同时听到巨响声,得 PA = PC ,故 P 在 AC 的垂直平分线 PO 上,PO 的方程为 y=-x, 因 B 点比 A 点晚4s 听到爆炸声,故:PB - PA =340×4=1360.由双曲线定义知,P 点在以 A、B 为焦点的双曲线x2a2-y2b2=1 上。
依题意得:a=680,c=1020,所以:b2=c2-a2=10202-6802=5×3402,故双曲线方程为:x26802-y25×3402=1,用 y=-x 代入上式,得:x=±680 姨 5.因为PB > PA ,所以:x=-680 姨 5,y=680 姨 5,即 P(-680 5姨 ,680 姨 5),故 PO =680 10姨 .
3结语
总之,数和形是不可分割的两个有机整体,相辅相成的,数从量的关系上反映问题,形从直观上反映问题。 数形结合,取长补短,优势互补往往能有效的解决问题,用处很大,可能衍生许多的解题技巧。
【参考文献】
[1]姜建平.浅析数形结合思想在解析几何中的运用[J].理科考试研究(数学版),2012,12:25-26.
[2]谢伟文.数形结合思想在函数中的应用[J].解题策略,2012,12:88-89.
[3]何新艺.数形结合在极值与最大值问题中的应用[J].中国校外教育 ,2010,12:129-130.
[4]张宝贵.一类圆锥曲线最值 问题的通解探究 .2012,(200240)[J].珠 江教育论坛,2012,3(1):49-50
[5]王景超.数形结合思想在解题中的应用[J].名师专题讲座,2006(3):18-20.
[6]肖军委.高中数学中数形结合思想的应用研究[J].中 国新技术新产品 ,2010(15):234.
[7]郑米云.优化数形结合 提高解题能力[J].新课程研究,2012(3):181-183.





