初三数学第一轮复习中的结构性复习策略

九年级数学教学论文第四篇：初三数学第一轮复习中的结构性复习策略

 

　　摘要：通过对近几年上海市中考数学试卷的分析,不难发现上海市中考数学试卷命题注重对“四基”考查的同时重视对数学知识的真正理解和学以致用,关注学科能力素养,注重实际应用能力、文字阅读能力和探究性学习能力.试题重视背景材料的选择和设计,并以适当的图表、图形、图像等不同的形式呈现,力求体现时代性和多样性,体现数学知识的应用价值.这就要求教师在复习课中更需要注重对数学本体知识内在联系的思考,因此,笔者认为,在中考数学第一轮的基础知识复习时,更需要注重知识结构体系和知识之间的关联.

 

　　关键词：复习课; 初中数学; 知识结构; 知识关联;

 

　　面对初三的复习,尤其是第一轮复习知识点的梳理阶段,很多学生思想上不够重视,总觉得都学过,没有必要把时间浪费在基础知识上,应该多练习综合题.同时现在部分复习课也存在很多问题,主要表现在:复习课变成了练习课,甚至搞题海战;教师替代学生做整理,学生成了记录员或听众;停留在知识梳理和练习巩固上,缺少提升性指导.为了改进这种不足,结合笔者的教学实践,从知识结构和知识关联两个方面提出以下的策略.

 

　　一、以结构的方式复习知识点,注重知识的整体性

 

　　(一)知识的框架性结构清晰化、提炼知识“由厚到薄”的过程

 

　　由于学生不同年龄段的理解能力和认知能力不同,许多有关联的数学知识点是分散在各年级、各章节中的,新授课中也是一部分一部分的进行学习,所以在第一轮复习时,应有意识地研究如何从培养学生的系统化思维的角度出发,引导学生对知识进行系统的整合,有意识地让学生构建知识“框架”,让学生把学到的零散知识整合起来,清晰前续知识与后续知识之间的逻辑关系,引导学生对知识点进行系统梳理和沟通联系,把知识构建成一个牢固的“框架”,在学生脑海中有效构建数学知识体系.

 

　　例如,在复习三角形时,可采用按照图形的大小和形状两个方面建立框架,进行复习,图形的大小相等、形状相同就是学生熟悉的全等三角形,图形的大小不等、形状相同就是学生比较怕的相似三角形,图形的大小相等,形状不同是学生学过的面积相等的三角形,图形的大小不等、形状不同就是比较一般的三角形,因没有特殊性,也就不在我们研究的范围内,但作为一种情况要列出来.再如,函数系列就有其框架性结构,所学过的正比例函数、反比例函数、一次函数、二次函数,都按照概念、图像、性质这个结构学习的.所以在复习时也按照概念、图像、性质这一框架结构复习.可采用知识结构图或表格的形式整理出来,进一步体会函数的框架性结构.

 

　　教师从整体的角度来进行教学设计,不仅能达到复习知识的目的,还能引发学生思考,进而整合所学的概念和知识,形成一个知识框架网,此时再以习题辅助的方式进行复习会更科学和更合理.

 

　　(二)学习过程的方法性结构、加深对知识纵向联系的深度认识

 

　　数学注重举一反三、注重循序渐进、注重环环相扣,由于数学本身存在的这些特点,所以在复习中,我们要把数学知识的种类、结构、定理仔细研究,就会发现知识之间都是有必然的联系的,有的由浅至深,有的似曾相识,有的相辅相成,复习时可以把类似的知识、方法进行比较、联想,建立结构,使学生更清晰地认识知识点.

 

　　例如,在复习特殊图形(等腰三角形、平行四边形、矩形、菱形、正方形、等腰梯形)的性质时,引导学生从边、角、特殊的线段和图形的本身即对称性,从这四个角度去思考特殊图形的性质,等腰三角形是所学特殊图形的方法性结构的基础,教学是一个教结构的过程,而平行四边形是特殊的平行四边形这个系列的基础,也是用结构的过程,所以在复习特殊的图形时,可通过表格的形式从边、角、特殊的线段和图形的本身即对称性,这四个方面回忆性质.可通过表格的形式展示出来,进一步体会知识之间的结构.

 

　　从知识的方法性结构体系来切入,建立结构、教结构、用结构来进行初中数学中的复习.通过特殊图形之间的方法性结构的复习,学生对知识的理解不会只停留在表面,会在头脑中构建自己的知识网络,同时还帮助学生逐步扩大知识复习的视野与范围.

 

　　二、以类比的方式复习知识点,注重知识的关联性

 

　　(一)沟通知识的内在关联、体会知识“由薄到厚”的过程

 

　　初中数学教材中有很多有联系的知识点,教师可以利用这些知识点之间的相关性,在复习时组织学生观察、思考,进而指导学生通过分析得出结论,可以让学生对所学的知识能更好地归纳、总结,更有利于学生掌握知识之间的关联性.因此,初三第一轮复习时,把某些有关联的知识整合起来.这样在复习的时候可以通过联想、迁移、梳理、归纳等方法,把所学的知识统筹起来.强化关联知识内容间的逻辑关系,弄清楚不同知识间的内在或外在逻辑联系.

 

　　例如,一次函数与一元一次方程、一元一次不等式的关联,以下是复习课部分教学设计:

 

　　教师活动:

 

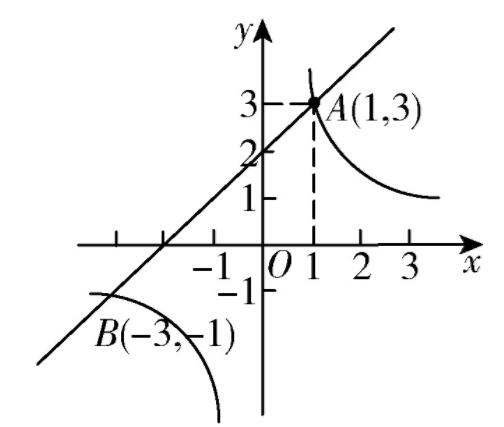
　　例1 如图1所示,求直线y=x+2与x轴的交点坐标.

 

　

 

　　图1   

 

　

 

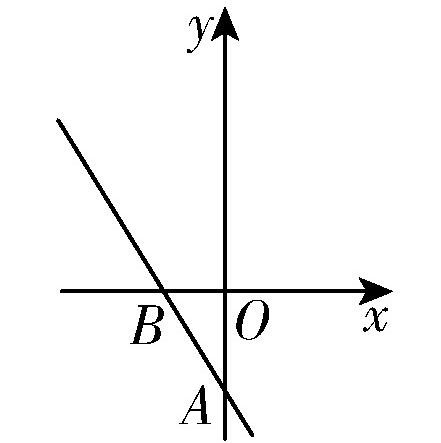
　　图2   

 

　　例2 如图2所示,直线y=kx+b经过点A(0,-2)和点B(-1,0),则关于x的不等式kx+b>0的解集为( ).

 

　　A.x<0 B.x<-1 C.x>0 D.x>-1

 

　　提问:一元一次方程及一元一次不等式与一次函数有什么联系?

 

　　学生活动:独立解答,并归纳一次函数与一元一次方程、一元一次不等式的联系.

 

　　设计意图:通过一次函数与一元一次方程、一元一次不等式的沟通,既为函数研究增添了活力,又为学生理解代数式以及解方程和不等式拓宽了思路,使学生在整体综合的意义上实现知识的融会贯通.

 

　　再如,二次函数与一元二次方程的关联,以下是复习课部分教学设计:

 

　

 

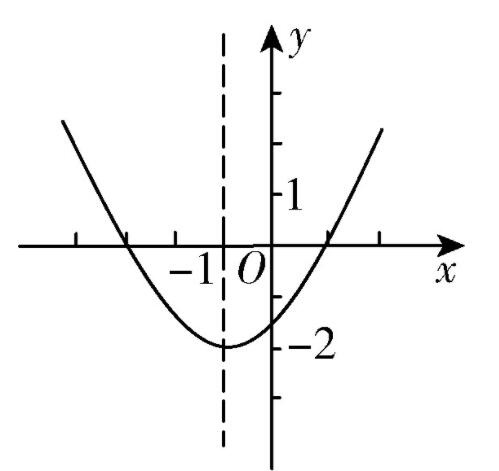
　　图3   

 

　　例3 指出二次函数y=12x2+x?32y=12x2+x-32图像的开口方向、对称轴和顶点坐标,并画出这个函数的简图.

 

　　(1)求抛物线y=12x2+x?32y=12x2+x-32与x轴的交点坐标.

 

　　(2)根据图像写出一元二次不等式12x2+x?32<012x2+x-32<0的解集.

 

　　提问:一元二次方程及一元二次不等式与二次函数有什么联系?

 

　　学生活动:独立解答,类比归纳二次函数与一元二次方程、一元二次不等式的联系.

 

　　设计意图:通过类比,归纳二次函数与一元二次方程、一元二次不等式的联系,

 

　　有利于提升学生主动学习的能力和习惯,并为学生的后续学习提供铺垫.

 

　　引导学生回忆所学的相关联知识,再统一呈现,引发学生的认知冲突,从而得到复习、巩固、提高的效果,这样可以帮助学生在头脑中初步建立知识之间的逻辑联系,为激发兴趣、建立知识结构打下较好的基础.

 

　　(二)沟通方法的内在关联、加深知识横向联系的广度认识

 

　　数学知识中有些知识之间存在某些方面的相似或相同,两者之间是存在着一定的联系的,有效地将两者联系起来,可以提高学生对数学知识的理解,也可以促进学生树立数学知识的应用意识,提高学生数学知识的综合应用能力.所以在第一轮复习时要理清两个对象研究方法之间的关联,通过这种方法之间的关联,加强对所学知识的对比,体会知识间的关联,在头脑中构建清晰的知识结构,形成知识网络.

 

　　例如,在复习三角形时,从一般三角形到特殊三角形之间就有着方法之间的内在关联,从概念出发当边特殊化时就变成了等腰三角形,当角特殊化时就变成了直角三角形,当边和角同时特殊化时就变成了等腰直角三角形,通过边和角的特殊化,各自的性质也就凸现出来了.以下是复习三角形时的部分教学设计:

 

　　问题1:三角形的边有什么关系?三角形的角有什么关系?

 

　　问题2:三角形可怎么样进行分类?

 

　　问题3:画一个任意的三角形,并画出三角形的所有中线、高线、角平分线.

 

　　问题4:等腰三角形是三角形边特殊化得到的,那么等腰三角形的边和角有什么特点?

 

　　问题5:画出一个等腰三角形,并画出底边和一腰上的中线、高线、和它对角的平分线,你有什么发现?

 

　　问题6:直角三角形是三角形的角特殊化得到的,那么直角三角形的边和角有什么特点?

 

　　问题7:直角三角形的斜边中线有什么特点?

 

　　问题8:当直角三角形中有一个锐角等于30°时,直角三角形的边又会有什么特点?

 

　　问题9:等腰直角三角形是三角形的边和角同时特殊化得到的,它的边和角有什么特点?

 

　　再如,在复习一般四边形到特殊四边形时,当边的位置关系发生变化时,就得到了两类特殊的图形,两组对边分别平行时是平行四边形,一组对边平行而另一组对边不平行时就是梯形.特殊的平行四边形和特殊的梯形就可通过与平行四边形和梯形之间存在的方法间的关联进行复习,达到巩固提高的目的,也进一步体会到知识之间的关联.以下是复习特殊四边形性质的部分教学设计:

 

　　问题1:矩形是怎么定义的?

 

　　问题2:矩形是平行四边形角特殊化得到的,在角度变化过程中平行四边形中的各元素和图形本身发生了什么变化?

 

　　问题3:通过上述的变化可以得到哪些矩形有别于平行四边形的特殊性质?

 

　　问题4:菱形、正方形是怎么定义的?

 

　　问题5:菱形、正方形是平行四边形的哪些元素特殊化得到的,在变化过程中平行四边形中的各元素和图形本身分别发生了什么变化?

 

　　问题6:通过上述的变化可以得到哪些菱形、正方形有别于平行四边形的特殊性质?

 

　　问题7:正方形可通过矩形、菱形中哪些元素特殊化得到,在变化过程中矩形、菱形中的各元素和图形本身分别发生了什么变化?

 

　　借助于这样层层递进的复习过程,可以帮助学生形成数学知识复习的整体性并掌握数学知识之间的内在联系.以相关单元知识为起点,对单元知识之间内在联系的沟通与整合,从横向角度对相关单元知识进行结构组块.

 

　　在“初三数学第一轮复习课教学设计的实践研究”的探索与实践中,笔者欣喜地发现,多角度的复习,更能吸引学生的注意力,对原本感觉零散、杂乱的知识整合出方向,极大地调动了学生学习的积极性和主动性;学生在复习阶段对数学知识的结构性更清晰明了,没有“题海”训练的包袱,也一样取得理想的成绩,学生数学学习的精神面貌也得以改善.同时教师在贯彻、推进二期课改理念的同时,教学方法与手段逐步得到提高,初步收获到了教学研究的乐趣和信心,这给笔者的探索之路带来了很大的动力,在今后的教学过程中,笔者会朝着研究型教师的方向不懈努力,继续发现,不断进取!

 

　　参考文献

 

　　[1]吴亚萍.“新基础教育”数学教学改革指导纲要[J].桂林:广西师范大学出版社,2009.

　　[2]叶澜.重建课堂教学过程观——“新基础教育”课堂教学改革的理论与实践探究之二[J].教育研究,2002(10):24-30,50.