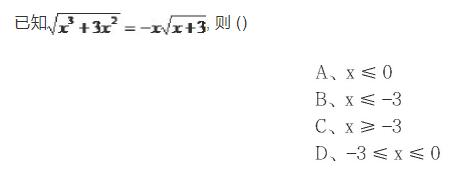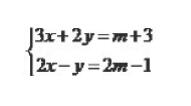摘要:近几年“大数据”“数据分析”名词常常进入我们的视野, 说明了这类事件或工作已经在我们的生活中越来越多的存在, 越来越起着重要的影响。而“数据分析”人才应该具有怎样的能力?在我们初中阶段又可以怎么培养孩子们的这样面能力?我们在下面讨论一下。我们研究得出, 初中数学解题过程一边有四个环节:1、读清题目;2、分析题目;3、寻找解决方案;4、解决问题。往往我们在第1、3、4、环节中都花尽了心思, 而且往往立竿见影, 成绩一下子就上来, 见效很快。但是我们也发现, 到了初三的学习, 原来初一初二学习成绩比较好的同学后劲不足, 而且很明显他们应对“大题”“难题”时就找不到方法了。本人认为很可能是一直以来, 孩子们的教育缺乏了“分析能力”的培养。“分析能力”是人在思维中把客观对象的整体, 分解为若干部分进行研究、认识的技能和本领。这样能力的培养, 应该在初一数学教学就开始培养, 从基础知识研究开始培养, 从较简单的综合问题开始培养。
关键词:分析能力; 解决问题的三个环节; 整体分解为部分;
现在的初中数学教学着眼于“读题”与“解题”, 很少把时间花在“分析问题”上, 这样的教学在初一、初二可以得到不错的效果, 但是到了初三, 原来成绩不错的孩子学习变得非常辛苦, 很多学习成绩不升反降。还有一种情况就是, 老师课堂上讲过的题目, 很多同学都能听明白了解题的方法, 但是考试时又遇到类似的题型, 我们的孩子又做不出来了, 考后我们老师再点评一下, 他又恍然大悟。究其原因, 就在于在“读题”与“解题”之间, 我们没有做好“分析问题”这一衔接工作, 它是把问题与解题方法联系起来的纽带。没有对问题进行透彻的分析, 就不能用好每个条件;找不到条件之间的关系;理不出问题的关键所在, 从而找不到解决问题的有效方法。相反, 假如我们能把孩子们的“分析题目”能力也提升上来, 那他们就能用好每个条件;找到条件之间的关系;理出问题的关键所在, 从而找到解决问题的有效方法。
一、分析能力的重要性
去年有幸参加区举办的一次北京学习活动, 期间到一所民办学校交流, 学校的介绍人有一段对名师的评价让我感触很深, 她是这样说的:教学好的老师, 不一定立刻初一、初二就出成绩, 可能她们带的班成绩一般, 但是到了初二、初三他所教的孩子后劲就来了, 就会反超其他班的孩子。虽然这位介绍人没有说其中的原理, 但这个问题引起了我的共鸣, 我心理好像也一直在存在类似的问题, 在寻找这方面的答案。回来之后我不断的在这个问题上思考、研究, 最后我得到的结论是:我们的教学很多时候缺少了“分析问题”这个环节, 没有打通问题与方法之间的通道。而孩子的分析能力不是一天两天的可以培养出来的, 它是一个孩子综合能力, 综合素养, 需要累积、沉淀。
我们知道:分析能力是对事物本质属性以及事物之间的内在联系的深刻揭示能力。事物的现象是纷繁复杂, 变化万千的, 要对这些现象进行加工整理, 从中找出内在的联系和规律, 就必须掌握一套科学的分析方法, 提高自己的分析能力。
所谓分析, 就是把事物的整体分解为部分, 把复杂事物现象分解为简单要素并加以研究的一种思维方法。分析离不开分解, 分析象一把解剖刀, 把事物的本质属性及事物之间的内在联系揭示出来, 成为人们决策的依据, 行动的向导。
所以学生做题的时候, 如果能把问题分析细致, 就能更容易找到解决方法。在教学中我们总在意做了多少题, 见过许许多多的解题方法, 但是学生如果没有很好的“分析题目”的能力, 就很难找到条件的内在联系, 很难找到解决问题的方向与关键所在。尤其在解决大题时, 分析问题, 把握问题关键显得尤为重要, 这往往是取得高分的关键。
二、如何培养学生的分析能力
既然题目的分析能力这么重要, 那我们该如何培养呢?下面谈一下我们的做法。
经过学者们的研究知道, 分析能力的提高是靠多种因素主导的, 可归类为: (1) 知识储备 (知识的多元化) , (2) 掌握基本的分析方法 (自我分析能力) , (3) 平时的交流讨论 (分析方法多元化) 。
具体初中数学教学中, 培养孩子们的“问题分析”能力呢我们归纳为三个方面: (1) 条件分析; (2) 多角度分析; (3) 多条件综合分析。这三个方面没有界限, 但是层层提升, 在每节的教学之中, 都应该灌输进去, 培养分析的习惯。
1、简单的条件分析 (概念应用)
简单的条件分析, 是问题分析之中最简单、最基础的分析能力, 可以理解为简单的概念应用。条件分析的好坏, 取决于需要孩子对基础知识、基础概念的理解程度。所以, 简单的条件分析其实也在考察教师教授基础知识、基础概念的深刻程度。从初一开始, 我们上的基础知识课、概念课尽量体现理解的过程, 务求学的透彻, 学的深入, 为以后的分析做好准备。
简单的条件分析是题目分析的基础, 在整个初中阶段, 乃至于整个教学阶段都是非常重要。下面举例说明:初一题目:不等式的解集是, 则的取值范围?
这道题是考察学生的不等式的概念, 通过对比解的前后不等号的变化, 得出a-3<0这个结论。但孩子们很多是理解不了的, 关键在于在学习不等式概念的时候, 我们只是对不等号两边进行数值的推理, 而没有推广到字母或式子的范畴。
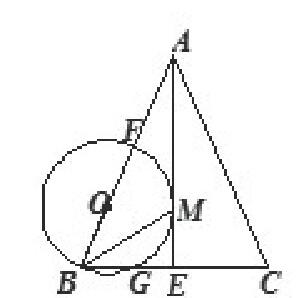
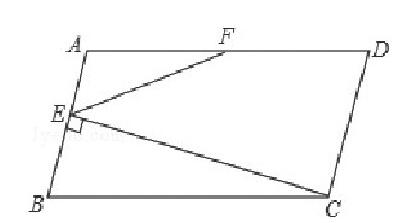
初三题目:如图, 在△ABC中, AB=AC, AE是BC边上的高线, BM平分∠ABC交AE于点M, 经过B, M两点的⊙O交BC于点G, 交AB于点F, FB为⊙O的直径.
(1) 求证:AM是⊙O的切线
(2) 当BE=3, cosC=时, 求⊙O的半径.
这道是考察学生基本概念的题目, 从条件可以分析出很多知识点, 如:BM平分∠ABC, 可以推出有可能要用到角相等的结论, 或者角平分线上一点到角两边距离相等的结论。而“ (1) 求证:AM是⊙O的切线。”应该明显分析为要连接OM, 然后证明AE⊥OM。通过这样分析, 我们就很容易得出 (1) 的解题思路, 是用“BM平分∠ABC”角相等的性质, 然后证明OM∥BE, 从而证明AE⊥OM。
2、问题的多角度分析
有时候一道题目可以有很多种分析方法, 而怎么分析, 做题更快更好呢?那我们平时就要训练学生的“问题的多角度分析”能力。问题的多角度分析能力, 就是培养学生的发散思维和综合能力, 帮助考生在许多的方法中找出正确的或更好的方法解题。很适合在平时课堂上让学生训练。几个例子如下:
初二题目:
这道题可以从两个角度分析, 可以从或去解决问题, 当然, 从不同的角度分析, 就有不同的解题方法。
初一题目:二元一次方程组
的解互为相反数, 求m的值.
这道题有两个不同的解题方法, 看我们怎么去分析。如果我们是看成是一个参数方程, 那我们先把x, y用m表示, 再利用后面“互为相反数”的条件求m。而如果先把“互为相反数”的条件列出一个关于x, y的二元一次方程, 那我们就可以有三个关于x, y, m的方程, 联立起来就可以求出m的值。
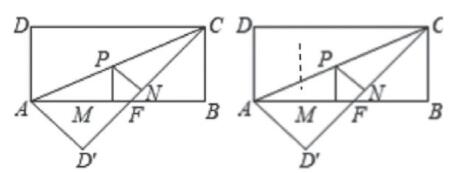
初二题:如图, 矩形ABCD中, AB=8, BC=4, 将△ADC沿AC折叠, 点D落在点D′处, CD′与AB交于点F.
(1) 求线段AF的长.
(2) 求△AFC的面积.
(3) 点P为线段AC (不含点A、C) 上任意一点, PM⊥AB于点M, PN⊥CD'于点N, 试求PM+PN的值.
分线的性质”或“等积法”两个方向解题。
3、条件之间的综合分析
简单说就是综合分析能力, 是更高层次的能力, 这个对解决大题至关重要。往往对单个条件的分析、运用基本找不到大题的解题思路。要对条件进行综合分析、理解才能看清题目的本质, 找到解题的方向。这里举几个例子如下:
中考题: (2012·广州) 如图, 在平行四边形ABCD中, AB=5, BC=10, F为AD的中点, CE⊥AB于E, 设∠ABC=α (60°≤α<90°) .
(1) 当α=60°时, 求CE的长;
(2) 当60°<α<90°时,
(1) 是否存在正整数k, 使得∠EFD=k∠AEF?若存在, 求出k的值;若不存在, 请说明理由.
(2) 连接CF, 当CE2﹣CF2取最大值时, 求tan∠DCF的值.
这道题的信息不多, 关键是我们要把条件联系起来。从条件“F为AD的中点, CE⊥AB”联系起来分析, 就有机会考虑到直角三角形的斜边的中线, 从而做辅助线:延长EF交CD的延长线构造直角三角形。但如果我们把“F为AD的中点”单独理解为AF=FD, “CE⊥AB”理解为∠ECD=∠BEC=90°, 从连接辅助线FC是得不到结果的。
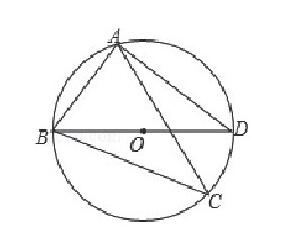
中考题:25. (14分) (2016·广州) 如图, 点C为△ABD的外接圆上的一动点 (点C不上, 且不与点B, D重合) , ∠ACB=∠ABD=45°
(1) 求证:BD是该外接圆的直径;
(2) 连结CD, 求证:AB=BC+CD;
(3) 若△ABC关于直线AB的对称图形为△ABM, 连接DM, 试探究DM2, AM2, BM2三者之间满足的等量关系, 并证明你的结论.
这道题目明显是要进行条件的综合分析。问题 (2) “连结CD, 求证:AC=BC+CD;”中如果与条件“∠ACB=∠ABD=45°”一起理解, 明显是构造一个等腰直角三角形, 而其中的“AC=BC+CD”条件, 可以猜到是截取或延长构造等腰三角形。而问题 (3) 就更容易找方向了, 综合已有的条件, 明显要构造一个直角三角形, 而且三边是分离的, 很可能要通过旋转的想法来构造直角三角形。当然, 分析方法还有许多, 这里不一一列举。而另一方面, 我们要知道学生的分析能力培养不是一两天的事, 它是一种能力, 一种素养, 那就需要一个过程, 要坚持去做。
三、结语
怎么去培养学生的分析能力, 是我们这几年教学的研究重点之一。我们从刚上初一就开始, 让学生们知道“分析问题”的重要性, 摆脱小学最求答案的习惯, 鼓励他们上课听好老师的分析过程, 对比不同的思路。从老师带着分析题目, 到学生自己分析题目, 我们慢慢的一步一步放手。虽然学生们初一、初二的成绩优势不明显, 但是他们到初三就可以学得更容易些。通过着手培养学生的分析能力, 在大题的得分方面, 这几年我们的得分率一直名列前茅。
参考文献
[1] 朱德全.现代教育理论[M].西南师范大学出版社, 2008, (2) .
[2]孙厚康.初中数学思想方法导引[M].浙江大学出版社, 2015, (6) .