摘 要: 教师着眼于学生认知发展水平与已有经验精心设计系列问题, 能令学生在生动活泼、主动而富有个性的学习中展开积极的思考, 积极探究、体验与运用数学思想方法, 并因此逐步积累起更加丰富的数学活动经验, 使学生在教师的有效指导中落实真正有意义的探究活动并获得学习的进步.
关键词: 初中数学,探究活动,基本形式
教师的启发诱导、学生的独立自主学习与合作讨论都是有效的数学探究活动必不可少的, 教师以问题为引领并启发学生在探究中发现问题、提出问题、分析问题与解决问题, 能令师生双方在共同探究的过程中获得富有个性化的思考, 学生这一学习的主体在数学探究活动中也会展现出更加丰富的思维动态与个性化想法.一般来说, 学生的探究活动可以分为独立探究、合作探究与引导探究这三种最基本的形式.
一、独立探究
独立探究这一探究活动中最基本的活动形式实际上就是学生个体对探究对象所进行的独立思考和探究.教师在一些较为基础或简单的数学知识的研究中, 可以设计一定的问题情境来引导学生独立思考和探究, 使学生能够在独立思考和探究中自主发现有关知识并完成一定的学习.
案例1:二元一次方程的建立.
教师在二元一次方程概念的建立过程中, 可以设计以下三个步骤引导学生独立探索.
(1) 创设问题情境.
长城这一中华民族伟大的象征西起嘉峪关, 东至辽东虎山, 全长约7300千米, 其中西段实际上是指嘉峪关到山海关这一路程, 东段则指山海关至辽东虎山这一路程, 西段比东段长约6100千米的距离, 那么长城的东段、西段的长度各是多少呢?
(2) 提出以下系列问题:
(1) 已知量和未知量分别有哪些?
(2) 有哪些等量关系?
(3) 可否列出一元一次方法来解决此题?
(4) 未知数有两个.假如设东段与西段分别长x千米、y千米, 用含有未知数x、y的代数式表示长城全长则为______;表示西段比东段长6100千米为______.
学生在解决第 (4) 问时往往易得以下两个方程:
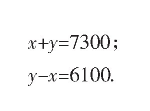
(3) 观察上述方程并归纳其特点.
学生往往能够表达出上述两个方程的部分特点, 教师可以在学生思考与归纳的基础上对其共同特点进行概括与表达, 直至将两个方程均含有两个未知数且未知数的次数都是1这一本质特点概括出来, 二元一次方程的定义至此也就顺利得出了.
学生思考并解决上述三个问题的过程正是二元一次方程建立的过程, 学生在亲身经历中对二元一次方程这一概念的产生形成了充分的认识, 学生在教师的精心设计中深刻体会到了源于生活而又服务于生活的数学及数学应用, 模型思想更易形成.
二、合作探究
以合作学习为前提所进行的合作探究是学习小组成员之间对研究对象进行的共同探究活动.一般来说.学生在合作探究之前必然已经进行过一定程度的独立探究, 合作探究往往是其独立探究后仍未能很好地解决时采取的一种探究方式.
案例2:多边形内角和.
教师在启发、指导学生合作探究多边形的内角和时可以设计以下三个步骤.
(1) 要求每个学生根据图1中的多边形进行独立思考并添加辅助线, 自主推导n边形的内角和公式.
(2) 组织学生将各自添加辅助线求n边形内角和的方法进行组内交流、相互比较并分享他人的成果.
(3) 引导全班学生进行合作与共同概括, 如图2所示, 添加辅助线的方法虽然多样且各不相同, 但分割多边形并将多边形内角和问题转化成三角形内角和问题是此处探究的实质.因此, 不管根据何种分割法进行计算, 最终得到的结果都是相同的.学生在独立探究、合作探究与全班探究、概括的整个过程中运用到了计算、归纳和发现, 最终在大家的共同合作与努力中获得了求n边形内角和的公式: (n-2) ·180°.
图1
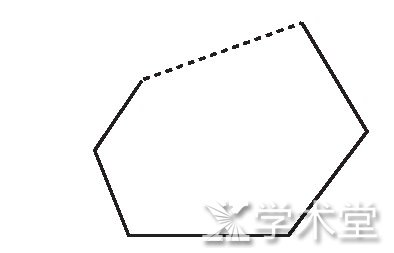
图2
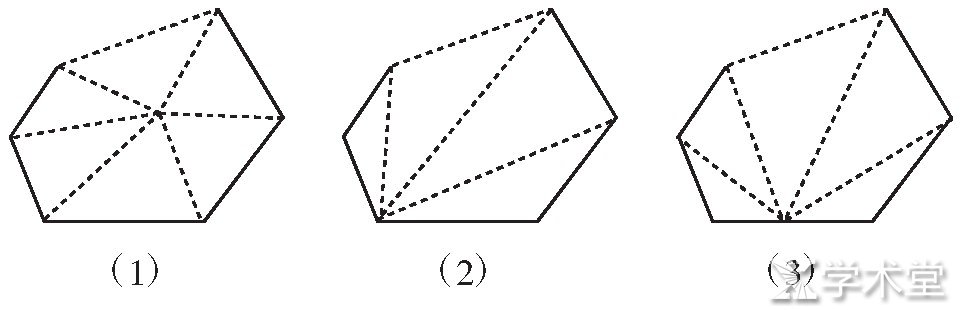
独立探究和合作探究在这一案例中都得到了体现.问题 (1) 的设计旨在引导学生进行独立探究, 使学生能够在独立思考中获得求n边形内角和的不同推导方法.问题 (2) 和 (3) 的设计旨在引导学生在独立探究的基础上进行合作探究, 使学生能够在合作探究中发现尽管分割方法不尽相同, 但殊途同归, 相同的结果都会在不同分割图形的方法中得到, 使得学生不禁产生是否具备共性的思考, 也因此引发学生的继续思考.
三、引导探究
教师引导学生对问题进行探究与思考即为这里所指的引导探究, 这种探究方式一般应用于学生独立探究和合作探究结束后又无结果或定论之时.教师在学生探究无力或束手无策之时引导学生探究, 往往能令学生获得灵感或继续探究的准确方向.
案例3:确定圆的条件.
不在同一直线上的三点确定一个圆这一内容往往不是学生独立探究与合作探究中能够轻易得出的, 因此, 教师在学生独立探究与合作探究的基础上, 可以采取引导探究的方式帮助学生获得知识.
(1) 在纸上作一点A并经过该点作圆, 大家能作多少个圆呢?
(2) 在纸上作A、B两点并经过这两点作圆, 大家能作多少个圆呢?圆心在哪里?
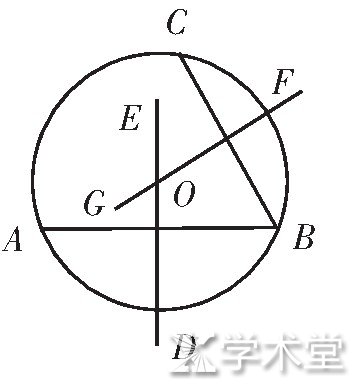
(3) 在纸上作A、B、C三点, 若A、B、C三点不在同一直线上, 经过A、B、C三点可以作出一个圆吗?若能, 应如何作出?圆心在哪里?经过A、B、C三点能作出多少个圆呢?
说明:学生在独立探索中即能解决问题 (1) 和 (2) :经过一个点能作出如图3所示的无数个圆;经过两点能够作出如图4所示的无数个圆, 所作出的圆的圆心都在如图4所示的虚线上, 已知两点构成的线段的垂直平分线即为这一直线, 这一重要的发现对于解决问题3来说极有价值.
不过, 学生面对问题 (3) 时往往颇感困难, 教师可以设计以下问题促成引导探究:
师:若经过A、B、C三点的圆O已经作出, 那么圆心O至A、B、C三点的距离如何?
生:相等.
师:到A、B两点的距离相等的点在何处?
生:在线段AB的垂直平分线上.
师:到B、C两点的距离相等的点在何处?
生:在线段BC的垂直平分线上.
师:经过A、B、C三点的圆的圆心应如何确定呢?
生:先后分别作出线段AB、BC的垂直平分线, 两线的交点即为圆心.
……
学生在教师的引导下很快作出了如图5所示的经过A、B、C三点的圆, 不仅如此, 还对该圆唯一作出了揭示.
图3
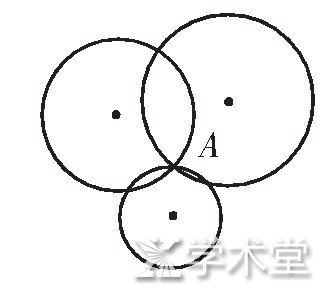
图4
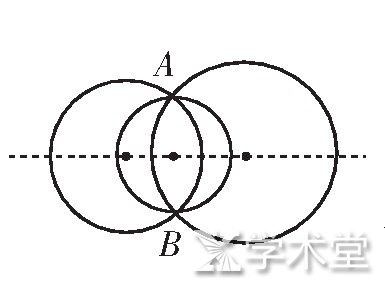
图5
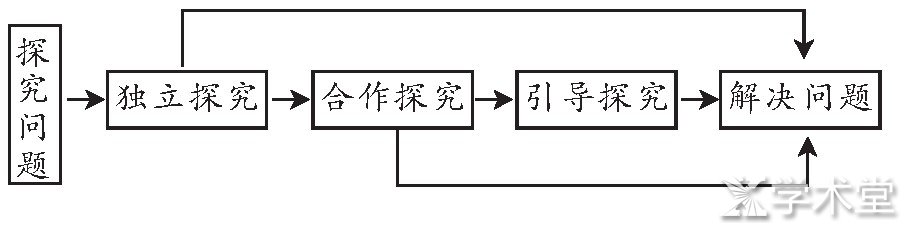
探究内容难易上的差异、学生探究能力的高低往往会决定探究方式的选择, 教师在具体内容的探究中, 不管选何种方式, 都应始终记住数学教育应令人人都获得良好发展的教育宗旨与理念.因此, 教师在具体教学中, 一定要遵循学生能够独立探究时就不采用合作探究的原则, 学生能够合作探究解决的问题也尽量不采用引导探究, 应使学生能够在独立探究的基础上获得最周全、细致的思考, 在必要的时候运用合作探究和引导探究作为补充.数学探究活动一般遵循如图6所示的具体过程:
图6
荷兰数学教育家弗赖登塔尔曾经对数学学习的方法表达过自己的见解, 强调实行“再创造”才是数学学习唯一的正确方法.因此, 教师在平时的教学中要坚持由学生本人去发现或创造, 杜绝将现成知识灌输给学生的简单做法, 运用情境设计、问题引领等多种手段与方法启发、引导、帮助学生实现这种再创造.





