一、研究背景
一、研究背景
态度是个人对某一特定对象所持有的评价总和与内在的反应倾向。[1]数学态度则是指向于数学的态度,包括对数学认知、情感和行为倾向三种成分。[2]继《全日制义务教育数学课程标准(实验稿)》[3]把情感态度列为一个数学课程目标之后,《全日制义务教育数学课程标准(2011年版)》[4]再次把它作为一个方面的课程目标,并在前言部分、课程目标部分和实施建议部分都作了相关描述。可见,新旧义教课标都非常重视学生在情感态度上面的发展。数学态度作为情感态度的一个重要方面,它对学生的数学成绩具有重要影响。积极的数学学习态度,使学生有一种专注于数学学习的倾向,并促进学生各项思维品质的发展,最终使学生在学习中获得成功。已有研究指出,学生的数学学习态度对学生的数学学习动机、行为、策略以及成绩产生很大的影响。[5]
目前,已有一些研究者对我国中小学生数学态度进行了调查[6-7],但是还没有专门针对初三年级学生数学态度的调查研究。初三学生在升学压力之下,思想、心理和行为等方面都具有一定的特殊性,更容易体验到心理冲突和挫折。数学态度一旦形成,就具有相对稳定性和持续性,而初三年级正是学生数学态度养成的关键时期。初三学生他们的数学态度如何,这还有待探究。鉴于此,本研究将对初三学生数学态度现状进行调查分析,以此来探究初三学生数学态度是积极还是消极;男女生之间是否具有显着差异;数学态度与数学成绩是否相关等问题。
二、研究设计
(一)研究工具
在调查研究中,测量工具的质量直接关系到研究结果的可靠性和可信性,它显得极其重要。目前国内外相关研究中测量数学态度最常用的是量表测量法。国外常用的数学态度量表有Sandman量表以及Fennema-Sherman量表等。其中最有影响的是Fennema-Sherman数学态度量表[8].本文采用国内学者何小亚等编制的《初中生数学态度量表》(MASHL)[9],该量表由学科态度量表与学习态度量表两个分量表构成,其中学科态度分量表有25个项目,分为有用性、愉悦性和倾向性共3个维度;学习态度分量表有27个项目,分为学习动机、学习信念和学习策略3个维度,量表信度较高、1MASHL为Likert式量表,采用5点记分法,部分题目是反向记分。正向题按照选项“完全不符合”“不符合”“不确定”“符合”“完全符合”依次赋值为1、2、3、4、5分,反向题反之。被试在每个维度上的得分取每个问项得分的平均值。
(二)研究对象
本研究对象选自黑龙江省佳木斯市一所普通中学初三年级的在校学生,共229名。此次共发放问卷229份,收回问卷216份,回收率94.3%;其中有效问卷203份,有效率为94.0%.在有效样本中,男生有100名,女生有103名。
三、研究结果
(一)总体分析
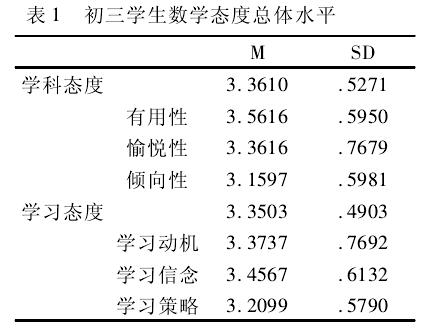
学科态度与学习态度结果分析:调查结果表明,初三学生数学态度发展总体处于中等水平,数学学科态度与数学学习态度两者差距较小,分别为3.36和3.35.
学科态度是指个体将数学看作一门学科知识时所持有的观点。由表1可知,有用性、愉悦性、倾向性这三个维度的得分相对平衡,得分均在“3”以上。其中有用性分数最高,为3.56,处于“符合”的量点上。愉悦性得分最低,为3.16.说明,初三学生更为认同数学的有用性,喜爱数学学科的倾向性较为模糊,这可能与生活、学习中对于运用数学,阅读数学的习惯有关。学习态度是指个体在学习数学过程中所获得的心理体验。由表1可知,初三学生学习信念得分最高,为3.46,学习策略得分最低为3.21.说明在学习态度方面,初三学生的学习信念较好,但学习策略的选择能力不强,疏于对学习内容的计划和安排。
(二)差异分析
1.学科态度、学习态度、数学态度的性别差异分析
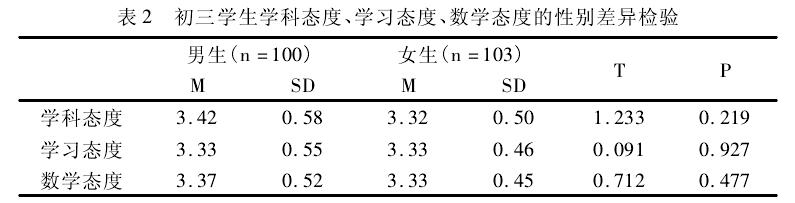
从表2可以看出,男生的数学态度和学科态度的平均分都略高于女生,但差距不明显,学习态度的平均分与女生持平。独立样本t检验中,两个群体的数学态度、学科态度、学习态度不存在显着差异(p=0.477>0.05;p=0.219>0.05;p=0.927>0.05)。
初三学生数学态度、学科态度、学习态度在性别上都不存在显着差异。随着数学课程改革的逐步推进,课堂上对于数学情感态度的的关注不断增加,尤其是基础教育阶段,越来越重视非智力因素在学习中的运用,因此不论男生还是女生,其数学态度都得到了较好发展。
2.数学态度与数学成绩相关性分析
3.不同成绩等级在数学态度上的差异分析
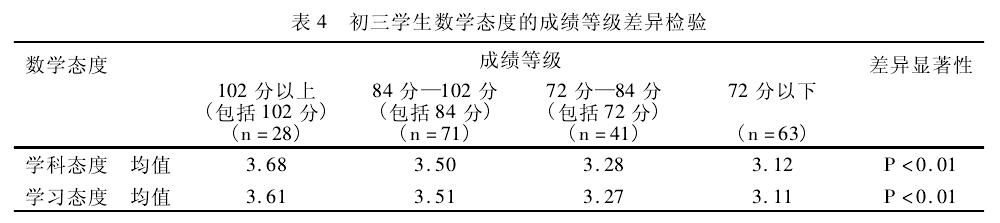
由表3、表4可知,数学态度与数学成绩呈现正相关,不同成绩水平初三学生数学态度具有显着性差异(P<0.01)。已有的实证数据也支撑了这些观点:国外有研究者对270名7年级学生进行了调查,结果显示数学态度与数学成绩显着相关。Degnan等人对初中学生进行的研究也得到了相似的结果。[10]国内的调查数据也表明,具有不同数学学习态度的学生的数学学业成绩有显着差异(F=18.50,P<0.01)。[11]
表4同时呈现了不同成绩水平初三学生在数学态度量表上的均分,数学成绩好的学生在数学态度得分相对较高,数学态度的得分随着成绩等级的提高也逐步升高。对此,研究者认为初三数学具有很强的复习性和综合性,初一、初二阶段整体的学习情况直接影响到初三阶段的学习。如果学生对于之前的学习内容掌握得稍差一点,初三阶段的学习就显得相对困难。长此以往,不愉快的情绪体验,使得成绩较差的学生容易获得消极的数学态度,对学习数学感到厌倦,因而不能努力学习导致较差的数学成绩,反之亦然。
四、讨论
在推进素质教育和创新教育的今天,培养学生的数学态度已成为教学的一个重要目标。调查表明:初三学生的数学态度总体处于中等水平;学科态度、学习态度在性别上均不存在显着差异;数学态度与数学成绩呈正相关;不同成绩水平初三学生数学态度具有显着性差异。基于调查研究结果,对以下问题进行讨论:
1.重视数学价值教育,关注学生情感体验的“亲历性”
传统教学活动中,相对于学生的情感体验,教师更为关注的是学生学业成绩,久而久之,大部分学生习惯于题海战术,形成了以记忆为主的学习方式。例如调查中,有51.2%的学生觉得“数学就是计算或证明”,“学习数学就是要反复地做题,之后记住它”,可见初三学生对于数学学习的过程的看法很模糊。长此以往,如果在学习中累积过多的失败经验,就极容易产生厌烦心理,形成不愉快的数学体验,导致消极的数学态度。基于此,教师要注意发挥自身的示范作用,有意识地给学生进行数学价值教育,摒弃以往旧课程中以运算技能操作、应试教育为价值取向,转而以注重过程、注重理解,培养学生的创新意识和实践能力为价值取向,多创设有意义的问题情境和活动。在数学学习过程中教师要重视学生数学学习的的“亲历性”,遵循学生数学学习的心理过程规律,注重学生的内心体验,不仅要学会数学知识、解决数学问题,更要点拨蕴涵于其中的思维过程和思想方法。
2.激发学生内部动机,培养数学学习的“审美性倾向”
调查中,初三学生在学科态度方面喜爱数学的倾向性不足,如仅有27.1%的学生喜欢看与数学有关的课外阅读材料,23.1%的学生喜欢用数学去解释日常生活中的一些现象,说明他们想要取得良好成绩的“功利性倾向”较为明显。这是数学态度总体发展水平不高的主要原因之一。但数学态度作为一种高级的、复杂的情感,具有相对稳定性,对于数学态度的培养在短期内不易有较大的提高。基于调查结果,转而培养和激发学生的学习动机可能会取得较好的效果,特别是内部动机。为此,一线教师应积极探寻能调动起学生态度和个人情绪的学习方式,使学生增加对数学学习的内在倾向。教师可以通过加强学生对数学学科本身优美性的感受和体验的方式,使学生对数学学习产生良好的内部动机,从数学学习的“功利性倾向”转向“审美性倾向”,进而使学习更具有自觉性和持久性,可以说学生能否具备这种动机是他们学习成败的关键因素。
3.关注数学态度与数学成绩的双向性,因材施教掌握评价技巧
数学态度是影响学生数学学习的非智力因素之一。在调查中,数学成绩与数学态度呈现正相关。数学态度可以通过学生自己数学学习活动的成败经验组织起来,在某种程度上说数学态度与数学成绩是相互促进的。已有的研究中也指出:数学态度与数学学习成绩是双向的。[12]基于这种双向性,教师要因材施教,帮助学生选择适合自己的学习策略,使他们对数学知识、数学学习过程以及对数学学习的把握程度有一个清晰正确的认识,在提高成绩的同时建立积极、健康的数学态度。在教学评价上,教师要掌握评价技巧,对学生的数学学习情感进行积极性评价,让学生相信自己有学习数学的能力,针对不同成绩的学生提出不同的要求,尤其是对于学业成绩较差的学生,多关注他们的情绪变化,尽量的多鼓励,少批评,给他们创设成功的机会,让每一个学生都能在成功中获得愉快的数学体验。
参考文献:
[1] 陶德清。学习态度的理论与研究( 第一版) [M].广东:广东人民出版社,2001:120.
[2] 姚静。关于数学态度学习的心理分析[J].数学教育学报,2001,10(3) :32 - 35.
[3] 中华人民共和国教育部制订。全日制义务教育数学课程标准( 实验稿) [S].北京: 北京师范大学出版社,2001.
[4] 中华人民共和国教育部。全日制义务教育数学课程标准(2011年) [M].北京: 北京师范大学出版社,2011.
[5]Schoenfeld A. Explorations of students'mathematical be-liefsandbehavior[J]. Journal for Researchin MathematicsEducation,1989,20(4) :338 - 355.
[6] 罗静,何小亚。重点中学高二文科学生数学学习态度调查研究[J].数学教育学报,2010,19(3)。
[7] 赵鹏程,杨伊生。小学生数学学习态度的调查研究[J].内蒙古师范大学学报: 教育科学版,2007,20(2) :102-104.
[8]Melancon J G,Thompson B,Becnel S. Measurement in-tegrity of scores from the Fennema - Sherman Mathemat-ics Attitudes Scales:The attitudes of public school teach-ers[J]. Educational and Psychological Measurement,1994,54(1) :187.
[9] 何小亚,李耀光。初中生数学态度量表的编制及信度效度检验[J].数学教育学报,2013,(3) :37 - 41.
[10]Aiken L R. Attitudes toward mathematics[J]. Review ofeducational research,1970:560.
[11] 李明振。成就动机、数学学习态度与学生数学学业成绩的关系[J].贵州师范大学学报: 自然科学版,1994,12(2) :48.
[12] 林泳海,陆冰花,刘登强。民族地区小学生数学学习态度调查研究[J].民族教育研究,2008,5(19) :33 -37.