摘要:在传统的教学中,数学教师在初三总复习时往往侧重于对复习卷的讲评,以及要求学生通过大量的习题,以达到巩固课堂的教学。这种教学方式能在某种程度上培养学生的解题能力,但耗时较多,学生困倦。本文主要以对初三几何总复习时,如何激发学生兴趣,开展有效的教学活动,在较短的时间内实现学生思维能力的有效培养和提升进行阐述。
关键词:初中数学;几何;思维能力
在初三总复习时,学生基础知识已经掌握。让学生在最短的时间内提升学生的解题能力,提升学生的思维能力,这与学生的学习效率以及学生对知识的融会贯通有极其大的关系。所以教师在教学活动中要注重学生的探究实践,应用有效的教学手段和方式,实现学生思维能力的灵活性,促进学生尽快养成良好的的思维习惯和思维能力。面对枯燥的复习课,教师利用探究的模式,激发学生的兴趣,能有效地提高学生学习的效率。具体做法如下:
一、精选例题,围绕本质问题设疑
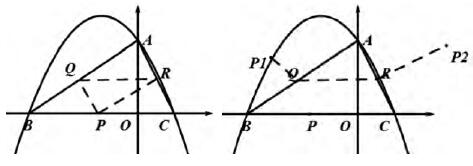
例:如图,在平面直角坐标系中,抛物线y = -2∕3x2 -4∕3x +2与x轴交于B,C两点(点B在点C的左侧),与y轴交于点A,若点Q是线段AB上的动点(点Q不与A,B重合),点R是线段AC上的动点(点R不与点A,C重合),求△PQR周长的最小值
问题①△PQR周长的最小就是哪些线段和的最小?
②过P作AB的对称点P1,则QP=QP1,同理过P作AC的对称点P2,则RP=RP2,这样QP +PR +QR =QP1 +P2R +QR,这样做,它的好处在于哪里?
∵Q,R都是动点
∴最小时应该P1,P2,Q,R共线时,从而转化为P1,P2之间的距离(两点之间线段最小)又∵P1,P2是动点,但它们都是随P的运动而运动。∴可设P(a,0),则P1(5a-24/13 ,12a +36/13)
P2(8-3a/5 , 4(1 -a/4)
∴P1 P2 =16/65√(65a2 +260)
∴当a=0时,P1P2的最小值为32√ 65/65.
③在解决过程中,涉及哪些最小值问题?
在传统教学理念的约束下,教师通常采用“单一性,强制性”的教学模式,讲一题算一题,使学生失去感知知识的魅力,压抑着学生探究知识联系的内在动力。所以精选例题,通过探究式的教学,围绕本质问题设疑能激发学生学习的积极性,体验知识联系的奥秘,能有效激发学生的思维,提升学生的思维能力。
二、挖掘本质,横向开放式设疑
以例题引入最值问题,建立最值的平台,让学生在最值这一平台中进行思考。在学生思考的过程中,类似于电脑的搜索功能,去搜索大脑中相关的信息。而且这种完全开放式的问题,给学生进行创造性学习提供了宽松、自由的环境,这样使得学生“主动思维”,“愿意思维”.在这种主动思考中,学生能得到三种与最值相关的知识点:1.垂线段最短;2.两点之间,线段最短;3.函数中的最值。所以线段和的最值问题通常可以通过对称直接用两点之间线段最短或者转化为某条线段的最值问题,或者转化为函数来解决。
三、建立模型,形成基本图形
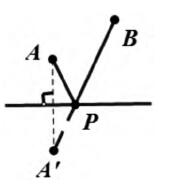
1.通过前面的讨论,通过对称直接用两点之间线段最短来解决最值问题的模型很快就可以建立(图1)
2.对于转化为某条线段的最值可以继续来设疑:即线段AB最小。线段AB要有最值,必定至少有一个是动点。∵若两个点都是定点,则线段固定,其长度一定是定值。那么动点可以怎么动?能不规则随意乱动吗?在这问题下,学生可以发现动点的轨迹一定是规则的轨迹图形,否则无法有它的最值,并且学生也能发现常见的点规则图形的轨迹为线和圆。从而引导学生总结出一动点,一定点和两动点问题,建立模型,得到基本图形。
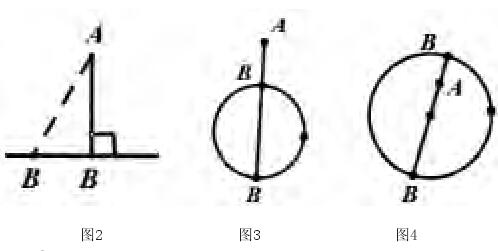
①点A是定点,点B是动点
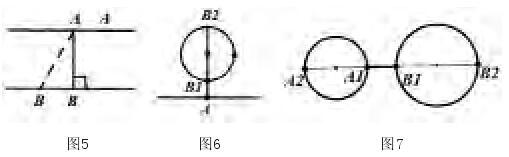
②点A是动点,点B是动点
③用函数来解决最值问题,这样把几何问题代数化。在初中阶段,如果给定自变量的区间,可以构造一次函数,二次函数模型,如果没有给定自变量的区间,一般构造二次函数模型。
学生构建基本图形的全部过程既是“数学化”的过程,又是思维训练,激发学生思维的过程,是让学生发现数学、“创造”数学、归纳数学的能力和提升数学素养的非常有效的途径。这需要教师引导学生通过分析、操作、猜测、尝试、解释、合作与交流等各项数学活动来实现,学生在这过程中要经历复杂而且有趣的数学思维过程,在这过程中,学生不仅可以构建几何的基本图形、获得了解决实际问题的思想和方法,同时,学生在主动思考中,感受到了学习数学的兴趣和学习数学的成就感,同时发展极大地提升了思维能力。
四、应用基本图形,解决相关问题
基本图形的应用价值取决于其它的广泛适用性,它能为复杂图形提供正确的的方向,找到解决问题的切入点。当然复杂图形可能多个基本图形的组合体,所以在应用时,不能盲目地套用。下面通过一例说明基本图形的应用。
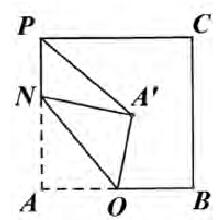
例:在边长为2的正方形ABCP中,O是AB边的中点,N是AP边上一动点,将△OAN沿ON所在的直线翻折得△‘OA N,连接PA'.求PA’的最小值。
分析:本题所涉及线段的最值,发现P为定点, 为动点。首先考虑 的轨迹是什么?因为 为定值,所以 的轨迹图形为一段弧,所以基本图形为图3,这样就能很容易发现其本质,寻找到突破口。
总结:以上的思维开放型的探究式的步骤为:
在这个过程中,能体现:1.整个教学过程充实,饱满,让学生体检数学的魅力。2.极大可能性地让学生参与到这推理过程,大大地增强了课堂教学的有效性,能很好地训练学生的思维,激发学生思维。3.在挖掘本质,建立基本图形的过程中不仅能培养学生的,数学思维,数学能力,还能潜移默化地帮助其构成知识间的联系,提高对知识的综合应用的能力。
参考文献:
[1]姜启源。数学模型[M].北京。高等教育出版社,2001.
[2]肖成全。有效教学[M].大连。辽宁师范大学出版社,2016(1)。
[3]魏彬。数学模型方法与小学数学教学[J].湖北教育,2000(18)。