
哲学和数学可以说是一对孪生兄弟,密不可分。在高等数学的教学过程中,有意利用哲学思想会让教学更灵活和富有新意。本文主要从哲学角度探讨高等数学的几个重要概念。
一、函数、极限、连续
(一)函数
现实生活中,每个人都有着错综复杂的关系。比如:朋友关系、师生关系、医患关系、父子关系等。对于两个有联系的事物在量上存在着的某种关系,数学中我们把它定义为函数,即 y=f(x)。
(二)极限
事物是发展变化的,但我们总希望在变化中发现它的稳定性,这在数学中就是极限。极限是微积分的工具,在其中占据很大的地位。不仅如此,极限在物理、工程等学科中有着广泛的应用,它揭示了变量与常量、无限与有限的对立统一关系。极限是个美好的东西,借助极限思想,人们可以从有限认识无限,从不变认识变化,从直线形状认识曲线形状,从量变认识质变,从近似认识准确。
我们每个人都在为了过上理想的生活努力奋斗。随着努力程度的增加,我们离美好事物也会越来越近。尽管如此,但有时还是触摸不到。这种想要而得不到的心情又加深了我们对美好事物的向往。极限思想恰好体现了我们追求美好事物的过程。例如对于一个数列1,12,13,……,1n,这里可以把n 增加 的 过 程视作 我们 努 力 的 过 程,把 极 限 值0视作我们的目标,显然随着 n 的逐渐增大,离目标0越来越近。极限是事物变化过程中呈现出的稳定性趋势。它与个别点的取值有关系,但个别点的取值又决定不了最终的趋势。比如我们经常听到的一句话“冬天来了,春天还会远吗?”冬去春来是大自然的内在规律,可能这个冬天有点暖,那个春天有点冷,但是,无论怎样都改不了四季轮回的整体趋势。
哲学中常说事物的发展是曲折上升的。这在极限中就可以体现出来。比如我们来看数列1-12,1+13,1-14,1+15,……,1+(-1)n 1n+1……,随着 n 的逐渐增大(这里我们可以将其看作某人逐渐努力的过程),这个数列的通项越来越接近极限值1(这里我们可以把极限1看作这个人奋斗的目标)。通过这个人的努力最终达到目标了,这解释了事物的发展是伴随着曲折和坎坷而不断上升的。可见在追逐美好事物的路途中虽充满了曲折和挑战,但只要认准了自己的正确目标,坚持到底,一定会达到胜利的彼岸。
(三)连续
哲学中事物的变化是从量变到质变。这在高等数学中也有明确的概念来对应。事物数量积累是连续的,量积累到一定程度变化到质,又是不连续的,也就是高等数学中谈到的间断点。经过质变之后,又进入了下一轮的量变过程,连续与间断如此反复促进事物的发展变化。当然对间断点稍做调整又可以实现连续,这也说明在一定条件下两者可以相互转化。
二、导数与微分
(一)导数
事物是变化的,这就决定了它们的关系也是变化的。当一种现象发生量的变化时,与之相关的另一现象也随之变化。数学中用增量表示变化。这里我们把吟x=x2-x1称为自变量的变化;吟y=y2-y1称为因变量的变化。 于是就有了研究变化与变化关系的概念即导数:
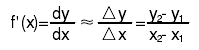
导数是讨论变化与变化的关系,这种变化关系有强有弱。根据变化的强弱可得到如下对应关系:(1)多变对多变;(2)多变对少变;(3)多变对不变;(4)少变对少变;(5)少变对多变;(6)少变对不变;(7)不变对万变。举例来说,对于(1)与(4),就一些奢侈品而言,如香水,它的价格变动时,人们的需求也会随之变化。若当其价格降为0时,需求最大。这就是弹性需求。对于(2)和(3),就如生活中的必需品,如馒头,即使价格降为0,人们对其需求也变化不大。人们对它的需求不因价格的变化而变化,我们称之为刚性需求。对于(5),就如在某人体温发生微小变化时,如上升了0.3度,对于这个人来说就会感觉到浑身不适。还有一个大家非常熟悉的“蝴蝶效应”---一只蝴蝶在巴西煽动翅膀会在得克萨斯引起龙卷风,说的也是小变化引起大变化的例子。对于(7),在高等数学中,常量与变量既有严格的区分,又相互依存、相互渗透,在一定条件下相互转化。再如,在多元函数微积分中,为了研究某一个变量的性态,往往把其余变量看作常量。
导数本质上体现了变化与变化的关系。然而要研究事物间的变化关系,必须弄清两件事:一是在什么范围内发生变化,也就是数学中所说的论域,只不过数学当中研究的是一种抽象的变化,脱离了具体的背景,如果我们把这种变化关系用到经济中就是边际与弹性问题。边际讨论的是绝对变化量的关系,弹性讨论的是相对变化量的关系。而经济学更关心的是边际效益。在经济学中有一个通用规律:边际效益递减。这一规律有着很广泛的应用。比如人与人的交往中,一开始大家都对彼此有很大的兴趣,但随着时间推移,我们会慢慢不在乎对方的一举一动,这正是平常所说的夫妻间的“七年之痒”.如果大家明白了这点,就会在自己今后的生活中学会创新。工作也一样,比如辅导员(父母)如果不厌其烦地重复一个模式、一句话,那么其发挥的功效就会慢慢减少。
(二)微分
世界的一切事物是相互联系的。导数是用极限来定义的,是关于函数变化率的问题;而微分是用函数变化率的线性主部来定义的,用于近似计算。两问题出发点虽然不同,但都揭示了同一问题的本质特征。
三、积分
事物之间的关系是对称也是相互的。比如在父子关系中我们可通过父亲找到他的儿子;也可通过儿子找到父亲。导数既然是讨论变化与变化的关系,那么按照关系的对称性,就理所当然地有导数的逆运算---积分。
积分学包含定积分和不定积分。单从概念上看,它们千差万别。不定积分是导数的逆运算,定积分是由研究面积、体积等问题发展起来的。后来,牛顿·莱布尼茨发现了它们的联系,也即着名的牛顿·莱布尼茨公式:

在此公式中,左边是定积分,右边是原函数在两个端点的差。不定积分与定积分共处于牛顿·莱布尼茨公式之中,互相依存,在一定条件下相互转化。一个小小公式中包含如此丰富的哲学道理,可见数学符号的美妙。
事实上,很多时候我们借助了微积分的思想。例如,国家的法律体系、医疗制度、教育公平、计划生育等都是具体而复杂的工程。国家来实施这些政策都是先对工程进行分解,即定积分的“分割”思想;每个阶段通常是先找到一个大框架,即定积分的“近似”思想;每个阶段都有近似解决方案,合起来就得到了整个工程的处理思路,即定积分的“求和”思想;最后是针对近似处理出现的小问题逐渐去接近大家期望的完美结果,即定积分的“极限”思想。
总之,哲学的思想在高等数学中有着广泛的体现。数学不仅是一门学科,还是一种思想方法。在课堂教学中融入哲学思维可以让学生体会到数学的辩证思维,在掌握高等数学的同时巧妙地与其他学科联系起来,实现全面发展。
参考文献:
[1]卢伟,程世娟。浅析高等数学学习中的辩证法思想[J].课程教育研究,2013(11):149.
[2]孟靖华。在高数中利用数学哲理性知识进行思维教学及人文教学[J].西昌学院学报,2013(2):143-145.
[3]姚秋妹,宋冬梅。高等数学中蕴含的哲学思想探究[J].产业与科技论坛,2014(17):94-95.
[4]尹波。高职数学中的哲学思想[J].山东行政学院学报,2012(6):143-144.
[5]赵昱。论微积分的哲学思想[J].作值工程,2014(10):327-328.





