摘 要: 以矩阵运算为例,探索发生教学法在高等代数教学中的应用.首先介绍发生教学法的起源,德国动物学家海克尔提出了生物发生律,并运用到数学教育领域,产生了发生教学法;其次阐述发生教学法的策略,要认识教学主题的来龙去脉,掌握发生过程的关键因素,理解会遇到哪些障碍,设计符合认知规律的问题;最后论述如何运用发生教学法实施矩阵运算教学,设计了5个步骤,展示了具体教学过程,说明了设计的理由,为丰富和发展发生教学法提供了参考.
关键词: 发生教学法; 矩阵运算; 数学史; 策略;
Abstract: Taking matrix operation as an example, the application of generative teaching method in advanced algebra teaching has been explored in this paper. Firstly, the origin of generative teaching method has been introduced, and E. Haeckel puts forward the biogenetic law, which is applied to the field of mathematics education to produce generative teaching method. Secondly, the strategy has been expounded of generative teaching method, which is to understand the context of teaching theme, master the key factors of occurrence process and understand the encounter. Finally, it has been discussed how to use the generative teaching method to carry out the teaching of matrix operation, designs five steps, shows the specific teaching process, explains the reason of design, and provides reference for enriching and developing the generative teaching method.
Keyword: generative teaching method; matrix operation; history of mathematics; strategy;
《教育部关于一流本科课程建设的实施意见(教高2019)》指出: “课程目标坚持知识、 能力、 素质有机融合, 培养学生解决复杂问题的综合能力和高级思维. 教学内容体现前沿性与时代性, 及时将学术研究、 科技发展前沿成果引入课程”. 因此我们要积极探索教学新方法, 创新教学新模式, 提高本科教育质量, 培养符合新时代的大学生. 对大学数学教学, 要实现此目标, 必须推行数学教学改革, 增加数学教学难度, 拓展数学教学深度, 把数学课堂变成启迪智慧的场所.
1 、发生教学法的起源
1866年德国动物学家、 进化论者海克尔在论着《生物体普通形态学》中指出: “个体发育是种群成长的迅速而浓缩的重演”, 即生物发生律. 德国哲学家黑格尔首次将生物发生律迁移到认识论, 认为个体的认知发生是人类认识产生、 发展过程的重演. 对于数学教育, 即个体对数学知识的学习过程必须遵循数学知识的客观发生过程. 因此要求教师通过数学的发展过程了解人类是如何获得某些数学认识的, 从而对学生应该如何领悟这些认识作出更好的再创造. 把数学的发展过程作为教学线索, 不具体谈论数学史, 通过数学的发展过程来启示教学, 这就是发生教学法.

2、 发生教学法的策略
发生教学法的目的是通过探索知识的起源, 激发学生的学习动机, 追寻首创者的历史背景, 弄清解决问题的关键因素. 从心理的角度看, 不了解问题的来龙去脉是很难解决问题的. 发生教学法的根基是数学史, 但是数学史仅仅是促进教育, 方便掌握数学知识的素材, 不是历史. 发生教学法借鉴历史引入主题, 保护学生猎奇的天性, 通过引导学生重现知识的再发现过程, 发展学生的创造力, 培养学生的创新精神.
实施发生教学法关键在教师, 要求教师深刻认识教学主题的来龙去脉、 发展过程, 透彻掌握教学主题发生过程中的关键因素、 重要环节, 完全理解从一个阶段发展到下一个阶段的原因是什么?会遇到哪些障碍和困难?为了促进教学, 设计教学主题发展过程的某些关键环节, 设计符合认知规律、 环环相扣的问题[1,2].
3、 发生教学法在矩阵运算教学中的实践
矩阵是高等代数中的一个基本概念, 不仅在数学的各个领域有应用, 而且也是其他理工学科必不可少的数学工具. 因此矩阵运算的教学, 对于后续数学知识、 其他学科知识的学习和应用非常关键. 现以《高等代数》[3]为例, 以大学数学专业的学生为教学对象, 介绍发生教学法在矩阵运算教学中的实施过程.
3.1、 全面了解矩阵的历史
纵观世界数学发展史, 可以发现矩阵思想有两个起源, 即东方以中国为代表, 西方以英国、 德国和法国为代表. 在东方, 中国的《九章算术》大约成书于公元1世纪, 其中“方程”章, 专门研究解线性方程组. 当时用算筹将未知数的系数和常数项排列成一个长方阵, 运用遍乘直除算法求解, 这就是矩阵最早的雏形, 遍乘直除算法就是现今矩阵的初等变换. 以算法体系为特征的中国传统数学, 为世界数学的发展开创了新观念. 在西方, 矩阵思想是随着17、 18世纪科技发展形成的, 矩阵概念正式建立于19世纪的欧洲. 18世纪, 人们研究物理问题时出现了微分方程, 产生了特征值、 特征向量等概念, 这是微分方程研究中孕育的矩阵思想. 18世纪末到19世纪初, 数学家们研究二次型时出现了矩阵的阵列形式. 如德国数学家高斯(1777-1855)将二次型理论进行了系统的推广, 给出了两个线性变换系数矩阵复合的概念, 隐含矩阵乘法思想. 法国数学家柯西(1789-1857)在行列式理论研究中, 涉及到了正定矩阵、 对称矩阵和相似变换等问题. 1850年, 英国数学家西尔维斯特(1814-1897)在研究未知量个数与方程个数不相等的线性方程组时, 遇到行列式不能使用的问题, 于是提出了“矩阵”一词, 他是矩阵的最先使用者. 在1855至1858年间, 英国数学家凯莱(1821-1895)在矩阵方面作了开创性的工作. 在对矩阵零散认识的基础上, 凯莱首先将矩阵脱离行列式与线性变换而作为一种数学对象进行研究, 初步完善了矩阵的知识结构体系, 创立了矩阵初等理论, 引进了矩阵简化记法, 矩阵的理论体系主要体现在他的3篇论文中, 即《矩阵论研究报告》、 《矩阵论研究报告的补充》、 《矩阵方程qQ-Qq′=O》[4].
矩阵初等理论建立后, 许多数学家继续进行矩阵理论的研究. 1861年, 英国数学家史密斯(1826-1883)提出了增广矩阵和非增广矩阵的概念. 1879年, 德国数学家弗罗伯纽斯(1849-1917)给出了矩阵秩的概念. 1884年, 西尔维斯特定义了对角矩阵和数量矩阵. 19世纪末, 矩阵的研究元素已经属于抽象域. 20世纪初, 矩阵理论继续完善, 由一种数学工具, 经过200多年的研究积累成为独立的一门数学理论, 即矩阵论. 目前, 矩阵论又分为矩阵方程论、 矩阵分解论和广义逆矩阵论等矩阵现代理论, 矩阵论已经成为有广泛应用的数学分支.
3.2、 比较矩阵运算与数的运算的关系
矩阵源起于数的思想, 是数的拓展, 即数阵, 但是与数又有区别. 实际上矩阵运算就是一些法则, 按照这些法则将几个矩阵转化为一个新矩阵或数. 从此角度来讲, 矩阵运算与数的运算实质相同. 矩阵运算一般包括加法、 减法、 数乘、 乘法、 乘方、 转置、 逆、 伴随矩阵、 初等变换和方阵的行列式等. 矩阵加法、 减法是通过矩阵的对应元素来进行的, 这与数的加法、 减法一致, 有数的影子, 但是矩阵与数之间又有巨大差异. 表现在: (1)矩阵运算有约束, 矩阵加法、 减法要求两个矩阵的行数、 列数对应相等, 矩阵乘法要求前面矩阵的列数与后面矩阵的行数相同, 矩阵乘方要求矩阵是方阵; (2)矩阵乘法不具备交换律, 即并不是所有的矩阵都满足AB=BA; (3)矩阵乘法中包含数的加法, 因此若矩阵A和B满足AB=O, 但是并不能确定A=O或B=O; (4)矩阵运算与数的运算种类并不完全相同, 矩阵没有除法运算、 开方运算, 矩阵有数乘运算、 转置运算; (5)不是所有非零矩阵都具有逆矩阵, 但是对任意非零数A, 总能找到另一个数B, 使得AB=BA=1. 通过比较, 让矩阵运算建构在数的运算的基础上, 能够形成矩阵运算稳固、 清晰的知识网络.
3.3、 学习矩阵运算的困惑与障碍
大学数学专业的学生, 已经具备数学核心素养, 可以独立地提出问题、 分析问题和解决问题, 经常批判别人的想法. 这样的学生学习矩阵运算, 总会有许多疑问. 如为什么有矩阵运算?为什么要这样定义矩阵运算?怎样使用矩阵运算解决问题?矩阵运算与后续知识有何关系?于是, 关于矩阵运算的教学, 一定要启发学生、 引导学生解决这些问题. 只有学生认识了这些, 学生才能彻底掌握矩阵运算的来龙去脉, 从而有利于学生建构新知识和新思想, 同时也能够让学生明白数学概念的产生并不是无源之水、 无本之木, 数学概念的建立有其自然性、 科学性与必然性, 这样才能有效激发学生的求知欲, 培养学生的创新精神.
3.4 、根据历史, 重构课堂
3.4.1 、创设情境, 引入新知

首先探讨方程组的解法.
有多种方法, 有学生提出将下面x1,x2的表达式分别带入到上面两个方程, 然后整理得到关于y1,y2的二元一次方程组, 求y1,y2的值, 再求x1,x2的值. 现在具体分析这种方法. 带入后得到关于y1,y2的方程组是, 此方程组的系数矩阵是, 而原方程组中上面两个关于x1,x2的方程组的系数矩阵是, 下面两个关于y1,y2的方程组的系数矩阵是, 实际上可以认为矩阵与矩阵的复合得到矩阵. 通过观察可以发现:的第一行元素与的第一列元素通过运算1×2+2×3可以得到的元素8;的第一行元素与的第二列元素通过运算1×4+2×5可以得到的元素14. 依此类推, 可以得到的所有元素. 可以认为乘以得到
矩阵的运算很多, 矩阵思想的萌芽是伴随其他理论研究而出现的. 18世纪前期, 数学家们在研究微分方程解的问题时孕育了矩阵的初步思想, 如柯西进一步研究达朗贝尔提出二阶微分方程时, 产生了特征方程和正交变换等概念. 18世纪中期, 行列式理论的发展催生了矩阵思想的形成, 如艾森斯坦在研究线性方程组复合的问题时, 指出复合的顺序往往不可以改变, 实际上是说明矩阵的乘法不具备交换律. 18世纪末期到19世纪初期, 二次型理论的研究促进了矩阵思想的进一步发展. 如高斯在研究三元二次型时, 给出了3×3矩阵相乘的法则. 实际上, 矩阵思想的产生, 矩阵运算的出现, 都是为了解决问题, 为了书写和运算方便. 数学中的各种概念都不是凭空产生的, 通常是各种具体问题的抽象[5,6].
3.4.2、 借鉴旧知, 建构新知
定义1 数域F上的数k与F上的一个m×n矩阵A=(aij)的乘积kA指的是m×n矩阵(kaij). 数与矩阵乘积的运算叫作数与矩阵的乘法[3]. 如, 但是. 根据行列式的性质,表示2只能乘以行列式中的某一行或某一列的所有元素. 数与矩阵的乘法、 数与行列式乘法有区别. 若A是n阶方阵, 则det(kA)=kndet A.

定义2 两个m×n矩阵A=(aij), B=(bij)的和A+B指的是m×n矩阵(aij+bij), 两个矩阵和的运算叫作矩阵的加法[7]. 显然只有行数相同, 列数相同的矩阵才能相加.
如. 但是, 应该是. 矩阵的加法与行列式的加法有差异.
数与矩阵的乘法、 矩阵的加法实际上最终都是数与数的运算, 根据数的运算律可以得到: 其中A,B和C表示任意m×n矩阵, 而a,b表示任意数.
定义3 A-B=A+(-B), 于是有A+B=C?A=C-B.
矩阵的一些基本思想很早就在数学多个领域出现了, 但只是有矩阵的排列形式没有明确矩阵概念. 在逻辑上, 矩阵的概念先于行列式的概念, 而在历史上次序正相反. 1850年, 西尔维斯特在研究未知量个数与方程个数不相等的线性方程组时, 行列式不能使用, 提出了矩阵一词, 表示一项由m行n列元素组成的矩形阵列, 这是最早矩阵一词的使用. 在矩阵一词使用以前, 凯莱就已经开始探究矩阵的有关知识. 1855年, 凯莱引进矩阵的简化记法. 在1855至1858年间, 凯莱首先将矩阵脱离行列式与线性变换而作为一种数学对象进行了研究, 初步建立了矩阵的知识结构体系, 创立了矩阵初等理论. 1896年, 弗罗伯纽斯给出了凯莱-哈密顿定理的一般性证明, 得到了矩阵秩、 对称矩阵、 特征向量等大量结论. 随着数学家们前赴后继的研究, 20世纪建立了丰富的矩阵现代理论[8,9].
3.4.3、 拓展认知, 突破重点
定义4 数域F上的m×n矩阵A=(aij)与n×p矩阵B=(bij)的乘积AB指的是这样的一个m×p矩阵, 这个矩阵的第i行第j列的元素cij等于A的第i行的元素与B的第j列的对应元素乘积的和: cij=ai1b1j+ai2b2j+…+ainbnj. 两个矩阵只有当第一个矩阵的列数等于第二个矩阵的行数时才能相乘[10].
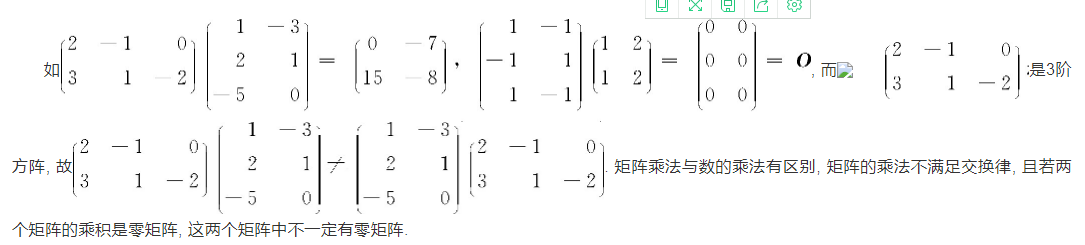
如, 而是3阶方阵, 故. 矩阵乘法与数的乘法有区别, 矩阵的乘法不满足交换律, 且若两个矩阵的乘积是零矩阵, 这两个矩阵中不一定有零矩阵.
定义5k(k是正整数)个方阵A的乘积叫作A的k次方, 记作Ak. 约定A0=I[7]. 这样一个n阶方阵A的任意非负整数次方有意义, (AB)n与AnBn不一定相等(n是正整数), 若AB=BA, (AB)n=AnBn才成立.
下面介绍两类特殊的矩阵. 对于n阶方阵A, 若存在正整数k, 使得Ak=O, 这样的方阵A就叫作幂零矩阵. 对于n阶方阵A, 若存在正整数k, 使得Ak=I, 这样的方阵A就叫作幂么矩阵[11,12].
1801年, 高斯在《算术研究》中, 系统推广了二次型理论, 给出了两个线性变换复合的概念, 复合后的系数矩阵就是原来两个变换系数矩阵的乘积. 1843年, 艾森斯坦在研究线性方程组复合的问题时, 指出复合的顺序不可以改变, 即矩阵乘法不具备交换律, 这是矩阵乘法规则的最早雏形. 由于矩阵乘法在中小学数学中没有相类似的运算, 常使初学者不容易理解. 于是创设情境环节, 通过还原以前人们解决线性方程组复合的问题, 让学生体会矩阵乘法规则的合理性.
3.4.4 、深挖外延, 降解难点
定义6 设m×n矩阵, 把A的行变为列所得的n×m矩阵叫作矩阵A的转置[7]. 矩阵转置的性质有:

矩阵运算一般有加法、 减法、 数乘、 乘法、 乘方、 转置、 逆、 伴随矩阵、 初等变换和方阵的行列式等, 其中矩阵加法、 数乘统称为矩阵的线性运算, 这些运算是将来学习向量空间、 线性变换和二次型等知识的基础. 以后还会不断出现矩阵的新运算, 矩阵理论将逐步发展和完善.
3.4.5、 综合应用, 巩固新知
利用矩阵的运算解决问题.
例1 对任意n阶矩阵A, 求证: 存在n阶矩阵B和C, 使得A=B+C, 且B=BT, C=-CT.
证 不妨设A=(aij)nn, 若令B=(bij)nn,bij=aij+aji2, 则B=BT; 令C=(cij)nn,cij=aij-aji2, 则C=-CT. 而aij=bij+cij(i,j=1,2,…,n), 故A=B+C.
德国数学家弗罗伯纽斯(1849-1917)最早提出此结论, 并给出了证明. 例1有矩阵加法、 矩阵转置, 不仅需要具备较强的计算能力, 而且还需要较强的逻辑推理能力.
本节学习了矩阵的几种运算, 将来还会不断学习矩阵的其他运算. 要将矩阵运算与数的运算、 行列式运算比较, 并通过适当的练习巩固和加深印象, 这样才能深刻掌握各种运算的本质, 灵活运用各种运算, 才能为后续知识的学习作好铺垫.
4 、结 语
矩阵运算是数学专业大一学生学习高等代数的重要内容, 也是中学数学与大学数学衔接的关键知识点, 教学得当能够促进中学数学到大学数学学习的顺利过渡, 实施发生教学法能够实现有效跨越. 运用发生教学法进行矩阵运算教学, 是根据人类认识矩阵运算的实际过程和学生认知特点进行模拟设计, 再现了矩阵运算思想萌芽、 建立和发展的过程, 符合个体认识规律, 有利于新知识建构. 通过矩阵运算与数的运算、 行列式运算的比较, 教师不断启发、 引导学生, 激活学生的思维, 充分体现了以学生为中心的教学目的. 教学中, 有学生探索的过程、 学生抽象概括的过程. 既有合情推理, 也有演绎推理. 通过补充数学史, 使得抽象、 严谨、 冰冷的数学知识变得直观、 形象、 生动, 激发了学生的学习兴趣. 这个过程, 不仅是学生掌握数学知识的过程, 更是学生发展创造力, 培养科学精神的过程. 总之, 发生教学法是有效提高大学数学教育质量, 促进一流本科课程建设的新方法.
参考文献
[1] 张俊忠,綦春霞.发生教学法:起源、 理论基础与应用——以数学教育为例 [J].中学数学杂志,2015(2):1-4.
[2] 汪晓勤.HPM:数学史与数学教育 [M].北京:科学出版社,2017:1-10.
[3] 张禾瑞,郝钅丙新.高等代数 [M].5版.北京:高等教育出版社,2007:177-187.
[4] 李文林.数学史概论 [M].3版.北京:高等教育出版社,2011:200-220.
[5] 朱俊蕾,郭艳凤.基于函数■的高等数学教学探索 [J].西南师范大学学报(自然科学版),2020,45(2):143-148.
[6] 江蓉,王守中.向量组线性相关性的教学设计 [J].西南师范大学学报(自然科学版),2017,42(4):146-147.
[7] 孟道骥.高等代数与解析几何(上册) [M].2版.北京:科学出版社,2007:100-120.
[8] 贺书文,商彦英.一类带有周期位势的分数阶耦合系统的正基态解 [J].西南大学学报(自然科学版),2019,41(2):64-69.
[9] 王娇凤,王震.三阶三系数偏差分方程的振动性 [J].西南大学学报(自然科学版),2019,41(7):83-87.
[10] 北京大学数学系前代数小组.高等代数 [M].4版.北京:高等教育出版社,2013:61-75.
[11] 陈景良,陈向晖.特殊矩阵 [M].北京:清华大学出版社,2001:90-99.
[12] 程云鹏.矩阵论 [M].2版.西安:西北工业大学出版社,1999:50-70.





