摘 要: 高等数学课程中极限的学习既是重点也是难点, 尤其是对极限思想的理解, 更是贯穿了高等数学的整个学习。本文旨在对极限的概念进行分析, 从数列和函数两方面剖析无限逼近思想的应用, 最后给出极限相关的典型例题, 从根本上解决极限思想的理解难和认知难问题。
关键词: 高等数学; 极限; 数列极限; 函数极限;
高等数学是大学课程教育体系中的一门基础课程, 更是医学院校部分专业必修课程。而数学本身的抽象性和系统性以及医学专业的自身需要 (如专业课程繁多, 课程任务重, 公共基础课学时少等) , 让高等数学这门课程的学习变得更加困难。高等数学课程由极限, 连续, 微分和积分四大块组成, 其中的极限思想和极限方法又是贯穿整个高等数学的主线, 极限的学习是连续的基础, 同时又间接贯穿着微分和积分的概念, 因此想要更好地学习高等数学后续章节, 就必须重点掌握极限的概念。本文将针对医学专业学生实际, 对极限的概念进行一定的探讨和总结。
一、极限的概念
极限的本质是在一种函数关系中观察当自变量在发生变化时, 函数值会有什么样的变化。如果给定自变量一种变化趋势, 函数值相应的趋近于一个固定的值, 那么其中就蕴含着极限的定义。极限分为数列极限和函数极限两大类, 二者无论是从概念上还是从具体问题的求解上都既有区别又有联系。
(一) 数列极限
数列的本质也是一种特殊的函数关系, 即f (n) =an, 只是由于数列本身的特点, 在这种函数关系中, 自变量的取值不是连续的, 而是一个个离散的整数点, 即定义域表现为正整数集。因此, 考虑数列an的极限就只有一种方式--即下标n的变化单方向的趋近于无限的增大, 所以即便符号是n→∞, 也只有一种情况。

定义1:对数列{a n}, 当f (n) =an中作为自变量的n无限趋近于+∞时, 如果数列中每一项an的值都无限的接近于某一个固定的常数A, 那么称数列an是收敛的, 并且收敛于极限值为A, 否则称数列an为发散的。
(二) 函数极限
在函数y=f (x) 中观察自变量变化时, 函数值的变化。与数列不同, 对一般函数而言, 自变量x的取值可以是全体实数集R中的任意一个值, 那么相应的自变量的变化趋势与数列中下标n的变化趋势相比就有了多种情况。
1. 自变量x→∞时的极限
由于函数y=f (x) 中, 自变量x的取值是在R中取得, 所以自变量在趋近于无穷的变化趋势中, 当指的是无穷时就包含了两个方向:正无穷+∞和负无穷-∞。
定义2:设函数在 (b, +∞) 内有定义, 当自变量x的取值无限增大时, 若函数值f (x) 的变化无限接近于某一个固定的常数A, 那么称函数f (x) 在时收敛, 且收敛于极限值A。
定义3:设函数在 (-∞, a) 内有定义, 当自变量x的值无限减小时, 若函数值f (x) 的变化接近于某一个固定的常数A, 那么称函数f (x) 在x→-∞时收敛, 且收敛于极限值A。
定义4:若函数f (x) 在全体实数集R上有定义, 当自变量x的绝对值无限增大时, 函数值f (x) 的变化接近于某一个固定的常数A, 那么称函数f (x) 在x→∞时收敛, 且收敛于极限值A。
结合定义2, 定义3和定义4不难发现, 若想f (x) 在x→∞的极限值存在必须要求函数f (x) 在和x→-∞的极限同时存在并且极限是相等的, 这样才能合并成为lxi→m∞f (x) =A。
2. 自变量x→x0时的极限
在这种情况中, 针对函数y=f (x) , 由于自变量的取值是在实数集中取得, 而由于实数本身的稠密性----即任意两个实数之间都包含有无穷多个实数, 因此, 函数的极限就会产生一种数列极限不会包含的情况, 即在定义域中某一点0x处取极限。
正是由于任意两点间都含有无穷多个数, 所以自变量在靠近某一点x0时, 就可以出现一种经过无数个点之后过渡到x0, 产生一种无限逼近的趋势。同时由于自变量的取值是在一维的实数轴上取得, 因此自变量x在靠近x0时就会产生两种方向, 从x0的左侧无限靠近x0以及从x0的右侧无限接近x0。
定义5:函数f (x) 在x0的某一左邻域内有定义, 若自变量x在x0的左邻域内无限靠近x0时, 函数值函数值f (x) 的变化接近于某一个固定的常数A, 那么称函数f (x) 在x→x0-时是收敛的, 即函数在x0处有左极限值A。
定义6:函数f (x) 在x0的某一右邻域内有定义, 如果自变量x在x0的右邻域内无限靠近x0时, 函数值函数值f (x) 的变化接近于某一个固定的常数A, 那么称函数f (x) 在x→x0+时是收敛的, 即函数在x0处有右极限值A。
定义7:函数f (x) 在x0的某邻域内有定义, 若自变量x在定义域内无限靠近x0时, 函数值函数值f (x) 的变化接近于某一个固定的常数A, 那么称函数f (x) 在x→x0时是收敛的, 即函数在x0处有极限值A。
显然, 若要求函数f (x) 在x0处有极限, 必须要求函数在该点处左极限和右极限都存在并且极限值相等, 这样才能合并为该函数在0x处极限值是存在的;反之, 如果左极限和右极限中有一个是不存在的或者两个极限值都存在但不相等, 那么函数f (x) 在x0处极限就是不存在的。
二、典型例题
(一) 数列极限的例题

(二) 函数极限的相关例题

解:函数f (x) =arctanx的函数图像
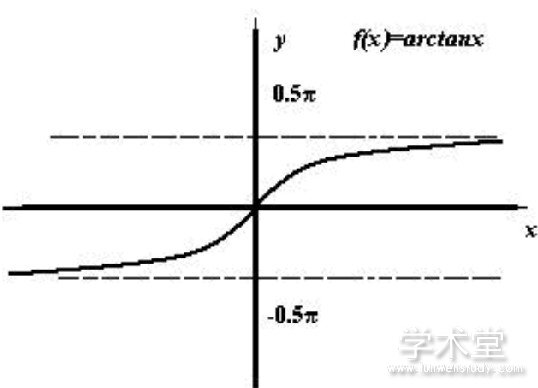

通过以上对极限概念包括数列极限和函数极限的分析, 指出了极限概念的本质所在, 即自变量变化时函数值的变化趋势;同时也点明数列极限与函数极限不同的根本原因, 帮助学习者从本质上理解极限的无穷逼近思想;最后列举一些极限中使用基本方法的典型例题, 帮助进一步理解极限概念, 为接下来连续, 导数, 微分和积分的学习做好基础。
参考文献:
[1] 马建忠.医用高等数学[M].北京:科学出版社, 2013.
[2] 马建忠.医用高等数学学习指导与习题全解[M].北京:科学出版社, 2015.
[3]顾作林.高等数学[M].北京:人民卫生出版社, 2016.
[4]廖红菊.求极限的方法与技巧[J].湖北广播电视大学学报, 2010 (10) :148-149.





