
1 评价方法
1. 1 因子分析模型
因子分析是通过原始数据相关系数矩阵内部结构的研究,将多个指标转化为少量互不相关且不可观测的随机变量( 即主因子) ,以提取原有指标绝大部分信息的统计方法. 当因子载荷矩阵结构不够简化时,可以通过因子旋转使因子具有更为鲜明的实际意义,同时使用因子得分函数对样本给出相应的评价和排序.设有 n 个样品,每个样品观测 p 个指标( 变量) ,X1,X2,. . . ,XP,得到原始数据矩阵 X=( X1,X2,…,XP)T. 因子分析的数学模型为X=AF+ε,其中,F=( F1,F2,…,Fm)T为X 的公共因子,A 为因子载荷矩阵,ε 为特殊因子.论文使用主成分因子提取方法,其特点在于可以用方差贡献值 βi衡量第 i 个公因子的重要程度.1. 2 因子分析具体步骤。。
将原始数据标准化,为书写方便,仍为 X. 为了使综合评价的结果客观、合理,必须消除数量级和量纲不同带来的影响. 采用标准化处理,建立指标的相关系数矩阵 R; 计算特征方程 R-λE =0,得到相关系数矩阵R 的特征根 λ1≥λ2≥. . . ≥λp≥0,μ1,μ2,. . . ,μp为相应的标准正交化特征向量; 根据累计贡献率的要求,譬如 Σmi = 1λi/ Σpi = 1λi≥85% 时,取前 m 个主成分代替原来的 p 个指标,计算因子载荷矩阵 A; 对 A 施行方差最大正交旋转,建立因子模型的目的不仅在于找到公共因子,更重要的是知道每一个公共因子的意义; 对主因子进行命名和解释,如需进行排序,则计算各个主因子的得分 Fi= αix,以贡献率为权重,对 Fi加权计算综合因子得分.
2 实证分析
2. 1 消费水平评价指标与数据
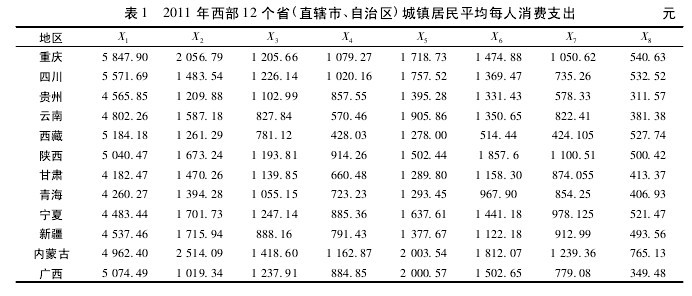
选取了反映城镇居民综合消费水平的 8 个指标,分别为 X1人均食品支出( 元/人) 、X2人均衣着支出( 元/人) 、X3人均住房支出( 元/人) 、X4人均家庭设备及服务支出( 元/人) 、X5人均交通和通信支出( 元/人) 、X6人均文教娱乐用品及服务支出( 元/人) 、X7人均医疗保健支出( 元/人) 、X8其他商品及服务支出( 元/人) . 应用多元统计学中的因子分析法,选取中国统计年鉴中 2011 年的数据,对中国西部地区包括重庆、四川、贵州、云南、西藏自治区、陕西、甘肃、青海、宁夏回族自治区、新疆维吾尔自治区、内蒙古自治区、广西壮族自治区等经济情况进行实证分析.【表1】
2. 2 判断数据是否适合因子分析
各变量应该具有相关性,如果变量间彼此独立,则无法从中提取公因子,也就谈不上因子分析法的应用. 在 SPSS 中,KMO和球形 Bartlett 检验用于因子分析的适用性检验,可以通过Bartlett 球形检验来判断,如果相关阵是单位阵,则各变量相互独立,因子分析法无效. KMO 检验用于检查变量间的偏相关性,取值在 0 ~ 1 之间,KMO 统计量越接近 1,变量间的偏相关性越强,因子分析的效果越好; 当 KMO 统计量在 0. 5 以下时,不适合应用因子分析法,应考虑重新设计变量结构或者采取其他统计分析方法. 表 2 给出了因子分析 KMO 和 Bartlett 的检验结果. 得知,原变量适合进行因子分析.【表2】

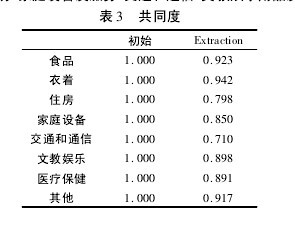
变量共同度是表示各变量中所含原始信息能被提取的公因子所表示的程度. 由表 3 可知,几乎所有变量共同度都在 80%以上,因此,提取出的这几个公因子对各变量的解释能力是较强的.【表3】
2. 3 因子分析的数据结果及分析
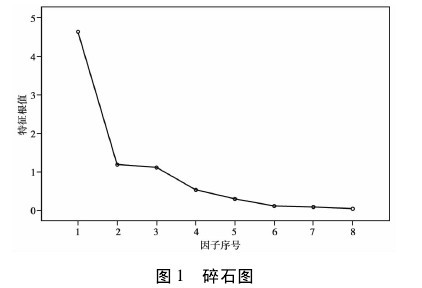
图 1 被称为碎石图,用于显示各因子的重要程度,其横轴为因子序号,纵轴表示特征根大小. 它将特征根从大到小排序,从而,可以很直观地看出哪些是主因子.【图1】
按照特征根大于 1 的原则,选入 3 个公共因子,其累计贡献率为 86. 598%,特征根及累计贡献率见表 4.表5 为建立的因子载荷阵. 此时得到的未旋转的公共因子的实际意义不好解释,为此,对公共因子施行方差最大化正交旋转,表6 为经旋转得到的因子载荷阵,表7 为因子载荷阵通过方差最大化正交旋转后得到的各主因子的方差贡献率. 由旋转后的因子载荷阵表6 可观察出,第三主因子 F3仅在 X1( 人均食品支出) 上的载荷较大,在此因子上的得分反映了人们最基础的消费情况; 第二主因子 F2在 X2( 人均衣着支出) 、X8( 其他商品及服务支出) 上的载荷较大,在此因子上的得分反映了生活水平的提高; 第一主因子 F1在 X3( 人均住房支出) 、X4( 人均家庭设备及服务支出) 、X5( 人均交通和通信支出) 、X6( 人均文教娱乐用品及服务支出) 、X7( 人均医疗保健支出) 上的载荷值较大,主要反映了生活消费水平进一步的提高. 随着西部大开发,经济的快速增长,人们在住房、家庭设备及服务、交通和通信、文教娱乐用品及服务及医疗保健方面的消费越来越高.
2. 4 因子得分和综合得分
以各公共因子的方差贡献率占 3 个公共因子总方差贡献率的比重作为权重进行加权汇总,得出各地区的综合得分情况,并且进行排名. 综合得分模型:【1】
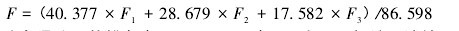
3 结 论
对各地区在 3 个公共因子上的得分进行加权综合,就得到了综合得分. 再根据统计软件 SPSS 进行 ward聚类分析,由综合得分评价西部地区的城镇居民的消费水平,结果如表 9.我国西部地区幅员辽阔,各个省份( 直辖市、自治区) 生产力发展水平、人口状况、地理环境、民族构成、交通设施的差异很大,各地区受地域特征和历史文化不同所形成的消费观念和消费习俗不同,形成了各个地区消费水平不平衡的显着特征. 通过了解各地区的消费水平,可以采取相应的发展策略和技术水平,制定扩大居民消费、拉动地方经济发展的政策措施,这便是进行区域划分要解决的问题.
参考文献:
[1]克劳斯. 巴克豪斯,本德. 埃里克森,伍尔夫. 普林克. 多元统计分析方法: 用 SPSS 工具[M]. 上海: 格致出版社,2009
[2]方开泰. 实用多元统计分析[M]. 上海: 华东师范大学出版社,1989
[3]张尧庭,方开泰. 多元统计分析引论[M]. 北京: 科学出版社,1982
[4]国家统计局. 中国统计年鉴 2012 [M]. 北京: 中国统计出版社,2012
[5]徐科,张艳. 重庆各区县经济发展水平的因子分析[J]. 重庆工商大学学报: 自然科学版,2012,29( 1) : 42-47





