
成本-效用分析作为药物经济学研究的方法之一,在国内外卫生评估中的应用日益普遍。质量调整生命年是计量效用的常用单位,其计算的关键在于生命质量权重即健康效用值的测量。在大多数情况下,使用基于偏好的普适性效用量表来产生健康效用值都是适用的,但也有一些情况下,其表现出灵敏度低的弱点,且普适性的特点往往与临床实际的健康状态关联性差。一些临床研究人员更愿意使用贴近实际疾病的疾病特异性量表或其他健康状态量表测量健康相关生命质量,但是这些非基于偏好的测量量表缺少效用积分体系,无法获得能够用于成本效用分析中的单一的效用指数。而映射法便能解决这类问题,它能够将生命质量测量工具转化成效用指数从而拓展其应用范围。文章将对映射法进行系统介绍,并进一步地对其应用于效用值测量时模型的选择及应用加以分析。
1、映射法的概念及基本原理
映射法可以分为专家法模式和统计学模型分析法模式。由于专家法过于“武断”且争议较大,目前统计学模型分析模式较为理想。在应用时,其需要一个真实的数据集,且两种量表必须同时应用于同一个研究人群。
映射是指非效用值测量方法(包括非基于偏好的条件特异性测量方法和特定的基于偏好的测量方法)对基于偏好且具有效用积分体系的效用值测量方法的映射,它通过估计两种测量方法的相关关系,将非偏好信息转化为同等效力的基于偏好的单一指数。首先,运用回归方法建立回归方程,拟建一个效用值转换模型,方程的自变量为非效用值测量方法的某一类指数,因变量为基于偏好且有积分体系效用值测量方法中的指数;然后对所建立的回归方程进行拟合度的检验;最后,运用模型来预测非效用值测量方法的效用值。
2、映射法的适用情况
2.1疾病特异性量表与基于偏好且具有效用积分体系的健康效用测量量表间的映射
需要对临床试验进行经济性评价时,搭载临床数据收集用于效果测量的经常会是非基于偏好的条件特异性测量方法,如西雅图心绞痛量表等。此时可以运用映射法将特异性测量方法的测量结果转化为基于偏好且有积分体系的测量方法的结果,如欧洲五维健康量表 (euroqol-5D, EQ-5D),从而得到效用值进行成本-效用分析。
3个主要的基于偏好的健康效用表为EQ-5D、健康效用指数 (health utilities index, HUI2、HUI3)和六维健康测量量表(short form-6D, SF-6D)。其中,HUI、EQ-5D和SF-6D已有自身的效用积分体系,能够通过基于偏好的估算方法获得效用值。
2.2普适性量表与基于偏好且具有效用积分体系的健康效用测量量表间的映射
研究者不想要限制证据基础而希望通过临床研究获得综合性数据时,往往需要选择普适性的效用测量方法 (如SF-36、SF-12等)。此时映射法也可以被用于将此类量表的测量结果转换为通过效用积分体系估计得到的健康效用值,进一步进行成本-效用分析。在应用映射法时,临床试验为最佳的数据来源,样本选择可以是社区人口、医院人口以及基层医疗人口。
3、映射法的模型选择
3.1对应于变量及参数类型的总体模型类型
将映射中所使用的非基于偏好的效用量表称为起始量表,将最终映射到的具有效用积分体系、基于偏好的效用测量量表称为目标量表。
在映射之前,需要设立几个假设以作为模型的选择条件:
假设a:起始量表的条目等级能够用于表示一个等距量表的偏好,其中l表示最差健康状态、i表示最佳健康状态;假设b:起始量表维度中的条目拥有相等的权重;假设c:起始量表的维度能够包含与环境和治疗相关的所有健康维度;假设c’:起始量表和目标量表的维度均能够包含与环境和治疗相关的所有健康维度;假设d:起始量表的几个维度之间权重相等;假设e:起始量表定义的最差健康状态为死亡;假设f:起始量表定义的最佳健康状态为完全健康。
从整体来看,自变量应分为两方面。一个是起始量表自身对目标量表结果的影响,另一个为受访者人口学资料特征对目标量表结果的影响。根据量表的设计情况,起始量表自身对目标量表结果的影响共有以下六类总体模型:B=α+β×A+u 式1式1(模型1)是一类最简单的加性模型,其需要满足假设a、b、c’和d。其中,自变量A为起始量表的总分,因变量B为目标量表的效用指数(下同),u为扰动项(下同),即将目标测量方法如EQ-5D回归到起始测量方法如SF-36、HAQ等的总分上。

式4(模型3’)中,是式3(模型3)的补充,其在类型3的基础上,增加了交互作用项作为额外的自变量。但是,并非所有的条目间的交互作用项都能够作为式4的自变量,只有通过以下两个条件筛选得到的交互作用项才能作为自变量:(1)自变量估计系数的符号应为正,即若某一维度中的水平是不太健康的,那么选择其将增加负效用值的大小,例如高的等级应该对应更好的生命质量以及更大的EQ-5D指数;(2)自变量估计系数的显著性P值应小于0.01。与式3相同,此类型需满足假设a和c’,Ax、Ay均为起始量表各条目等级。
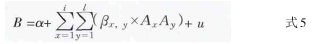
式5(模型4)中,自变量Ax.y表示起始量表条目x的等级y,i为条目个数,l为各条目的等级个数。Ai.l为一个虚拟的离散变量,Ai.
l 是条目i的子集,当健康状态中的第i个条目处于第j个水平时,Ai.
l=1,否则,Ai.
l=0。并非所有的Ai.
l 均能作为自变量,子集的选择同样按照上面的两个规则:
(1)估计量的符号为正;(2)P值小于0.01。式5只需要满足假设c’。
式2、3、5通过包含维度、条目和交互作用项的平方项从而放宽了简单加性模型的假设条件。这三类模型中的维度和条目得分被视为连续型变量,条目应答被模拟为虚拟的离散变量。式5的自变量条目应答能够产生大量的自变量(例如SF-36可以产生多于100个的自变量),有利于对模型中所包含的条目进行筛选。
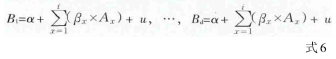
6式6(模型5)是将目标量表的d个维度回归到起始量表的条目等级上,对每个维度的回归作用均要进行估计,其只需满足假设 c’。此类模型无法用于产生预测值,且代表模型性能的拟合优度无法测定,因此,模型5只是用于为模型6自变量的选择提供依据。
B1=α+βi×Ai+βj×Aj+…+βn×An+u,…,Bd=α+βi×Ai+βj×Aj+…+βn×An+u 式7式7(模型6)是将目标量表的d个维度回归到起始量表的条目等级的子集上,其根据式6的结果来选择子集,选择规则与式5中的相同。同样,式7只需要满足假设c’。
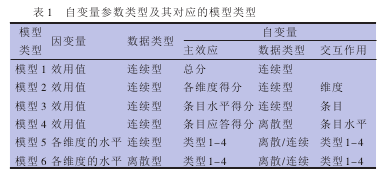
式6、7是更为复杂的两种模拟关系的途径。它们对目标量表的各个维度单独进行估算。如果目标测量方法为EQ-5D,相较于式6中的连续型,式7中将因变量定义为离散型更为精确、恰当。六类模型的变量指标及其分别对应的数据类型详(表1)。
3.2常用的映射模型
3.2.1普通最小二乘法。普通最小二乘法 (ordinary least square,简称OLS)是一种基本的用于参数估计的线性回归模型,在计量经济学中使用广泛。其基本原理为通过最小化误差的平方和寻找数据的最佳函数匹配。
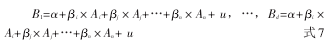
若起始量表及目标量表的量表属性符合上述总体模型1、2、3,则在映射时均可以选择OLS作为具体的预测估计模型选择。此时,起始量表的总得分、维度得分以及条目等级得分均可作为自变量,此外,还可以加入模型4中的虚拟变量即每个条目等级的子集。
3.2.2 Tobit模型。在医学实际中往往会遇到一些删尾数据。例如,健康效用数据通常显著地呈现出一种部分个体达到上限值1的截断效果,致使EQ-5D效用指数得分表现出一种天花板效应,同样的,HUI也存在此类情况。因此,忽略基于偏好的HRQL得分的有界性质而使用传统的线性回归模型(例如OLS)进行映射往往会导致估计出现偏倚以及不一致性。然而,Tobit模型能够为此类数据提供一致且有效的估计手段。
Tobit模型是由Tobin首次提出的,也称截取回归模型,其对连续型但受限或被截断的因变量进行回归分析。
具体来说,上限为1.0的删尾数据的Tobit模型定式为:
即假设有潜在的HRQoLYi*(*为实际观测值) 满足Yi*=Xi×β +εi*,且εi*~ N(0,σ2 )。Yi表示目标量表的健康效用指数,Xi表示影响效用指数的自变量,即起始量表中的相应指标。对 Yi*进行观察,当 Yi<1.0时,Yi= Yi*,否则,Yi=1.0。
运用Tobit模型进行映射,优点在于当误差项满足方差齐性时,与OLS相比,Tobit模型具有更小偏倚。
但是,在不满足方差齐性时,Tobit模型会产生估计偏倚从而误导结果。
3.2.3最小绝对离差模型
CLAD。为解决Tobit模型对于非方差齐性的不适用问题,Powell提出了针对Tobit模型的截断最小绝对离差CLAD模型。由于不要求分布及误差同方差性假设且对删尾数据表现稳健,即使在面对异方差性、非正态性和删尾数据时,CLAD估计法也能够进行估计。其基本思想是通过最小化误差项的绝对值之和来获得回归系数的估计值。
与Tobit模型相同,CLAD也假设HRQoL的测量值设限为1。但相对于Tobit模型侧重于算术平均数、取最小平方和,CLAD模型则侧重于中位数、取最小绝对离差和。

值得注意的是,Tobit模型和CLAD估计方法都是假设效用用于观察不够理想,从而对HRQoL进行的模拟。
3.2.4多分类逻辑回归。当因变量为离散变量(例如EQ-5D的各维度水平),自变量为分类变量时,相比于上述几种模型,选用多分类逻辑回归模型进行映射更为适合。此种模型能够产生维度水平的概率分布,之后可以运用蒙特卡洛程序从分布中选择一个单一水平,并将其输入模型来计算应答者的单一指数值。
多分类逻辑回归 (multinomial logistic regression)是研究多分类资料观察结果与一些影响因素关系的多变量分析方法,它是二分类逻辑回归的扩展,适用于应变量为无序分类的资料 。 假设应变量Y(Y1,Y2,…,Yn) 为一个包括n个类别的无序多分类变量,X (X1,X2,…,Xm) 为影响Y的m个自变量,那么其多分类逻辑回归模型可表示为:

式10中,对于包括n个类别的应变量Y,得出的多分类逻辑回归就包括n-1个方程。
β0i为第i个方程的常数项,β1i,β2i,…,βmi逻辑为第i个方程自变量X1,X2,…,Xm的回归系数。
这种模型是对目标量表的每个维度分别进行估计,而不是对其自身的单一指数。根据各个维度的应答估计的选择值集合,可以定义一个健康状态以及其应对应的一个指数得分。上述指数得分不是直接处理的,因此这种模型的优点在于其能够有效避免上述指数得分的分布问题,也更符合EQ-5D量表的逻辑。此外,由这种基于维度方法衍生出的算法能够应用于可获得本国值集合而无须换算的国家。相反,OLS和CLAD等直接预测模型需要换算。
3.3映射模型性能的评价
3.3.1模型的解释能力评价。模型的解释能力即拟合优度一般通过拟合优度R2和调整R2(adjustedR2)来表达。R2是模型中解释变量或回归元个数的非减函数,其统计量能够量化在因变量Y的总变异中由回归模型解释的那个部分所占的比例。调整R2是指对R2方程中的平方和所涉及的自由度进行调整。拟合优度R2和调整R2越大,说明构建出的模型拟合优度越好。
3.3.2模型的预测能力评价。模型的预测能力是指模型预测值与实际测量值之间的偏差。其中,总体的预测能力用平均误差 ME (mean error) 和平均方差 MSE(mean squared error)表示;个体水平的预测能力用平均绝对误差MAE (mean absolute error) 表示,即预测误差大于0.1和0.05的状态数。上述指标的结果值越小,表示模型的预测能力越好。除上述几个重要指标外,运用个体估计的均值、标准差、最大值及最小值等基本描述性统计量也可以衡量模型的预测能力。在模型检验时,应绘制EQ-5D指数的模型预测值与实际测量值的散点图。同时,还应计算预测值范围以及实际测量值与预测值的Pearson相关系数。
4、讨论
非基于偏好的健康测量量表对具有效用积分体系的效用量表的映射模型时主要有OLS、Tobit、CALD、多分类逻辑回归等多种模型,但其是没有一个固定形式的。在实际的研究中,应注意以下几点:(1)应考虑多种备选模型,针对具体量表的结构及参数的逻辑关系和实际含义来选择、取舍模型;(2)应灵活设置变量,必要时还可将各维度水平的交互项加入到模型中,从而更好地控制相关性;(3)在评价模型性能时,应结合模型自身的性能特点,选择适当的评价指标。
总体来说,映射是一种有效的效用值转换方法。因此,在未来的生命质量测量时,应加大力度推广此种方法的应用,这将有助于生命质量研究的深入和发展。
参考文献:
[1]刘利.成本效用分析中效用值测量方法的应用研究[D].北京:北京中医药大学,2012.





