探索IVE方法估计测流不确定度的性能(2)
时间:2017-06-19 来源:水科学进展 作者:白直旭,黄艳,许月萍 本文字数:8326字
因此,国标的测流总不确定度表示如下:
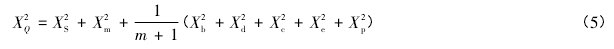 为确定式( 5) 中 Xm、Xe、Xp的大小,国标要求对测区内具有测站代表性、测验条件适宜试验的水文站进行误差试验[7].通过Ⅰ型误差试验分析确定测速历时不足引起的不确定度 Xe; 通过Ⅱ型误差试验确定垂线测点不足引起的不确定度 Xp; 通过Ⅲ型误差试验确定垂线数目不足引起的不确定度 Xm.由此可见,国标确定测流不确定度的方法需要消耗大量的时间及人力物力,并且随着河流条件的改变,需要不定期重新进行试验。
为确定式( 5) 中 Xm、Xe、Xp的大小,国标要求对测区内具有测站代表性、测验条件适宜试验的水文站进行误差试验[7].通过Ⅰ型误差试验分析确定测速历时不足引起的不确定度 Xe; 通过Ⅱ型误差试验确定垂线测点不足引起的不确定度 Xp; 通过Ⅲ型误差试验确定垂线数目不足引起的不确定度 Xm.由此可见,国标确定测流不确定度的方法需要消耗大量的时间及人力物力,并且随着河流条件的改变,需要不定期重新进行试验。
1. 2 插值方差估计法。
Cohn 等[13]于 2012 年提出的 IVE 方法,利用测深和测速时的平均绝对不确定度来计算测流不确定度。下面介绍 IVE 方法如何确定测深的不确定度,测速不确定度的确定方法与测深类似。
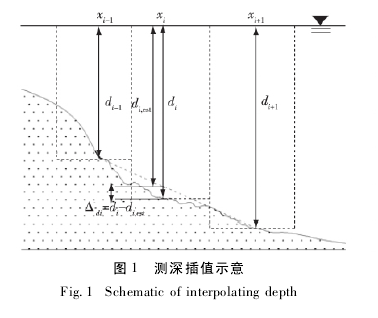 在流速-面积法中,用垂线上的一次测量来代表所求部分的平均水深是测深不确定度的主要来源之一,如图1 所示。实际水深 di等于真实的平均水深 D( xi) 与误差 εi之和,即:
在流速-面积法中,用垂线上的一次测量来代表所求部分的平均水深是测深不确定度的主要来源之一,如图1 所示。实际水深 di等于真实的平均水深 D( xi) 与误差 εi之和,即:
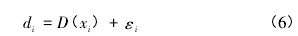 因此,通过与第 i 条垂线相邻的垂线( 即第 i-1 条和第 i+1 条垂线) ,可以得到第 i 条垂线位置上的水深线性内插值 di,est的计算公式如下:
因此,通过与第 i 条垂线相邻的垂线( 即第 i-1 条和第 i+1 条垂线) ,可以得到第 i 条垂线位置上的水深线性内插值 di,est的计算公式如下:
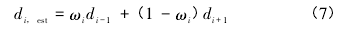 式中:
式中: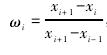 ,xi为第 i 条垂线到测宽起始点的距离。
,xi为第 i 条垂线到测宽起始点的距离。
令 Δdi等于式( 6) 减去式( 7) ,则:
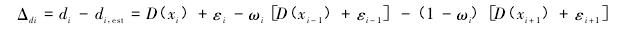 值得注意的是,Δi与测量误差之间存在正相关关系。
值得注意的是,Δi与测量误差之间存在正相关关系。
di与 di,est的数学期望等于真实的平均水深,因此,Δdi的数学期望值等于 0,即:
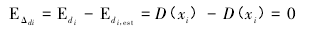 Δdi的方差为:
Δdi的方差为:
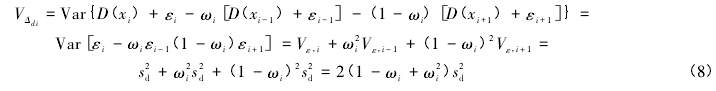 式中: sd为测深的标准差。
式中: sd为测深的标准差。
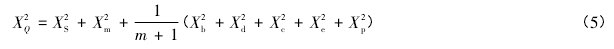
1. 2 插值方差估计法。
Cohn 等[13]于 2012 年提出的 IVE 方法,利用测深和测速时的平均绝对不确定度来计算测流不确定度。下面介绍 IVE 方法如何确定测深的不确定度,测速不确定度的确定方法与测深类似。

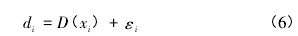
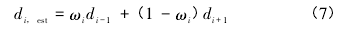
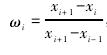 ,xi为第 i 条垂线到测宽起始点的距离。
,xi为第 i 条垂线到测宽起始点的距离。令 Δdi等于式( 6) 减去式( 7) ,则:
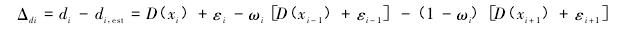
di与 di,est的数学期望等于真实的平均水深,因此,Δdi的数学期望值等于 0,即:
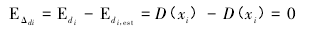
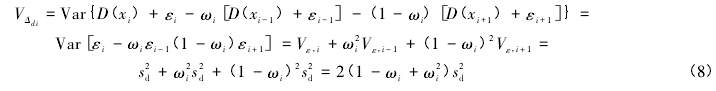
- 相关内容推荐
相近分类:
- 上一篇:河岸带水文对土壤磷素含量分布的影响探究
- 下一篇:三江源区径流对降水的响应及地区差异
推荐阅读





