
1、 前言
节流机构是制冷系统中最重要的部件之一节流机构与蒸发器、制冷压缩机和冷凝器的良好匹配将直接影响制冷系统的工作效率和实际性能。因此对节流机构流量系数的研究一直是相关领域的一个研究热点。由于毛细管结构简单、成本低廉,在小型制冷系统中常用毛细管作为节流机构,但毛细管节流元件存在着流量的自调节能力较弱等问题,毛细管的性能优劣与设计计算相关度较大,因此在毛细管的流量特性研究中计算模型的研究尤为重要。
毛细管流量特性的计算模型,传统上采用基于流体力学的数学和物理模型,随着计算机数值模拟和仿真技术的发展,许多新的研究方法应用于毛细管流量特性的研究,张春路与丁国良等人采用多层前向人工神经网络作为关联模型来辨识绝热毛细管的流量特性,并且得到了比传统思路绝热毛细管流量特性关联模型更好的关联精度。现有毛细管流量特性神经网络研究方法大多采用 BP 神经网络,BP 网络训练常用基于梯度信息的学习算法,误差函数根据神经网络权值的梯度进行修正,BP 算法的初始权值是随机生成的,而不同的初始权值对网络训练精度有很大影响。针对 BP 神经网络对初始权值敏感的问题,有研究结合讨论了遗传算法与神经网络相结合的可行性并且将遗传算法 - 神经网络模型应用到实际应用中但是将该方法应用到毛细管流量特性预测的研究未见报道,因此拟采用遗传算法对流量特性神经网络关联模型的初始权值与阈值进行优化,以期得到更好的关联精度以及更快的关联速度。
2、 基于神经网络和遗传算法的毛细管流量特性关联模型
建立毛细管流量特性的神经网络关联模型需要考虑以下几个主要方面: 神经网络的输入与输出参数、隐层数与隐层神经元数、学习与检验样本以及学习算法等。
2.1输入与输出参数
参数的选择由研究目的决定,本文研究毛细管流量特性,因此选取毛细管的质量流量作为人工神经网络的输出参数。神经网络的输入参数取决于研究对象的特性。对于一定的制冷工质,影响毛细管流量特性的主要因素有四个: 毛细管内径、管长、冷凝压力、进口过冷度。其他的一些相对次要的影响因素在工程应用中通常被忽略不计。由于在正常情况下毛细管的进口为液体制冷剂,故本文暂不考虑进口为汽液两相的情况。
2.2与隐层神经元数的确定
前人的研究成果表明: 只要隐层神经元数充分多,用三层前向网络可以逼近任何闭区间内的一个连续函数; 另一方面,隐层数越多,误差传递环节就会增加,导致神经网络的泛化性能下降,因此,本文首先考虑采用三层前向网络进行数据关联。隐层神经元数直接影响神经网络的学习效果学习速度、精度和泛化性能) 和表现能力。网络神经元数增多时,运行速度变慢,表现能力加强; 网络神经元减少时,运行速度加快,表现能力减弱。
由于神经网络学习的样本一般都带有测量误差或计算误差,为追求高精度而采用过多的隐层神经元反而会导致神经网络的学习效果下降。目前已有较多的方法用于确定隐层神经元数,但是最可靠的方法还是试凑法,这一方法的效率较低,适用于网络规模较小的情况,因此对本文研究是合适的。
通过试凑法确定最佳神经元数为 5,即本文采用的网络结构为 4 -5 -1; 第一层为输入层,输入量为 D、L、、分别表示毛细管内径、管长、冷凝温度、进口过冷度; 第二层为隐层,传递函数选用非线性对数 S 型函数(Logsig) ; 第三层为输出层,输出值为 m,表示质量流量。
表示输入层第 j 神经元对隐层 i 神经元之间的权重表示输出层与隐层之间的权重为隐层的阈值为输出层的阈值。

2.3学习与检验样本
由于本文研究侧重于方法的研究和比较,需要较多的一致性好的样本,故采用由通用模型生成的计算数据作为人工神经网络的学习和检验样本。在本文的研究中,采用的制冷工质有和 R410A 四种,选择 D. Jung 模型计算质量流量。Jung 关联式适用于以下条件⑴制冷剂⑵内径⑶入口流通面积收缩比⑷冷凝温度: 40℃ ~55℃⑸过冷度: 0℃ ~5℃⑹单管质量流量⑺出口条件: 壅塞状态。
质量流量计算式如下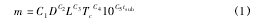
其中参数见下表 1。

输入的各参数见下表 2。

按照表 2 所示参数组合选择样本,每种制冷剂的样本数是 336,任取其中的 200 组作为训练样本,剩余 136 组为检测样本。
2.4学习算法
人工神经网络采用的模型多为经典的反向传播算法,为提高网络收敛速度,研究者们进行了许多改进,提出了不少基于非线性优化的训练算法。本文采用基于非线性最小二乘法的 LM 算法。
3、 遗传算法优化神经网络初始权值和阈值的实现
遗传算法(Genetic Algorithms) 是模拟生物学中“物竞天择、适者生存”的自然选择和基因遗传机制提出的并行随机优化算法。遗传算法优化神经网络初始权值和阈值的实现过程:
⑴基因编码。GA 工具箱支持二进制编码、格雷编码和浮点编码。本文采用浮点编码。
⑵产生初始种群。由于遗传算法的群体型操作需要,所以必须为遗传操作准备一个由若干初始解组成的初始群体。种群规模越大,搜索范围越大,越不易陷入局部极小,但搜索时间越长。本文初始群体取为 200。
⑶适应度评估检测。遗传算法在搜索进化过程中一般不需要其他外部信息,仅用适应度值来评估个体和解的优劣,并作为以后遗传操作的依据。适应度函数可直接取为目标函数也可以经目标函数转换得出。本文选择神经网络对第一组输入参数经过不同初始权值和阈值进行训练后的输出质量流量与理论输出质量流量的平方差的倒数作为适应度函数,即

其中 ObjV 为目标函数,T 为理论质量流量,A 为训练所得质量流量。
⑷选择。选择或复制操作是为了从当前群体中选出优良的个体,使他们有机会作为父代为下一代繁殖子孙。GA 工具箱支持轮盘赌选择和随机遍历抽样选择。本文采用轮盘赌选择。
⑸交叉。交叉操作是遗传算法中最主要的遗传操作。它仿照生物学的交配,将一对染色体按单点或多点进行交换重组从而产生新个体。本文采用单点交叉,交叉概率取为 0. 9。
⑹变异。变异操作是按位进行的,即把某一位的内容进行变异。变异操作同样也是随机进行的。对于浮点编码,具体操作是将随机数加到变异位得到变异之后的结果。一般而言,变异概率都比较小,变异操作需要和交叉操作配合使用,目的是挖掘群体中个体的多样性,克服可能出现的局部解弊病。一般变异概率取 0. 01 ~0. 2,本文对变异概率进行了自适应操作,对适应度大的个体取较小的变异概率,对适应度小的个体取较大的变异概率。
⑺终止搜索。遗传算法是一个反复迭代的过程,每次迭代都要计算适应度,进行选择、交叉、变异操作,产生子代,直至满足终止条件。本文制定的最大遗传代数为 100。
实现算法的流程如下图 2 所示。
4、 关联结果与讨论
没有经过遗传算法优化初始权值和阈值的神经网络关联式训练样本误差如表 3 所示,其中平均误差和最大误差分别定义为
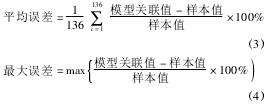
经过遗传算法优化之后的神经网络关联式训练样本的误差如表 4 所示。



从表 3 中可以看出,神经网络对于这四种制冷剂的关联效果相近,这表明神经网络四种制冷剂具有一定的适应性,并且平均关联误差与最大关联误差都足以满足工程精度的需要。从表 4 中可以看出,经过遗传算法优化后的神经网络关联模型的适用性没有被破坏。
对比表 3 与表 4 可知,遗传算法优化之后的神经网络模型提高了训练的精度以及训练的速度。对比制冷剂 R407C 优化前后的关联误差,优化前训练 325 次达到 0. 0216% 的平均误差的最大误差,而经过优化之后,只需要次便可以达到 0. 0173% 的平均误差,2. 3502% 的最大误差,关联精度提高了 19. 9%,关联速度提高了 41. 8%。优化之后对于 R134A 的关联速度提升效果明显,优化之前达到平均精度为需要训练 330 次,优化之后只需要训练次便可以使平均精度达到 0. 0176% 。
5、 结论
本文采用遗传算法对流量特性神经网络关联模型的初始权值与阈值进行了优化,通过与优化之前的流量特性关联的对比,结果表明用遗传算法优化神经网络关联模型的方法可以应用到毛细管流量特性关联中,并且可以提高模型的关联精度以及关联速度。





