摘 要: 热力学第二定律可以用来判断过程的可能性 (即方向性) 。但对于具体的过程, 判据其是否违反热力学第二定律并非易事。在热力学中, 人们通常是把热力学第二定律发展成特定体系的热力学判据。本文主要回顾总结了热力学第二定律的提出、表述形式、数学表达式及其在具体体系中的应用。
关键词: 热力学第二定律; 热力学判据; 熵; 亥姆霍兹自由能; 吉布斯自由能;
Abstract: The second law of thermodynamics can be used to judge if a process can occur.But it is not easy to determine whether the occurrence of a process breaks the second law of thermodynamics.In thermodynamics, the second law of thermodynamics is usually expressed as thermodynamic criterions for a particular system.This paper mainly reviews the formulation, expression form, mathematical expression and application of the second law of thermodynamics.
Keyword: the second law of thermodynamics; thermodynamic criterions; entropy; helmholtz free energy; gibbs free energy;
热力学第一定律和热力学第二定律是人类在长期实践过程中总结出来的自然界的普遍经验定律。热力学第一定律就是热力学中的能量守恒定律, 即系统发生一个过程, 其总能量是守恒的。然而, 遵守热力学第一定律的过程并不一定能发生。如何判断一个过程的方向, 则是热力学第二定律的主要任务。热力学第二定律是高等学校本科生《物理化学》课程中的重要内容之一, 也是同学们学习的难点。热力学第二定律虽然指出了过程的“可能性”, 但对于具体的过程, 要判断其是否违反热力学第二定律并非易事。因此, 在热力学中, 人们通常是把热力学第二定律表达成数学公式, 进而发展成特定体系的判据。本文主要回顾总结了热力学第二定律的提出、表述形式、数学表达式及其在具体体系中的应用。
一、热力学第二定律的提出
热力学第二定律是人们在研究自发过程的共同特征的基础上提出的。所谓的自发过程指的是无需外力帮助 (无非体积功) 系统自动发生的过程。人们在实践过程中发现一切自发过程都具有做功的本领, 而且一切自发过程都是不可逆的。当自发过程发生后, 要想使系统恢复到原来的始态, 环境总是得到热量而付出功。如果假设环境能够将得到的热全部转化为功, 而不发生其他变化, 那么环境也就复原了。但是人们经过大量的实验证明上述假设是不可能实现的。实践表明这主要是由于热功转换的不等价性所引起的。即, 功可以无代价地全部转换成热, 而热不可能无代价地全部转换为功。因此, 自发过程不可逆性的根本原因是热功转换的不等价性。人们通过总结大量自发过程的不可逆性, 提出了一个自然界的普遍规律, 即热力学第二定律。其有两个代表性的说法[1]: (1) 克劳修斯说法:热不可能由低温物体传到高温物体而不引起其他变化。 (2) 开尔文说法:不可能从单一热源取出热, 使其全部转变成功, 而不发生其他变化。上述热力学第二定律指出那些“不可能”发生的过程。
因此, 对于一个具体的过程, 我们如果要判断它能不能发生, 就是看这个过程发生后是否违反了上述的热力学第二定律。如果该过程的发生违反了热力学第二定律, 那它就是不可能发生的过程。但是, 把一个具体过程转化成上述热力学第二定律的问题来判断它可不可能发生并非易事。人们通常希望把热力学第二定律表达成一个浅显易懂的数学式子。

二、热力学第二定律的数学表达式
卡诺在热机方面的工作为热力学第二定律的数学表达奠定了基础。卡诺提出了着名的卡诺定理, 即:所用工作于同温热源与同温冷源之间的热机, 其效率不可能超过可逆机。克劳修斯利用卡诺循环中热温商之和等于零这一结论, 推导出任意可逆循环的热温商之和都等于零, 从而发现了熵函数的存在。熵函数具有状态函数的特点, 只和过程的始终态有关, 而和具体的途径无关。对于可逆过程来说, 熵变等于过程的热温商之和。进一步, 克劳修斯利用卡诺定理中的小于号, 亦即不可逆热机的效率小于可逆热机的效率, 推导出任意不可逆循环的热温商之和都小于零。对于不可逆过程, 克劳修斯发现其熵变大于过程的热温商之和。自然界中只存在可逆和不可逆两种过程, 因此, 封闭系统中不可能发生熵变小于热温商之和的过程。克劳修斯将封闭系统中热力学第二定律表达成如下数学表达式, 即克劳修斯不等式[2]。
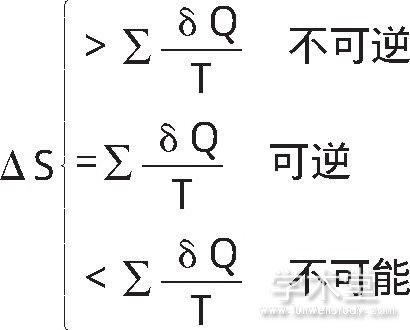
有了上述克劳修斯不等式之后, 判断封闭系统中一个过程能否发生就变得相对比较简单了。我们只需要计算过程的熵变ΔS和过程的热温商之和 , 通过比较它们之间的相对大小能够判断这个过程能否发生以及发生的过程是否可逆。如果将克劳修斯不等式应用于具体体系中, 我们就得到了热力学中的三个判据。
三、热力学判据
1. 熵判据:
如果把克劳修斯不等式应用到孤立系统中, 我们就得到了熵判据。孤立体系指的是系统与环境之间既没有物质交换, 也没有能量 (包括功和热) 交换。因此孤立体系中发生的过程热温商之和都为零。克劳修斯不等式表示如下。

即孤立体系中发生一个过程, 如果该过程的熵变大于零, 则该过程为不可逆过程。由于孤立体系中发生的过程不受环境的影响, 因此孤立体系中的不可逆过程一定是自发过程。如果该过程的熵变等于零, 则该过程是可逆过程, 亦即系统达到平衡。孤立体系中不可能发生熵减少的过程。综合上面这三种情况, 我们可以得到如下结论:孤立体系的熵永不减少。孤立体系中发生的过程, 总是朝着熵增加的方向进行, 直至体系的熵达到最大值。这就是孤立体系中的熵增加原理。但孤立体系是自然界中的一个极为特殊的体系, 上述熵判据并不具有普遍性。通常人们把体系和与体系相关的环境作为一个大的孤立体系。显然, 这个大的孤立体系必须服从熵增加原理。因此, 通过计算大孤立体系的熵变可以判断大孤立系统中的过程是否自发的。如果大孤立体系中的过程是自发 (或可逆) 的, 且没有非体积功, 那么体系中过程就是自发 (或可逆) 过程。在处理实际问题时, 系统可以作为孤立系统的情况并不常见。如果重新划定大孤立系统, 需要分别计算体系和环境熵变的计算。实际问题中常见的过程往往是等温等容或等温等压过程, 人们希望把克劳修斯不等式应用到这两种过程中来判断过程是否自发。
2. 亥姆霍兹自由能判据:
对于等温等容且无非体积功的过程, 体积功为零 (体积不变) , 非体积功也为零。克劳修斯不等式应用到这种特定的体系中之后, 我们就得到了亥姆霍兹自由能判据。

即在等温等容且无非体积功的条件下系统发生一个过程, 如果该过程的亥姆霍自由能降低, 则该过程为不可逆过程。由于无非体积功, 则不可逆过程一定是自发过程。如果亥姆霍自由能不变, 则该过程是可逆过程, 系统达到平衡。在该条件下, 不可能发生亥姆霍自由能增加的过程。亦即, 在等温等容且无非体积功的条件下, 封闭系统中发生的过程一定是朝着亥姆霍自由能降低的方向进行, 直至体系的亥姆霍自由能最低。
3. 吉布斯自由能判据:
等温等压且无非体积功的体系是实际过程中最常见的体系。大多学化学反应都是在等温等压且无非体积功的条件下进行的。寻找这种特定体系的判据更具实际意义。将克劳修斯不等式应用到等温等压且无非体积功的体系时, 我们就得到了吉布斯自由能判据。

即在等温等压且无非体积功的条件下系统发生一个过程, 如果该过程的吉布斯自由能降低, 则该过程为不可逆过程。由于无非体积功, 则不可逆过程一定是自发过程。如果吉布斯自由能不变, 则该过程是可逆过程, 系统达到平衡。在该条件下, 不可能发生吉布斯自由能增加的过程。亦即, 在等温等压且无非体积功的条件下, 封闭系统中发生的过程一定是朝着吉布斯自由能降低的方向进行, 直至体系的吉布斯自由能最低。
四、结论
本文能够使同学们明确热力学判据的发展过程及其适用的条件, 理解物理化学处理问题的思想, 即从实践上升到理论, 再用理论来指导具体实践, 增强同学们学习物理化学的信心。
参考文献:
[1]傅献彩, 沈文霞, 姚天扬, 侯文华.物理化学 (第五版) 上册[M].高等教育出版社, 2005.
[2] 朱文涛.基础物理化学 (第五版) 上册[M].清华大学出版社, 1995.





