
数学建模是将数学与实际问题联结的桥梁,是将数学知识转化为科学技术的重要途径。知识是有限的,创新是无限的,而数学建模就是培养创新的好载体。因此,培养大学生的数学建模能力,将数学建模的思想融入高等数学教学势在必行。
一、将数学建模思想与方法融入到高数教学中的必要性
(一)有助于培养学生学习高等数学的兴趣
将数学建模的思想与方法融入到教学中,改变传统的知识传授方式,可以加深学生对数学知识的理解、运用,体会到数学广泛的应用价值,调动学生的积极性,激发其学习兴趣。
(二)有助于培养和提高学生的自身能力
在高数教学中融入数学建模思想、方法有助于培养和提高学生以下几方面的能力:1.培养学生的创新意识和创新能力。2.培养和提高学生对数学知识、数学思想的综合应用能力。3.提高学生的实践能力。4.培养学生通过各种手段查阅、收集文献资料,主动学习的能力。5.提高学生对实际问题的观察力、创造力、逻辑思维能力并用数学语言对问题进行翻译、总结、表达的能力。6.培养学生利用计算机等科技手段解决问题的能力。7.培养学生与人沟通、协调的组织能力和团队协作精神。8.培养学生撰写论文的文字写作能力。
(三)有助于促进高等数学的教学改革
将数学建模思想和方法融入到高等数学教学之中是对数学教学体系的新尝试和革新,是传授高等数学知识的新思路、新途径,它将成为今后教学改革的主体方向,对高等数学的教学改革起到促进、推动作用。
(四)有助于提升教师自身素质和教学水平
在教学中融入数学建模思想和方法对教师自身素质要求更高,不仅要求教师对数学建模有充分的了解,要求教师对数学知识中建模思想和方法的体现有充分的认识,还要求教师将这种建模思想和方法体现在日常的教学中。这种教学方法要具有创造性,教师应充分发挥自身的主导作用和学生的主体作用,熟悉数学建模思想和方法的体现和建模的全过程,提高教学水平和效果,从而有助于提高自身的素质和教学团队的整体水平。
二、将数学建模思想与方法融入到高数教学中的途径
(一)在讲授数学定义、概念过程中融入数学建模思想和方法
高等数学的许多定义、概念都具有数学建模的特征,因此,可以借助实际背景,抽象出数学概念,培养学生的数学建模意识。例如:可通过引入变速直线运动的瞬时速度、过曲线上一点的切线斜率、成本变化率等数学模型来抽象出导数的概念f'(x)

的路程等问题建立模型,引出定积分的定义
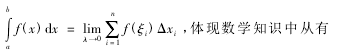
模型求解:由于纪念币价值每时每刻都在变化,当x趋于无穷大的时候可以将纪念币价值看做是在连续变化,所以当x趋于无穷大时,对函数U(x)求极限就可以得到经过K年后所具有的价值I,而

这样的应用型问题有很多,比如介绍极限应用的蛛网模型,介绍导数应用的最大利润问题,易拉罐尺寸的最优设计问题等,还有微分方程应用的减肥问题等。
(四)将数学建模思想和方法融入到考试命题中
为了将建模思想方法与教学相结合,我们可以在考试命题上做一些尝试,适当地将一些开放型的应用题设计入试题,要求学生用数学建模的方法解答,还可尝试改变传统考核方式,通过设计应用型问题并提交建模小论文,将考核成绩计入期末考核成绩,这不仅能考查学生的素质水平,还能提高学生的建模能力。
(五)将数学建模思想和方法融入到课后作业中
在课下安排一些利用数学建模思想和方法解决实际问题的内容,让学生利用所学知识进行分析、探讨,可以多名学生自由组队,利用所学知识,通过分工协作,在图书馆查阅书籍资料,利用网络、计算机、各种现代信息技术工具进行搜索,共同完成作业内容。在完成作业的过程中,能够培养学生团结合作、创新、知识应用等能力,锻炼学生的沟通能力、利用通讯工具进行资料收集的能力以及运用数学知识解决实际问题的能力。
参考文献:
[1]姜启源,谢金星。数学模型[M].北京:高等教育出版社,2003.
[2]何志树,叶殷。数学建模思想在教学中的渗透与实践初探[J].武汉科技学院学报,2005(11)。
[3]吕跃进。在高等数学教学中贯彻数学建模思想[J].广西高教研究,1994(3)。
[4]巨泽旺,孙忠民。浅谈高等数学教学中的数学建模思想[J].中国科技创新导刊,2009(17)。
[5]李传伟。数学建模的教学探讨[J].成都大学学报(教育科学版),2007(3)。





