
0、 引言
区域寻优过程的稳定数学模型分析对于许多实际的数学应用具有很好的指导意义。研究区域寻优过程可以大大提高许多优化解的解精度。首先构建寻优过程的稳定数学模型,在此基础上,使用较大的迭代步骤提高收敛速度,将解稳定的固定在区域后,使用小的迭代步骤逐步靠近优化解,大大提高解的精度。通过数学推导证明了区域寻优过程可以通过本文变步长迭代的方法收敛于最优解,从理论和实验上系统分析本文模型的可行性和变步长迭代过程的收敛性。
1、 寻优过程数学模型可行性和稳定性分析
1.1数学模型可行性分析
寻优过程模型的可行性分析需要满足以下条件:条件1:矩阵因子 aii大于0,可以作为运算的区域寻优分母应用;条件2:迭代向量 xj(k)的下一步迭代 xj(k+1)具有区域寻优可参性;条件3:xi(k)因子的迭代加速具有区域寻优收敛性。
(1)矩阵因子 aii代表区域寻优运算过程中矩阵 a的 i*i 量值,由于在区域寻优运算过程中,矩阵因子作为运算加权的值存在,其代表矩阵对角线上的元素,即xi2,所以是个非负数值,又因为在寻优运算过程中,元素 xi是一个非0值的数,所以 aii大于0,条件1得证。
(2) 区域寻优变步长迭代格式为:
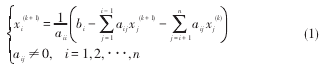
式中:xi(k+1)— i 向量第 k+1步区域寻优的迭代值;xj(k+1)— j 向量第 k+1步区域寻优的迭代值;xj(k)— j 向量第 k 步区域寻优的迭代值;aij—区域寻优加权系数;bi—区域寻优偏置值,一般为固定数。从上式的迭代步骤来看,在区域寻优迭代过程中,充分考虑了系统第 k 步和第 k+1步的实际情况,所以相邻两步之间的数据均得到了一定的加权使用,使得历史数据的作用得以生效,所以第 k 步和第 k+1步具有可参性。条件2得证。
综上分析,该区域寻优变步长迭代收敛的区域寻优数学模型分析具有很好的可行性,可以作为寻优过程的模型分析。
1.2变步长迭代数学模型稳定性分析
区域寻优变步长迭代数学模型的输入因子为:


所以该区域寻优变步长迭代数学模型对于不同的输入数据具有很好的冗余处理,即模型是稳定的。
2、 区域寻优变步长迭代寻优实现方法
区域寻优变步长迭代寻优算法,假设变步长迭代寻优过程中的真值模型与误差模型为:

经过区域寻优变步长迭代误差分离计算后,再引入改进固定点算法滤除误差,该算法需要对接收真值进行预处理,数学表达式为:
X'=X-E{ X}(20)
区域寻优进行变步长迭代分离是将误差与真值之间的关联性降为0,使得它们之间没有关联,以便于进行误差分离,同时也可以提高算法整体的计算速率,使得算法进行区域变步长迭代寻优时收敛更快,算法整体的稳定性也得到了相应的提高。其中:
E{[ X]}-E{ X }[ X]-E{ X}T=DΛDT(21)
采用真值特征值分解得到区域寻优变步长迭代分离真值:

式中 β 越大代表整个区域寻优变步长迭代函数越陡峭,区域寻优变步长迭代的收敛速度也就越快。当真值变步长迭代分离处理结束以后,将变步长迭代分离真值进行处理得到:

由此得到区域寻优变步长迭代寻优的运算步骤如下:
(1) 将真值进行区域寻优变步长迭代定位,得到一个相对范围较小的区域;(2) 通过区域寻优变步长迭代寻优算法对真值进行分解,去除误差影响;(3)将真值进行区域寻优变步长迭代分离;(4)最后当结果达到表达式时停止迭代。
3、 实验与结果分析
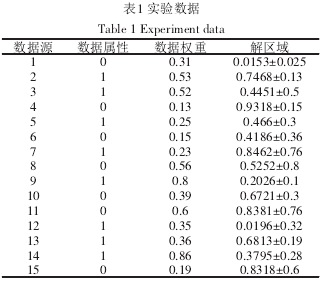
为了测试基于变步长迭代收敛的区域寻优方法建立的稳定数学模型对于实际求解数学模型的性能优劣,采用实际的数学应用数据进行分析测试,构建测试数据详细信息见表1。
区域寻优变步长迭代速度的比较曲线如图1所示。
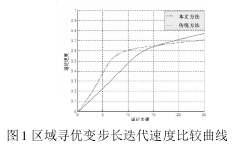
从图1可以看出,本文稳定模型下的改进方法的区域寻优变步长迭代速度高于传统非线性模型下的非线性步进寻优方法,平均提高了20%,具有更加优越的区域寻优变步长迭代效果。区域寻优稳定误差的比较曲线如图2所示。
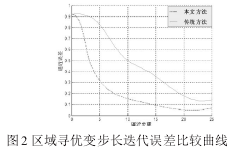
从图2可以看出,采用稳定模型下的改进方法的区域寻优变步长迭代误差远小于采用传统非线性模型下的非线性步进寻优方法的变步长迭代误差,平均迭代误差降低了35%。
4、 结论
研究了一种基于区域寻优变步长迭代寻优过程的稳定数学模型。经过数学理论论证和实际测试,该模型下的分析方法相对于传统的非线性模型下的非线性步进寻优方法,区域寻优变步长迭代速度平均提高了20%,区域寻优变步长迭代误差平均降低了35%,具有很强的实际应用前景。
参考文献:
[1] 赵登福,王蒙,张讲社,等.基于支持向量机方法的短期负荷预测[J].中国电机工程学报,2002,22(4):26-30.
[2] 顾 彬,郑关胜,王建东. 增量和减量式标准分类的分析[J]. 软件学报, 2013,1:1-13.
[3] 杨干山. 具有二阶变步长迭代效应场多维Landau-Lifshitz方程解的极限行为[J].中国科技.数学,2013,43(5):444-475.
[4] 顾春,石焕南. 反向Chrystal不等式[J]. 数学的实践与认识,2008, 33(13):17-19.
[5] 刘国祥. 构造函数证明平均不等式[J]. 赤峰学院学报(自然科学版),2009,25(8):5-6.
[6] 姜卫东. 关于 Seiffert 平均的一个不等式[J]. 大学数学,2009, 12(1):12-15.





