
随着科学技术特别是信息技术的高速发展,数学的应用价值越来越受到人们的重视。利用数学知识解决生活中的实际问题已成为当今数学界普遍关注的课题。
因此,学生只掌握书本知识已不能满足社会的需求。教师应引导学生把所学的数学知识与生活中的实际问题相结合,开展数学建模活动应成为数学教学的重要方法之一。所谓数学建模是用数学方法建立数学模型。数学模型是反映特定的具体实体的内在规律性的数学结构,它是从客观原型中抽象概括出来的完全形式化和符号化了的模型,它比原形简单,又高于原形。因此,利用数学建模解决数学问题,往往会收到事半功倍的效果,下面举例对其加以浅析。【图1】
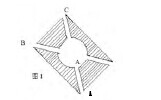
例1:(如图1),是一块长方形绿地,如果绿地长AB=40米,宽BC=20米,那么A、C两点间的距离是多少?
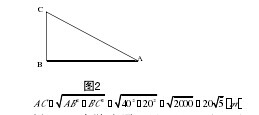
解析:要解决上述问题,只需以AB、BC为直角边,AC为斜边建立一个直角三角形数学模型(如图2所示),然后利用勾股定理进行计算。【图2】
例2:一个游戏题,甲、乙、丙、丁与小强五位同学一起比赛下象棋,到现在为止,甲赛了四盘,乙赛了三盘,丙赛了两盘,丁赛了一盘,小强赛了几盘?
解析:此题若建立数学模型,画出图形,答案将一目了然。
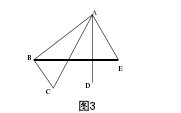
用点A、B、C、D、E分别表示甲、乙、丙、丁、小强,两人间的比赛用线段连接,那么根据题意,可建立如图3所示的数学模型,这样,小强赛了几盘的问题就转变成了从E点出发连了几条线段的问题。由图3可知,从E点出发的线段有两条,所以小强只赛了两盘。【图3】
例3:某校参加数学竞赛的学生中有120名男生、80名女生,参加英语竞赛的有120名女生、80名男生,已知该校共有260名学生参加了竞赛,其中有75名男生两科竞赛都参加了,那么参加了数学竞赛而没有参加英语竞赛的女生有多少人?
解析:这个问题的已知条件比较复杂,但倘若我们画出如图4所示的数学模型,用A、B两个圆分别表示参加数学竞赛的男、女生人数,C、D两个圆分别表示参加英语竞赛的男、女生人数,那么问题将迎刃而解。【图4】
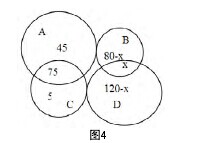
设 两 科 都 参 加 的 女 生 人 数 为 x ,那 么 只 参 加 数 学 竞 赛 的 男 生 人 数 是120-75=45,只参加英语竞赛的男生人数是80-75=5,只参加数学竞赛的女生人数是80-x,只参加英语竞赛的女生人数是120-x,则根据图4所示可得方程
(120-x)+(80-x)+x+45+75+5=260
解得x=65
故只参加数学竞赛的女生人数为80-x=15(人)。
例4:哥尼斯堡七桥问题
18世纪欧洲东普鲁士(现为苏联加里宁格勒)哥尼斯堡近郊有一条河,河中有两个岛,两岸与两岛之间架有七座桥(如图5)。当时城中居民热烈地讨论着这样一个问题:一个散步者怎样走才能不重复地走遍所有这七座桥并能回到原出发点?【图5】
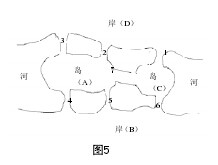
这个问题初看起来似乎不太难,但谁也找不出问题的答案,而以失败告终。当时大数学家欧拉从众人的失败中想到,这样的走法可能根本就不存在。随后他用数学模型的方法证实了自己的猜想是正确的,并于1736年表发了图论的第一篇论文《哥尼斯堡的七座桥》。欧拉的证明方法的思路是:
第一步,用符号A,C表示两个岛;B,D表示两个岸;1,2,3,4,5,6,7分别表示七座桥。
第二步,将两个岸和两个岛看成四个点,七座桥看成七条线。
经过以上数学抽象,哥尼斯堡七桥问题就转化成数学模型图6所示的“一笔画”问题。【图6】
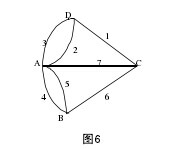
所谓“一笔画”是指能一笔画成的图形,需要满足以下三个条件:
(1)下笔后图形未完成前笔不能离开纸;
(2)每条线不能重复只能画一次;
(3)画时线条允许交叉。
欧拉进一步分析凡一笔画成的图形,如若起点和终点重合,则经过此点的线必是偶数条。然而图6是封闭的复连通域,而且经过A、B、C、D四个点的线条皆是奇数,所以图6不能一笔画成,因此,可断定哥尼斯堡七桥问题没有解。
综上所述,数学模型的建立,可使所解问题由难变易,由繁变简。巧妙地应用数学建模,不仅使解题变得简单,还能有效地培养学生抽象思维能力。在数学教学过程中渗透数学建模思想,可以让学生将其与数学方法相结合去解决实际问题,还可以使其对学习数学产生更大的兴趣。因此,教师在数学教学中,应适时渗透数学模型思想和方法,使学生能熟练地用其解决实际问题,以提高学生的数学素养。





