摘 要: 随着资源紧缺及污染问题的日益突出,目前在化工生产过程中通过节约原料、降低能耗及制造成本成为化工企业可持续发展的有效手段,通过在生产中科学合理的应用数学建模成为优化化工生产的一种有效方法,因此文章主要对数学建模方法应用于快捷设计化工生产中的实现路径进行了分析和研究,并以化工园区应急管理为例介绍数学建模方法的应用方案,通过模糊数学模型与层次分析方法的综合运用实现了对应急管理能力的系统评价和等级的综合评判过程,为优化和完善化工生产过程提供参考。
关键词: 数学建模; 化工生产过程; 设计方法; 模糊数学模型; 应急管理评价;
Abstract: With the shortage of resources and the increasing problem of pollution,currently in the chemical production process,saving raw materials,reducing energy consumption and manufacturing costs has become an effective means for the sustainable development of chemical companies,and scientific and reasonable application of mathematical modeling in production has become an effective method for optimizing chemical production,this paper mainly analyzes and studies the implementation path of mathematical modeling methods in the rapid design of chemical production,and takes the emergency management of chemical parks as an example to introduce the application of mathematical modeling methods,through the comprehensive application of fuzzy mathematical model and analytic hierarchy process, realizes the systematic evaluation and comprehensive evaluation process of emergency management capabilities,and provides a reference for optimizing and improving the chemical production process.
Keyword: mathematical modeling; chemical production process; design method; fuzzy mathematical model; emer-gency management evaluation;
0、 引言
化学工业在国民经济中起到重要作用,现代化科学技术的发展进步需以数学(工程技术的核心)作为支撑,数学广泛应用于生产实践中,目前不断更新发展的数学研究与教育在化工工业中的应用质量仍然有待提高,化工行业的可持续发展需依赖于数学的发展,为有效满足优化操作(尤其是实时优化要求)要求,快速发展完善的计算机技术为数学建模在化工生产中的应用(包括技术更新优化)提供了强大的支撑,化学工程与技术专业人员需做到对化工实践操作的熟练掌握,并能够在此基础上不断优化化工生产过程,这就需要了解并掌握相关数学建模方法和技术原理知识并将其深入应用到化工过程中。

1 、数学建模基础知识
化学工业规模随着化学工程的持续发展呈几何数级快速增长,化学工业受到能源、环境、质量等要素的影响迫切需要深化改革和持续创新,不断提升的工业化水平促使市场对不同种类化工产品的需求量不断增加,同时对化工产品的生产效率与质量提出了更高的要求,数学建模作为工程学的重要构成可用于描述现实世界中的诸多现象(通过使用偏微分方程完成),而涉及到大量的对流、扩散、反应(包括传热)过程、流体动力学等的化学工程对构建虚拟原型的需求不断提高。线性的PDE(一种包含未知函数的偏导数方程)采取科学合理的公式及处理方式(包括Fourier级数、分离变量、变换、叠加等)通常能够获取明确形式的解答,但应用于实际中的PDE大多为非线性,极大的增加了获取非线性PDE的解的难度,需结合运用数值近似求解;均为线性的Poisson和热方程易于完成解析解的推导过程,但在解决唯一性问题和寻求通解形式方面不足较为明显。尤其是对于大多属于非线性的化工方程,可通过发送求解域离散为大量有限单元方式的使用实现PDE解的获取,通过科学合理假设或简化处理并获取小区域的解时。全部解的获取意味着大量方程的产生与求解,这一运算过程可能涉及到多次的算数操作,需结合运用多元化的工具软件实现问题求解计算能力的获取,如基于PC的COMSOL Multi physics软件(主要用于求解PDE问题)。目前有限元方法在结构力学、化工、电磁等众多领域得以普遍应用,针对PDE求解问题通过使用基于有限元方法的求解技术已实现了大量问题的求解[1]。
2、 数学建模是化工过程的重要手段
1)在化学工艺研究与装备制造中,结合运用数学方法与计算机技术成为现代化化工发展的重要途径,不断提高的能源价格及环保要求为化工生产带来了较大的挑战,产品价格与质量面临着全球化的市场竞争,促使化工行业发生了巨大转变,为顺应节能高效的发展理念,最优化技术作为一种主要用于表述这些现状的工程方式,给化工厂的设计与操作流程的优化完善提供了技术支撑,更好的满足化工生产多元化限制条件,在提高生产效率的同时降低了成本。计算机集成制造(CIM)意在有效落实最优化操作条件(通过完善工艺流程、提高自动化水平实现),计算机的计算能力会不断提升(根据根据摩尔法则),使用最优化技术求解问题的复杂程度随之扩大,需运用包含优化改进技术的计算机软件。此外,随着近年来化工企业业务种类及规模的不断扩大,部分化工产品仍然存在供需不平衡的问题,大部分化工产品供大于求,促使精细化工与合同化工生产领域发展起来,化学原料药物市场面对日益激烈的市场竞争需培养独立的竞争性优势以获取更多有效订单,其本质在于合成工艺开发过程的完善与创新发展,而生产工艺长远突破性发展的实现需在现有工艺的基础上,结合运用性价比较高且安全稳定的原料及科学合理的数学建模使生产流程得到有效简化,提高某一环节的生产质量及回收率,寻求简单高效的物理及化学处理方式减少废弃物排放[1]。
2)在化工生产管理与新品研发中运用基于计算机网络技术的数学建模,以满足现代化工企业的发展需求,未来化工企业的一项竞争优势在于可顺应国际市场需求的良好的全球供应链管理能力(基于技术创造实现),在此基础上实现通用产品及一些特殊类型产品的生产,从而能够以全球多样化的客户需求为依据提供有针对性的个性化服务。并且能够快速掌握市场需求的变化情况,据此研发和优化生产工艺与化学产品(具备新的功能特性),如基于生物技术使用数学建模提高化工企业生产通用与特殊产品的质量和效率。同时要求化工院校数学教学能够有机结合化工专业、与时俱进,更好的在化工生产中应用数学建模。
3、 利用数学建模优化设计化工过程的方法
3.1、 仿真实际应用
针对生产原料配置的化工工程仿真,为寻求最优化配置实现生产原料与物质的合理分布(将氯净化剂采用臭氧代替),充分利用数学建模软件COMSOL-Multi physics的配置功能进行实验仿真测试,使用该数学建模软件完成计算实现生产金属棒效率的有效提高,针对化工工艺过程通过模拟计算进一步适度优化改进工艺实现加工速度的显着提高。并且仿真作为化工工程专业的重要课程之一在教学过程中起到辅助学生深入理解关键性知识与公式等的作用(利用模拟软件完成),以传递现场课程中的流体动力学计算为例,可采用数学建模仿真完成对课程概念及其公式的模拟与解释,调动学生的兴趣与积极性。引用PDE对化工反应工程进行仿真已取得了一定的实效,目前数学工具已成为化工工程师普遍使用的工具,并据此实现对化工系统、工艺流程便捷高效的设计与优化过程,帮助工程师掌握模型构建与验证方式,并扩展其想象力、激发其不断进行深层探索,为更多新技术的研发打下基础[2]。
3.2、 实例仿真模拟
建模软件COMSOL Multi physics具有构建数学模型简便的优势,采用数学模型对耦合自由与多孔介质流动(指固定床反应器中)进行考察时,此过程主要涉及到两种反应物、一种产物共3种气体,在固定的多孔介质催化床注射物质(通过主管道与注射管完成)反应完成后获取相应产物构成,具体模拟流程为:
1)先完成相应几何模型的构建,并对具备不同属性的区域进行定义,为有效缩减计算量,对于具备一定对称性的反应器(包括管结构和注射管)只需模拟其中的一半。
2)完成相应物理设定,根据所选用的COMSOL Multi physics软件的应用模式完成对各区域属性(包括材料属性)及边界条件的设置,不同应用模式的物理设定均可设定为常数或任意表达式,对于多孔床中的流体流动情况(位于自由流动区与多孔介质区)通过方程Navier Stokes和Brinkman的使用完成详细描述过程,不同物质质量传递的模拟采用流扩散方程完成[3]。
3)接下来在数学建模软件中进行网格(由大量三角形或其他形状构成)剖分,基于已定义的物理场生成相应的网络用于代表整体系统,根据实际需要选择COMSOL Multi physics软件的缺省网格(包括三角形单元、四边形、四/六面体、棱柱等)后可手动划分网络,以便将其应用到各种不同实例中,此外为确保网格的精确性与可靠性,还可简洁使用框架选择相应区域完成网格的精细优化。
4)选择和运行求解器,COMSOL Multi physics软件提供缺省、参数化线性或非线性、静/动态线性、特征值、瞬态、自适应等多类求解器,以瞬态求解器为例,在明确软件求解时间及生成解流程的基础上,按照顺序分别二次对Brinkman、Navier Stokes、对流与扩散方程的求解过程,必要时软件可同时计算全部方程以避免反应过程对气体密度产生影响。
5)最终结果处理和图形化展示,COMSOL数学建模软件除了常用的图片、图表信息模式还提供动画制作功能,能够采用动画形式对化工反应过程随时间产生的转变进行详细分析(包括检查流场分、反应物/产物浓度等的分布情况)[4]。
4、 基于模糊数学模型的化工园区应急管理评价
近年来迅速发展的化工园区内的化学品种类和数量不断增加,分布较为集中的危险源存在极大的安全风险隐患,这要求开展高效的化工园区风险评价工作以有效降低化工园区的安全风险,其中的一个重要单元即为应急管理评价,应急管理是安全管理和风险评价的重要环节,本文以某化工园区应急管理系统作为研究对象,基于现有研究成果与该园区的现场调研结果对各类突发事件进行全面考虑(包括事前、事中、事后),通过模糊数学模型和层次分析法的综合运用实现对应急管理水平系统的评价过程,最终实现应急管理水平等级的综合评判,并找出应急管理存在的不足和漏洞,为进一步改善应急管理水平提供参考。
4.1、 建立数学模型
将反映被评事物的模糊指标采用等级模糊子集进行处理即为模糊综合评价,在此基础对各指标根据模糊变换原理完成模糊综合评价(即由低到高、逐层向上进行综合评价)获取目标层的评价结果,同时需二次综合评价准则层和目标层,基本步骤为:先完成由A={A1,A2,...Ai}(Ai={Ai1,Ai2,...Aij})表示的评价指标集的建立,然后完成权重集(Ai受各指标的影响程度)的确定,由Bi={Wi1,Wi2,...Wij}表示权重分配,由D={W1,W2,...Wi}表示Ai对A的权重集,以此类推;接下来以评价对象的特点为依据选择评语集建立评价等级(由适合的评语组成,即V={V1,V2,...VK}),建立指标评价矩阵R,指标Ai所属等级采用专家法完成判断,再对各指标隶属于V各等级的频数进行统计,各指标的隶属度为各频数同专家总数比例,Ai=Bi Ri和Ai={C1,C2,...Cj}对应各子目标的综合评价向量与评价矩阵,A=DB对应各总目标评价向量,最终完成应急管理水平等级的确定(以最大隶属度原则为依据)[5]。
4.2、 应急管理能力体系的构建
1)以化工园区的特点为依据确定应急管理评价指标体系,这是化工园区应急管理评价的基础和关键,应急管理属于一个多层次复杂系统,涉及到多种因素,本文从事前、事中、事后全过程出发考虑各类突发事件,将应急管理能力分为应急管理水平、一级评价指标(主要包含5个子系统)、二级评价指标(包含19个子系统)3个层次,具体如表1所示[6]。
表1 化工园区应急管理评价指标

2)各指标的权重分配,风险防控与应急准备是应急管理的关键所在,风险防控在应急管理中的重点在于风险控制,主要包括应急准备(主要针对应急预案、演练)、应急响应和恢复(以消防和善后处理为主)、资源保障(主要针对物质保障和应急平台),以各指标在应急管理中的作用为依据确定指标体系的权重集,其中,一级评价指标的权重表示如下:
二级评价指标的风险防控、应急准备、应急响应、应急恢复、资源保障的权重如下[7]。
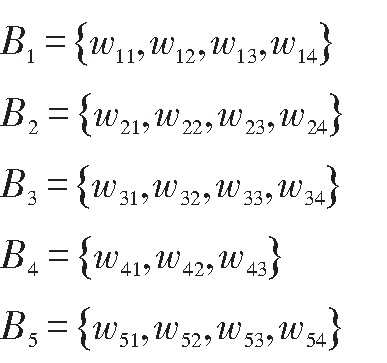
3)构建模糊函数关系,一级模糊综合评价:通过专家打分获取由Ri{i=1,2,...,i}表示的一级要素的评判矩阵,根据Ai=Bi·Rj完成模糊矩阵运算;二级模糊综合评价得到由R=(A1,A2,...Ai)表示的二级评判矩阵,在同第一层权重进行模糊矩阵运算,获取评价值:A=D·R,据此判断应急管理能力的等级。
4)评语等级的确定,本文采用分值法对各因素进行打分,以获取应急能力评价结果,评语等级如表2所示[8]。
表2 评语及等级说明

5 、结语
将数学建模应用到化工生产过程中可有效实现对生产工艺与原型等方面的优化改善,化工工艺的具体工作原理通常易于掌握和理解,但明确包括物料用量与配比、反应器种类与尺寸、最佳流速及反应条件等在内的最佳参数时涉及到的工作量较大,传统模式下通常需通过多次实验后以实际经验为依据实现相关问题的切实解决,该方法因涉及到大量原型装置的构建和测试工作而显着增加了使用成本。通过具备独特优势的数学建模工具的使用可完成相应虚拟原型(实时修正任意参数)科学合理的构建过程,进而更加直观实时的展示出化工工艺的内部机制,效果显着。
参考文献
[1]李江洪.高职高等数学教学改革与实践探索——以石油化工生产技术专业为例[J].科技资讯,2018(34):173-174.
[2]刘志平.基于数学建模和LabVIEW的虚拟仪表设计和研究[J].自动化与仪器仪表,2018(11):151-154.
[3]王美晨,李嘉萱,席典兵,等.基于数学建模下的CT图形成像及系统参数标定[J].电子制作,2018(13):49-53.
[4]马书红.基于煤化工的多能耦合系统全寿命周期经济评估数学模型构建[J].粘接,2019(06):132-135.
[5]周乃磊,王中琪,徐旭东.建立数学模型分析UVFenton对金属切削液废水的降解[J].环境工程学报,2018(07):2271-2275.
[6]辛禾,鞠立伟,李秋燕,等.计及资源互补特性的风光水储耦合系统运行策略及求解算法[J].可再生能源,2018(12):1833-1841.
[7]尤媛,李洪波,夏春雨,等.贾生晖.冷轧毛化工作辊表面粗糙度衰减过程的试验与数学模型研究[J].机械工程学报,2018(12):173-183.
[8]任贵红,张苗,谢飞,等.基于模糊数学和灰色关联分析的化工储罐区火灾风险评估研究[J].中国安全生产科学技术,2018(02):105-111.





