
引 言
兵棋(Wargame)是使用代表战场及军事力量的棋盘和棋子,依据从战争经验中总结的规则,并结合概率原理,通过推演各方人员的一系列决策对抗,对作战过程进行逻辑推演研究和评估的军事科学工具,是作战模拟的一种方法和手段。兵棋的发展经历了从手工兵棋到计算机兵棋系统的过程,特别是军事运筹学等理论的引入,使得兵棋发生了巨大变化。但无论在哪个阶段,兵棋以推演者为中心的本质特征没有改变,这也正是兵棋能够区别于其他类型的模型与模拟的根本原因。
兵棋通常包括三个基本要素:棋盘、棋子和规则。兵棋棋盘也称为兵棋地图(Wargame Map),是对兵棋推演的战场环境的模拟,手工兵棋和计算机兵棋中兵棋棋盘的作用有所不同。手工兵棋中的兵棋棋盘既要为推演者提供战场环境信息,使其达到认知战场环境的目的,又要推演者依据规则进行各种裁决提供环境数据支持,即实现了战场环境感知仿真和数据仿真的统一,而六角格网兵棋棋盘正是其典型样式。计算机兵棋中的兵棋棋盘(也可称为战场环境模型,主要指地形环境),其主要作用是为作战模型提供数据支撑并与之交互,更多体现了战场环境数据仿真的作用,因此,计算机兵棋还需要以电子地图、扫描地图或影像地图等多种方式为推演者提供战场环境信息,以使其实现对战场环境的认知。
由于计算机兵棋中作战单元等通常以经纬度描述其地理位置,兵棋棋盘则以地图格网编码描述位置信息,同时计算机兵棋系统还可能使用其他坐标系以辅助推演者进行快速定位,推演过程中必然涉及到地理坐标、兵棋棋盘格网编码及其他坐标系之间的坐标转换,因此,兵棋棋盘中坐标的快速转换对于兵棋推演效率而言具有重要意义。本文分析了基于Lambert等角割圆锥投影的计算机兵棋棋盘中经纬度坐标与六角格网编码的直接转换方法,并引入了过渡坐标系,提出了间接转换方法,详述了基本原理和转换公式,并通过实验对其转换效率进行验证。
1 直接坐标转换方法
由于Lambert等角割圆锥投影能够在较大区域范围内很好地保持方位关系,因此常被用于计算机兵棋系统中六角格网地形建模。
建模过程中,通常需要根据作战区域,选定两条标准纬线和一条中央经线,并据此确定各项投影参数。Lambert等角割圆锥投影示意图如图1所示。
根据六角格网的几何特性,利用Lambert等角割圆锥投影得到的直角坐标系统,可以在横向和纵向上分别进行等间隔的划分,并据此建立起矩形格网与六角格网的对应关系。直角坐标系等间隔划分原理如图2所示。图2中,点(minX,minY)为直角坐标系中作战区域的左下角点(西南角点),点(maxX, maxY)为直角坐标系中作战区域的右上角点(东北角点),点O为直角坐标系的原点,X_Dis为X方向上间隔距离,Y_Dis为Y方向上的间隔距离。
据此,可以得到经纬度坐标与六角格网代码之间的转换方法,其相互转换流程如图3所示。经纬度坐标与平面直角坐标的相互转换可以通过Lambert等角割圆锥正投影算法和逆投影算法实现。由平面直角坐标到六角格网编码的转换公式如式(1)所示。【1-2】

上述两式中,i,j分别为六角格网的横、纵编码,Lx,Ly分别为直角坐标系中横、纵坐标。
2 间接坐标转换方法
间接坐标转换方法的基本思路是引入新的六角格网编码系统,利用特定的算法建立新六角格网编码系统与经纬度坐标系和计算机兵棋系统中六角格网编码系统的坐标对应关系,并将其中部分转换参数预先计算以提高转换效率。图4描述了利用新六角格网编码系统进行坐标转换过程中,四种坐标系的相互转换基本流程,其中,(A)为地理坐标系,(B)为Lambert投影平面直角坐标系,(C)为新六角格编码坐标系,(D)为兵棋六角格网编码坐标系。图5描述了间接坐标转换法的基本几何原理。图5中,点O为Lambert等角割圆锥投影的同心圆心,点A,B,C,D分别为推演区域的西北、西南、东南和东北角点,F1和F2分别为地理坐标到Lambert平面直角坐标的投影半径和投影角。根据选定的标准纬线和中央经线,可以计算出坐标转换的相关参数。Lambert投影变换过程所用的参数可以通过式(3)计算得到。【3】

式中, 分别为标准纬线1和标准纬线2的弧度值。由Lambert投影变换公式可计算得到F1和F2的值,如式(4)所示。【4】

式中,lat,lon为待转换的经纬度坐标,CEN_LON为中央经线。间接坐标转换法将平面推演区域按照一定间隔等分为若干份,并根据推演区域范围和间隔长度计算得到平面矩形格网到新六角格编码系统的相关转换参数Fv1,Fv2。结合Fv1,Fv2,使用式(5)可以得到新六角格网编码系统中的位置坐标[i,j]。【5】

式中,LY2是推演区域的北部边界的Latnbert投影平而直角纵坐标。
至此,可以根据图吐中所小的新六角格网编码方式与兵棋六角格编码方式的关系,利用式(6)计算得到输入的经纬度坐标对应的兵棋六角格编网码系统中的格元编码。Lambert投影平面直角纵坐标。
至此,可以根据图4中所示的新六角格网编码方式与兵棋六角格编码方式的关系,利用式(6)计算得到输入的经纬度坐标对应的兵棋六角格编网码系统中的格元编码。【6】
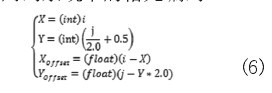
式中, 和 分别为当前位置相对于所在格元的中心点的横向、纵向偏移量。
3 实验结果及分析
对于计算机兵棋系统而言,由于存在多种坐标系,在作战模型与六角格网地形模型交互的过程中,必然涉及到经纬度坐标与六角格网编码之间的相互转换,同时兵棋推演过程中存在大量的交互过程,因此经纬度坐标与六角格网编码的相互转换效率将会对兵棋推演效率产生重要影响。
本文针对直接坐标转换方法和间接坐标转换方法,从经纬度坐标与六角格网编码正向和逆向转换方面,对两种方法进行试验。实验所用计算机配置为:处理器IntelCore i7-2720QM 2.20GHz、内存2.89GB。 本文利用直接坐标转换方法进行了10组试验,每组试验选取了10 000 000个经纬度坐标和六角格网编码进行正向和逆向转换。表1描述了直接坐标转换方法的正向和逆向转换试验结果,图6 (a)描述了10组正向坐标转换所用时间,图6 (b)描述了10组逆向坐标转换所用时间。 表2描述了使用间接坐标转换方法对10组坐标进行正向和逆向转换试验结果。
从实验结果可以看出,间接坐标转换法能够将经纬度坐标到六角格网编码的正向转换效率提高近3倍,逆向转换效率提高约20%,这对于提高计算机兵棋推演效率而言,具有十分重要的意义。
4 结束语
计算机兵棋系统具有计算快速、数据统计精准等特征,在推演过程中能够模拟大量的作战要素和作战环境要素,并能够对作战要素之间及作战要素与环境要素之间的交勺_关系进行有效的模拟。推演过程中通常要使用多种坐标系统,以完成模型交勺_、环境感知、态势报告等多种操作,而地理坐标系和六角格网坐标系是最为常用的坐标系统,因此,两种坐标系之间的坐标快速转换对于提高兵棋推演效率具有十分重要的意义。
本文分析了基于Lambert等角割圆锥投影的直接法坐标转换的基本原理,并提出了间接法实现经纬度坐标与六角格网编码的快速转换,实验结果证实间接法具有很高的正向和逆向坐标转换效率,能够为提高兵棋推演效率提供有力支撑。





