
镁合金作为一种结构材料,由于其密度低、比强度高、可以循环利用等诸多优点,而被广泛应用于航空航天等领域.在钢铁资源日益匮乏的今天,镁由于其物产丰富,被视为21世纪最具潜力的新型结构材料.
但是镁合金在其实际应用中也有一些缺陷,比如易氧化、不耐腐蚀等.为了使得镁合金的应用更加广泛,广大的科研者们都致力于新型高性能镁合金的研发,以解决现在镁合金在应用中遇到的瓶颈.
通过大量的实验发现,稀土元素添加到镁合金中可以在很大程度上改善其合金性能,而铈(Ce)元素作为应用最广的一种稀土元素,当其添加到镁合金中,由于在晶界附近有高熔点的Mg-Ce金属间化合物的形成,从而抑制了晶界滑移,提高了镁合金的高温抗蠕变能力.
在Mg-Ce金属间化合物中,Mg3Ce是其中最重要的一个相,在Mg-Ce合金微观结构的优化和力学性能的改善中扮演了重要的角色.Mg3Ce还是一个非常重要的镁基储氢材料.Ce元素具有磁性,而磁性对材料的性能有极大的影响.
由于以上的原因,Mg3Ce引起了广大科研工作者的关注和研究.
目前关于Mg3Ce的研究主要集中在其储氢性能、力学性能、化合物的合成等,但是在考虑Ce的磁性情况下,对Mg3Ce结构的理论研究还有欠缺,于是本文从这一点出发开始研究.在本文中,通过基于密度泛函理论的第一性原理计算,对Mg3Ce的磁性结构进行了研究.
首先在GGA计算下,对四种磁序结构:无磁性结构、铁磁结构、反铁磁结构第一类和第二类的稳定性进行了研究,由于计算结果与实验值不符合,因此引入了GGA+U的计算,通过Ueff的改变,发现当Ueff=7.0eV时,得到的结论和实验值很好地吻合.
最后,对Mg3Ce的电子结构做了进一步的研究,以便更进一步了解其内部机制.
1 计算方法
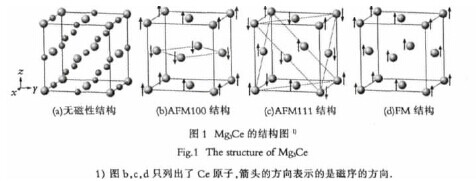
在本文中,所有的工作都是基于密度泛函理论(DFT)和平面波赝势的第一性原理计算软件Viennaab initio simulation package(VASP)来完成的.在本工作中,最外层的价电子和内层的电子之间的相互作用力采用缀加平面波方法(PAW)来替代描述,并且用广义梯度近似Perdew-Wang(GGA-PW91)版本来处理电子交换关联函数.平面波截断能选为350eV,在计算过程中,用1×1×1的晶胞,共16个原子,对于布里渊区K点网格数,选用的是9×9×9.计算模型如图1(a)所示,对于原子的弛豫,采用了共轭梯度(Conjugate-Gradient)算法,从而确保了体系总能变化的范围在10-4eV/atom内,我们认为体系达到优化条件,还需要限定未被束缚的原子上的Hellman-Feyman力不能大于0.01eV/?。【图1】
在计算电荷密度时K点的选取为11×11×11.对于含有磁性的Ce原子,为了更精确地描述电子间的强关联作用,在VASP计算中引入了Du-darev提出的DFT+U方法.具体在VASP中有两个参数U和J,它们分别代表的是库仑间的相互作用能与交换关联能,但是只有Ueff=U-J的值才是有意义的,在本文的计算中,我们一直保持J=1.0eV,对于DFT+U计算的更多参数设置如表1所示.【表1】

关于DFT+U计算方法的描述可以参考文献.
在本文中,对于Ueff的确定主要有以下两个因素:(1)Mg3Ce的基态结构应该是反铁磁第一类结构(即AFM100);(2)Mg3Ce的磁矩值.
对于含有磁性的原子,在计算中要分别考虑该种原子在无磁矩、磁矩为铁磁结构和磁矩为反铁磁结构三种基本情况.无磁矩的结构在计算时选用无自旋;对于反铁磁结构的计算选用自旋,另外,含有磁性的原子的初始磁矩设为一样的值;反铁磁结构的计算也是自旋情况下,含有磁性的原子在不同的原子面上的初始磁矩设为绝对值相等,互为正负的两个值.
2 结果与讨论
2.1 结构常数与稳定性
Mg3Ce具有以下的性质:在室温下的结构表现为BiF3类型,其空间群为FM-3M.在室温的情况下表现有近藤效应(含有极少量磁性杂质的晶态金属在低温下出现电阻极小的现象).Mg3Ce的Neel温度大约是4.1K,在Neel温度以下的时候,其磁序结构表现为反铁磁结构.在低温情况T=2K时,每个Ce原子的磁矩为0.59±0.04μB[29].
其晶格常数在温度为20K的时候为7.378(17)?,在室温的情况下,通过X射线衍射仪测得的晶格常数为7.444(15)?。Mg3Ce的全部信息如表2所示。【表2】
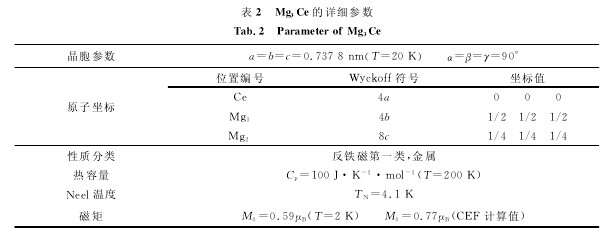
通过上述参数的结构优化之后,原子坐标与上述表格的位置相符合,并且我们计算得到的晶格常数为7.370?,与实验值和其他的理论计算值很接近,这一点说明了我们的计算参数是非常合理的.
2.2 基态结构的研究
如图1(a)所示,由于Mg3Ce中的Ce原子是面心立方结构,通过查阅文献,我们可以得知Mg3Ce可能存在的反铁磁结构有两种:反铁磁类型1(AFM100)和反铁磁类型2(AFM111).其磁序结构图如图1所示,其中箭头的方向表示磁矩的方向.为了确定Mg3Ce的基态结构,我们对图1所示的四种可能的磁序结构进行了计算研究,得到了在不同的晶格常数情况下的体系的总能关系曲线图,如图2所示.【图2】
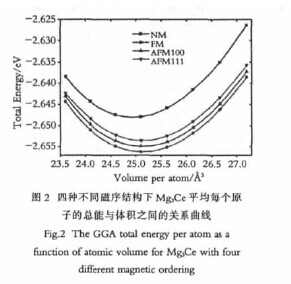
从图中我们可以看出,曲线的能量最低点时晶格常数为7.378?,这个与理论和实验值比较符合.对于四种磁序结构,其总能的排序是:能量最低的是铁磁结构,然后依次是反铁磁第一类、反铁磁第二类,能量最高的是无磁结构.其中前三者之间的能量差比较小,而无磁结构的能量是远大于另外三种有磁机构的.所以对于Mg3Ce结构来说,磁性是一个很重要的参数,对体系有很重大的影响,则在其性质计算的时候一定要考虑到其磁性.
在GGA赝势下,其确定的基态结构是铁磁结构,这一点和实验值不符合(基态结构应该是反铁磁第一类),另外我们计算所得到的磁矩值为0.94μB,此值也和实验值与其他的理论计算值有很大的差距,所以GGA计算不能够很好地预测Mg3Ce的一些性质.
为了更为精确地确定Mg3Ce的基态结构,一定要考虑Ce原子4f态电子的关联作用的影响,因此,我们进行了GGA+U的计算.在GGA+U的计算中,最为重要的就是参数Ueff的确定,首先我们选取了反铁磁第一类和铁磁两种结构,分别计算了它们在不同的Ueff值情况下总能差值的变化情况,得到的结果如图3所示.【图3】
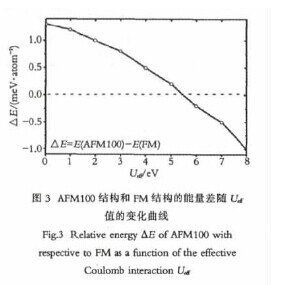
从图3可以看出,随着Ueff值的增加,AFM100和FM两种结构之间的总能差值变小,当Ueff大概在5.3eV的时候,两者的总能差值为零,当Ueff>5.3eV时,可以看出基态结构由FM逐渐转变为AFM100结构.
由于确定Ueff的因数有两个,一个就是前面说的基态的结构类型,第二个是Mg3Ce的磁矩值.
因此接下来我们研究了Mg3Ce的磁矩值与Ueff之间的关系,得到的关系曲线如图4所示.在图4中,将理论计算值与Ueff之间的关系曲线,实验值与温度之间的关系曲线共同展示.【图4】
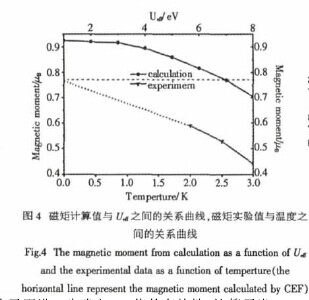
对于理论计算值,随着Ueff值的增加,其磁矩的值逐渐减少,并且当Ueff=7.0eV时,磁矩值为0.77μB,这个值和CEF的计算值很接近.
另外,对于实验值,通过查阅文献得到三个实验值(分别是2K,2.5K和3K),通过这三个值的外推,得到了在试验情况下0K时的磁矩值,如图4中的虚线所示,此外推值和理论计算值比较符合,所以我们认为Ueff=7.0eV在GGA+U计算中是比较合理的.为了更进一步确定Ueff值的有效性,计算了当Ueff=7.0eV时四种磁序结构平均每个原子的总能与平均每个原子的体积之间的关系,得到的曲线如图5所示.【图5】
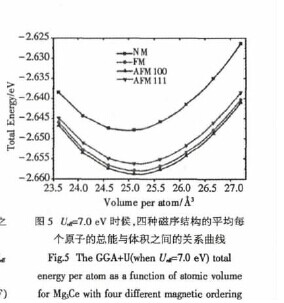
从图5可以看出,在Ueff=7.0eV时,其总能的最低结构是AFM100,并且其晶格常数也是7.378?,这些都和实验值很好地符合,另外对于磁矩值,由上面的计算值可以看出,也比较好地符合了实验值,所以我们认为Ueff=7.0eV在GGA+U计算中是合理的.
2.3 电子结构研究
为了更进一步研究Mg3Ce结构的内在机制,分别对它们的电子结构进行了研究.另外,到目前为止很少有研究关注稀土镁合金的稀土元素的f态电子,而在本文中,对Ce元素的f态电子也进行了研究.Mg3Ce晶体的态密度图如图6所示.
从图6(a)中可以看出Ce的f态电子和d态电子对总的态密度在费米能级附近的贡献很大,对于f态电子的上自旋的部分被电子态占据,而对于下自旋基本上都是空的,没有电子态占据.【图6】
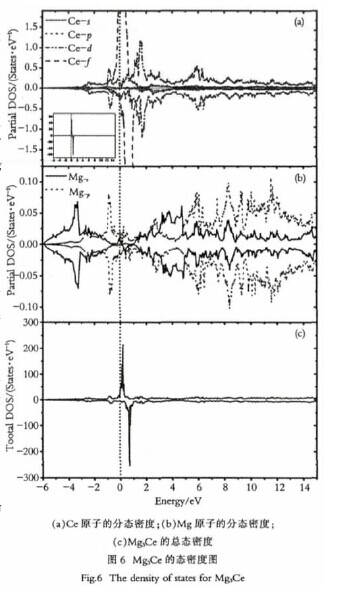
然而d态电子,只有一少部分被电子态占据,并且上下自旋部分相等,其余的大部分态都是空的.Ce的f态电子和d态电子明显的杂化更进一步地减少了Mg的价电子在费米能级附近的贡献,如图6(b)所示.
而且,在费米能级附近Mg的3p电子态要强于Mg的3s态电子,然而在离费米能级比较远的地方,Mg的3s态电子要比Mg的3p电 子 态 要 强.
从 图6(c)可 以 知 道Mg3Ce的总态密度主要是由Ce原子的4f态和5d态电子贡献,同样的还有Mg的3s态电子和Mg的3p态电子.其中4f电子态的贡献是不可以忽略的,因此对于Mg3Ce性能的研究必须要考虑到f态电子的贡献.
3 结论
采用基于密度泛函理论的第一性原理计算方法研究了Mg3Ce在GGA与GGA+U计算下的基态结构,计算结果显示:
(1)通过总能的计算,发现在GGA计算下,晶格常数为7.378?,与实验比较好地吻合,但是基态结构为FM(反铁磁结构),磁矩为0.94μB,这些都与实验值不符合,所以GGA计算不能很好地预测Mg3Ce的性质.
(2)由于GGA计算不能很好地预测Mg3Ce的性质,于是进行了GGA+U计算.通过基态结构和磁矩共同决定当Ueff=7.0eV的时候,GGA+U计算能很好预测Mg3Ce的性质.
(3)通过电子结构,进一步揭示了点缺陷结构和Mg3Ce的内在机制.发现Ce的f态电子对总的态密度的贡献是很大的,因此对于Mg3Ce性能的研究必须要考虑到f态电子的贡献.
参考文献
[1]YANG Z,LI J P,ZHANG J X,et al.Review on research and development of magnesium alloys[J].Acta Metallurgica Sinica(English Letters),2008,21(5):313-328.
[2]GANESHAN S,SHANG S L,WANG Y,et al.Effect of alloying elements on the elastic properties of Mg from first-principles cal-culations[J].Acta Mater,2009,57(13):3 876-3 884.
[3]AVEDESIAN M M,BAKER H S.Magnesium and magnesium alloys[M].New York:ASM International,1999.
[4]BECKER J,FISCHER G.Manufacturing and potential of extruded and forged magnesium products[M]//Magnesium-Alloys andTechnology.Weinheim:Wiley-VCH Verlag GmbH & Co.KGaA,2004:90-105.
[5]KAINER K U,VON BUCH F.The current state of technology and potential for further development of magnesium applications[M]//KAINER K U.Magnesium-Alloys and Technology.Weinheim:Wiley-VCH Verlag GmbH & Co.KGaA,2004:1-22.
[6]MORDIKE B L,EBERT T.Magnesium:Properties-applications-potential[J].Materials Science and Engineering:A,2001,302(1):37-45.
[7]PEKGULERYUZ M O,KAYA A A.Creep resistant magnesium alloys for Powertrain Applications[J].Adv Eng Mater,2003,5(12):866-878.
[8]ROKHLIN L L.Structure and properties of alloys of the Mg-REM system[J].Met Sci Heat Treat,2006,48(11-12):487-490.
[9]MORDIKE B L.Development of highly creep resistant magnesium alloys[J].J Mater Process Technol,2001,117(3):391-394.





