c语言论文第六篇:C语言学习过程中几种常用的算法
摘要:C语言是一门结构化的程序设计语言, 在解决实际问题时, 除了掌握扎实的基本语法知识, 更重要的是要学习如何编写程序。本文针对C语言程序设计课程实践教学中存在的问题, 从算法设计的角度, 对常用的递归算法, 排序算法, 迭代法, “打擂台”法, 辗转相除法等进行描述和分析。设计程序不仅保证算法的正确性, 还要考虑算法的质量。所以如何编写高效且正确的程序是至关重要的。
关键词:C语言; 算法; 程序设计;
著名计算机科学家Wirth提出“算法+数据结构=程序”。这一公式对于结构化设计语言是适用的[1]。算法是解决“做什么”和“怎么做”的问题, 数据结构是加工对象。所以不了解算法就谈不上程序设计。随着教学内容的增加, 程序设计的难度随之增大, 对特定问题设计相应的算法尤为重要。利用C语言的知识在解决实际问题时, 除了考虑算法和数据结构外, 还应采用结构化程序设计的方法进行程序设计。
C语言程序设计作为大学生的一门基础必修课程, 对提升大学生计算机编程能力至关重要, 也是后续专业课程学习的先修课程。在C语言教学过程中, 学生对程序设计往往显得力不从心, 特别是在程序设计实验课上, 对于一道程序难度不大的编程题, 部分学生却不知道如何下手去做。在教学过程中, 于清[2]建议以算法优先并结合案例教学的模式开展C语言的教学。屈婉玲[3]对算法课程的教学改革进行的总结。其他学者对C语言设计的递归算法[4,5]、排序算法[6]等分别进行了研究。
结合个人的实际教学情况, 本文对常见的几种算法进行分析。
1 算法与分析
该课程教学中, 涉及的典型算法有递归算法, 排序算法, 迭代法, “打擂台算法”, 辗转相除法等。
1.1 递归算法
递归的概念是, 在调用一个函数的过程中, 直接或间接调用该函数本身。递归算法的执行过程分为回溯和递推两个阶段[1]。在第一个回溯阶段, 把较复杂的问题求解到比原问题简单的一些问题。这个阶段, 必须要有结束递归的条件。在第二个递推的阶段, 当获得最简单情况的解后, 逐级返回, 依次得到稍复杂的解。
递归调用方式有直接递归调用和间接递归调用。常见应用于求解斐波那契数列[7]、汉诺塔问题[8,9]、树的遍历[10,11]、求阶乘 (见示例1) 等。
递归一般可以代替循环语句使用, 虽然程序结构优美, 但执行效率较低, 耗费计算机内存资源, 难以阅读和维护[12]。当效率处在第一位的时候, 还须谨慎使用递归。
示例1:求阶乘
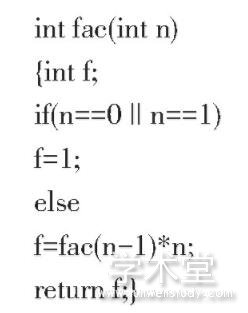
1.2 排序算法
排序方法按照排序的规律可分为“升序”和“降序”。排序的方法[13,14,15]有很多, 如希尔排序、堆排序、快速排序、冒泡排序、选择法排序等。在C语言课程教学中, 主要介绍的是冒泡法排序和简单选择法排序两种。
冒泡法升序排列若干个数的基本思想:每次将相邻两个数比较, 将小的调在前头。排序算法如下 (示例2所示) :
S1:比较第一个数与第二个数, 若前者大于后者, 则交换;然后比较第二个数与第三个数;依次类推, 直至第n-1个数和第n个数比较为止, 结果最大的数被安置在最后一个元素位置上;
S2:对前n-1个数进行第二趟冒泡排序, 结果使次大的数被安置在第n-1个元素位置;
S3:重复上述过程, 共经过n-1趟冒泡排序后, 排序结束。
示例2:对n个数使用冒泡法排序 (升序)
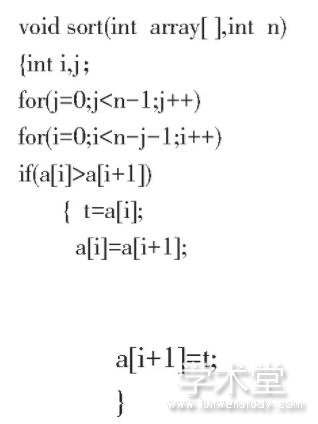
简单选择法排序的思想是:先将n个待排序中的最小数与第一个数对换;再将剩余n-1个数中的最小数与第二个数交换;如此往复, 找出一个未经排序的数中最小的一个。共比较n-1轮结束。示例3所示:
示例3:对n个数使用选择法排序 (升序)

冒泡法排序的效率不及快速排序和堆排序, 花费大量的时间, 但编写容易且稳定性高, 可应用在规模较小的排序算法中。简单选择法排序所需移动记录的次数较少, 稳定性好, 算法速度慢。
1.3 迭代算法
迭代法[16,17]是求解方程或方程近似根的一种常用的算法设计方法。例如用迭代法求, 求平方根的迭代公式 (示例4) :

S1:设定一个x的初值x0;
S2:用上述公式求出x的下一个值x1;
S3:再将x1代入以上公式右侧的xn, 求出x的下一个值x2;
S4:重复这一过程, 直到前后两次求出的x之差的绝对值小于一个给定的精度。

示例4:设有两个值x0和x1, 令x的初值x0=a/2。程序代码如下:
在迭代过程中, 对方程有解或者无解时应加以区别对待。如果方程有解, 但是迭代公式选择不恰当, 或者迭代的初始近似根选择不合理, 也会导致迭代的失败。如果方程无解, 算法求出的近似根序列就不会收敛, 迭代过程会变成死循环, 所以在迭代之前应首先考察方程是否有解, 并在编写程序时对迭代的次数加以限制。
1.4“打擂台”算法
该算法[1]应用于求解一维数组或二维数组若干个元素的最值问题。其思想是, 将一组数据认为是参与打擂台的比赛者, 先让第一个人站在台上, 第二人上去与之比武, 胜者留在台上。再上去第三个人, 与台上的人 (即刚才的得胜者) 比武, 胜者留在台上, 败者下台。以后每一个人都是与当时留在台上的人比武。直到所有人都上台比过为止, 最后在台上的就是冠军。
示例5:设有一个整型M行N列的二维数组, 找出其最大值

1.5 辗转相除算法
求最大公约数可以用到辗转相除法[18], 也称欧几里德法。设有两整数a和b:
S1:a%b得余数c;
S2:若c=0, 则b即为两数的最大公约数;
S3:若c≠0, 则a=b, b=c, 转向执行S1。示例6所示:
示例6:求a和b两个数最大公约数
if (a<b) //保证a大于b

2 趣味性案例及求解算法
在学习过程中, 常介绍一些趣味性的程序设计题目, 例如猴子吃桃子、求解杨辉三角、n阶魔方阵的问题等。这些题目对提高学生的学习兴趣也起到了至关重要的作用。
还有一些实际应用题目也包含了相应的算法思想, 比如:穷举法求解“百钱买百鸡”问题, 回溯法求解“n皇后”问题等, KMP算法求解“字符串”匹配问题等。
3 结论与展望
上述主要介绍和分析了学生学习C语言过程中几种常用的算法, 并给出了具体实例。另外简单介绍了C语言中的一些趣味性实例对应的求解算法。为了有效地解决实际问题, 不仅需要保证算法的正确性, 还要考虑算法的质量等要素, 所以在编写程序的过程中, 逐步教会或引导学生设计一个正确且有效的算法是至关重要的。
参考文献
[1]谭浩强.C程序设计 (第四版) [M].清华大学出版社.2010.
[2]于清, 吐尔根·依布拉音, 等.算法为先的C语言教学模式探讨[J].计算机教育, 2009 (20) :106-108+96.
[3]屈婉玲, 王捍贫, 段莉华.面向软件工程学科的算法课程建设[J].中国大学教学, 2012 (12) :55-57.
[4]任伟, 任正云.C语言中递归调用的算法研究[J].襄阳职业技术学院学报, 2014 (1303) :27-30+34.
[5]李伟.浅析C语言递归算法[J].电脑知识与技术, 2012 (830) :7229-7235.
[6]闫鑫, 王琴竹.循序渐进学习C语言选择排序算法[J].现代计算机 (专业版) , 2018 (14) :53-56.
[7]孙义欣, 宋大伟.斐波那契数列问题的C语言教学实施探讨[J].电脑编程技巧与维护, 2012 (16) :151-152+154.
[8]白会波, 高瑞平.汉诺塔问题的算法分析及C语言演示程序的实现[J].电脑知识与技术, 2010 (609) :2130-2131.
[9]肖桂云, 袁亚丽.用C语言解决汉诺塔问题的方法及过程分析[J].河北北方学院学报 (自然科学版) , 2006 (03) :71-73.
[10]王敏, 赵晓雷.基于遍历搜索二叉树中最长路径的算法研究[J].现代电子技术, 2010 (3308) :54-55+58.
[11]龚佳, 袁赟, 刘远军.一种二叉树非递归遍历算法的C语言实现[J].电脑知识与技术, 2014 (1001) :223-225.
[12]Stenphen Prata.C Primer Plus (第五版) 中文版[M].人民邮电出版社.2005.
[13]宋美英.基于C语言的冒泡排序算法探讨[J].现代计算机 (专业版) , 2011 (29) :48-49+55.
[14]王敏.改进的双向选择排序算法[J].信息技术, 2010 (3409) :21-24+79.
[15]毛广敏.常用C语言排序算法解析[J].软件导刊, 2012 (1111) :51-54.
[16]李向军, 杨花娥.求解一元三次方程近似根的几种算法的C语言实现[J].西安联合大学学报, 1999 (02) :65-69.
[17]马丽娟.常用计算机算法简介及C语言举例[J].电脑知识与技术, 2010 (611) :2655-2659+2662.
[18]柳小强.基于C语言最大公约数算法的设计与实现[J].现代计算机 (专业版) , 2011 (11) :53-56.





