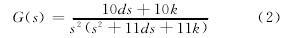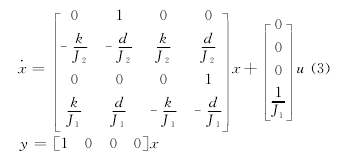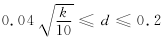当前各个学科相互渗透、相互融合已经成为发展的必然趋势。物理作为一门自然基础学科也不是孤立存在,越来越多地融入了控制理论进行分析。许多物理现象,例如在椭圆轨道运行的人造卫星,小车上的柔杆运动,都可以简化为惯量-阻尼-弹簧系统运动。本文针对惯量-阻尼-弹簧运动进行动力学分析,并利用PID控制方法研究其特性。
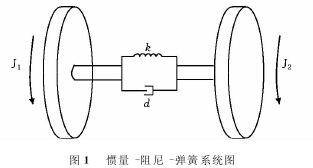
受外加扭矩的惯量-阻尼-弹簧系统的模型如图1所示,其弹簧劲度为k,阻尼系数为d,外加扭矩为TC,转子的转动惯量分别为:J1和J2,转角分别为:θ1和θ2。
1运动建模
由图1所 示,列 出 该 系 统 的 动 力 学 方 程为:
J1¨θ1+d(?θ1-?θ2)+k(θ1-θ2)=TC
J2¨θ2+d(?θ1-?θ2)+k(θ1-θ2)=0(1)
当转动惯量J1=1,J2=0.1时,该系统的传递函数为:
根 据 式1, 选 取 状 态 参 数 如 下:
xT=[θ2?θ2θ1?θ1];式1,可以用矩阵3来表示,其中TC≡u。
为了便于对该系统分析,假设弹簧劲度为k的变化范围:
0.09≤k≤0.4,选取k=0.091;阻尼系数为d的变化范围:
选取d=0.036。矩阵(3)变为矩阵(4)。
2系统稳定性分析
系统能在实际中应用的首要条件是系统要稳定。分析系统稳定性是经典控制理论的重要部分。经典控制理论对与判定一个定常线性系统是否稳定提供了多种方法。本文主要应用Nyquist稳定判据和Bode图判据两种方法来对系统进行分析。
2.1利用稳定判据分析系统稳定性
2.1.1 Nyquist判据
由于一般系统的开环系统多为最小相位系统,P =0,故只要看开环Nyquist轨迹是否包围点(-1,j0),若不包围,系统就稳定。当开环系统为非最小相位系统P≠0时,先求出其P,再看开环Nyquist轨迹包围点(-1,j0)的圈数,若是逆时针包围点(-1,j0)P圈,则系统稳定。
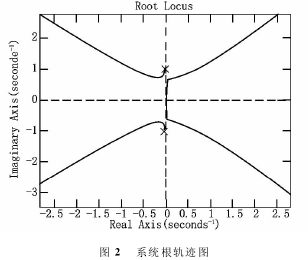
图2是该系统的根轨迹图。从图2可以看出,该系统P≠0,P=1,但Nyqusit轨迹没有包围点(-1,j0),而是放射状,因此该系统不稳定。
2.1.2 Bode图判据Bode图同样可以利用它来判别系统的稳定性。这种方法有时称为对数频率特性判据。对于稳定系统,相位裕度必在Bode图横轴以上,而且要具有相当的稳定性储备。对于稳定系统,幅值裕度必须在0分贝线以下,Kg(dB)>0,称为正幅值裕度,反之,系统不稳定。
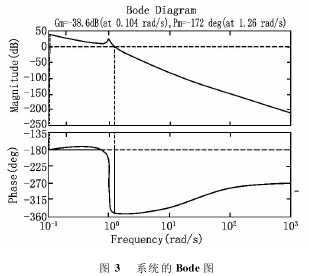
图3是该系统的Bode图。从图3可以看出,该系统相位裕度为-172°,在Bode图之下,具有负的稳定性储备;幅值裕度为-38.6dB,具有负的幅值裕度。根据判据,因此该系统不稳定。
2.2 PID校正设计
由于该系统不稳定,因此在实际中是没有任何应用意义。利用PID控制方法,来实现该系统的稳定。PID调节原理简单,使用方便,且PID补偿系统使之达到大多数品质指标的要求。
由图2和图3所反应的该系统的性能。设计一个微分控制器串联在该系统里。根据理想系统的要求,调试该微分控制器,最后确定传递函数为:
D(s)=0.001(35s+1)。因此该系统的整体传递函数变为:
KD(s)G(s)。
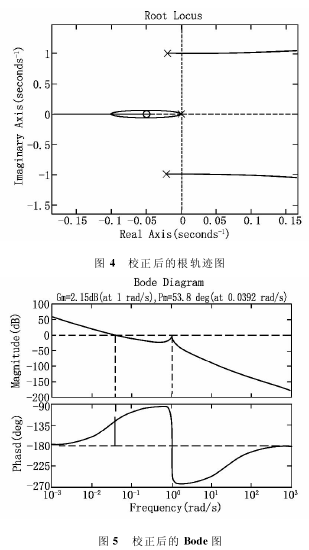
有PID校正后的系统的根轨迹图4和Bode图5。从图4中看出,根轨迹图包围(135,j0)一圈。
符合Nyquist判据对系统稳定性的要求。从图5中看出,校正后系统相位裕度为53.8°,在Bode图之上,具有正的稳定性储备,且储备充足;幅值裕度为2.15dB,具有正的幅值裕度。因此,校正后的系统具有较好的稳定性。
3结论
通过对惯量—阻尼—弹簧系统的动力学建模,利用PID方法对该系统的稳定性进行分析,可以看出,PID校正方法在控制系统的校正中,有着重要的意义,该方法在物理学模型分析中,可以得到广泛应用。
参考文献:
[1] 漆安慎.力学 [M].北 京:高 等 教 育 出 版 社,2006:221-228.
[2] 周衍柏.理论力学教程[M].北京:高等教育出版社,2009:210-224.
[3] 韩建国.现代控制理论[M].北京:中国计量出版社,2007:14-40.
[4] 王银锁.过程控制系统[M].北京:石油工业出版社,2009:21-60.[5] 侯媛彬.现代控制理论基础[M].北京:北京大学出版社,2006:30-36.