摘 要: 多体动力学在现阶段一般是指多体的系统动力学,是一门较为复杂和综合性相对较强的力学学科,在机械工程领域中占据重要地位。结合多体动力学相关概念,介绍多体动力学在机械工程中的应用,为相关工程的应用提供一定的参考。
关键词 : 多体动力学;机械工程;工程应用;
Abstract: At this stage,multi-body dynamics generally refers to multi-body system dynamics.It is a relatively complex and relatively comprehensive mechanics discipline,which occupies an important position in the field of mechanical engineering.Combining the related concepts of multi-body dynamics,introduce the application of multi-body dynamics in mechanical engineering,and provide a certain reference for the application of related engineering.
Keyword: Multi-body Dynamics; Mechanical Engineering; Engineering Applications;
目前,大部分机械系统建设多由多个柔体和刚体部件组成,各种多体系统不仅可以为其提供最为合理和科学的概括,还是多体动力学研究开展的最佳形态。多体动力学研究包含材料力学、生物力学等多门学科,具备高度综合性特征。随着电子计算机技术的不断发展,多体动力学也得到快速发展。多体动力学成为目前机械工程应用研究中最为重要的内容。
1、 多体动力学的相关概述
目前,我们所分析的多体动力学是在机械系统中较为全面和完整的系统模式,具备抽象和概括的特点,因此,需要从多体动力系统模型建设分析多体动力学的主要内容。作为多个学科的融合学科,随着计算机技术的不断发展,将多体动力学结合计算机技术应到工程实践中可以有效促进机械工程的建设和发展[1]。

在机械臂制造、机械制造和航空航天等机械工程中,多体动力学有着十分重要的应用(见图1)。经典的力学原理可以在多个系统中被广泛应用,随后利用微积分方程进行计算和分析。但是,在系统自由度和数量增加的背景下,各个分体之间更加复杂;同时,每个分体之间的约束性相对较强,导致微积分方程的推导十分复杂。为了全面适应现代计算机技术的发展和应用,需要结合经典力学对整个多体系统的作用特点进行全面补充,进而形成一个独特的分支。目前,关于多体动力学及其数学模型的开发方面研究已经有多种方法和形式,这些方法的共同特点是将计算机技术和经典力学相结合。
图1 卫星和机械臂

多体动力学一般由多个刚性物体的运动和多个柔性物体的运动进行相互连接,最重要的组成部分就是结构力学中的多体系统,属于较为完整的高度抽象形式,可以结合一定的途径接触和动态连接多个对象,并且可在MAS中表明,未来发展前景好[2]。
2、 多体动力学模型创建内容
由于机械体的制造是由多个部件组成的,为了实现机械设备的运动,需要对机械装置中的参数进行设定,如机械装置的位移、速度等。
2.1 模型、坐标系和相关定义的约束作用
动力学和运动学是整个多体动力学系统中比较重要的内容,在经典力学解释中,对多体动力学的研究相对复杂,且每个机械零部件本身存在的自由度相对较高、差异性较强,导致部件在位移期间会发生一定的变化,求解微积分运动方程的难度也相对较高,需结合互联网技术进行研究和计算[3]。首先,在机械运动期间选取某2个点运动的建立存在不变特征的物体,再根据刚体上任意一点将其围成一个三角形坐标系,随后将连体基设置在机械部件上。这样,在部件运动期间就可以带动其运动。在该过程中需要明确的是,机械刚体部件的运动对连体基不会造成影响,因此,确定连体基后就已经确定了刚体任意一点的位置。
2.2、 连体基
选取地面为连体基的参考对象,因为地面的坐标系属于固定值,也具备全局坐标的特征。在多体系统中,刚性体和柔性体的坐标定义有序不同。技术人员确定坐标定位后,并不会影响刚体的状态。柔性体部件发生变化后,其本身所在的位置和角、线位移会发生变化,在柔性体上显示出存在的局部问题[4]。构建广义坐标后,求解后续动力学方程的速度也会受到影响。因此,需要技术人员根据广义坐标的转动,将其向余弦矩阵的方向确立后,方可获取坐标系方位的计算过程。在物体转动坐标中,一般采取卡尔丹角或欧拉角作为参考,具有一定的规范性,但随之会提升对奇点附近数值的计算难度。
2.3、 结合余弦矩阵转动广义坐标
为了实现该方法的应用,技术人员可以增加6个方向的约束方程,但是,在进行方程变量求解过程中会存在较大的难度。广义坐标转动对象是欧拉参数时,计算期间不会遇到奇点。为了保障机械要素更加合理,基础约束类部件在10余种,技术人员可结合部件元素的属性进行全面划分,将元素分为部件、约束、分析力模型约束元素等。对不同机械部件进行研究发现,多体动力学中各个部件会产生相互作用,且各个部件的联系模式为拓扑结构[5]。
3 、多体动力学在机械工程中的实践应用
3.1、 机械手臂和动力学分析
工业机器人在目前的机械工程领域中比较常见,甚至已经成为目前机械工程中不可缺少的一部分。工业机器人一般由6个自由度和1个分支组成,各个自由度和分支之间利用刚体连接,形成多体动力学模型。如PUM A760机器人,作为一种比较普遍的机械设备而言,在对该机器人进行研究的过程中,将时间和频率域作为设计基础,首先利用高速摄像机捕捉运动参数,随后将测得的电枢电力值转化为驱动转矩,获取实际运动数据。根据逆运算方式,进一步获取该设备驱动转矩下的平均数值,再将数值进行整合分析,得到静态参数数据,对该数据进行模拟,最终得到设备的物理参数数据,从该设备计算中得到设备的当量阻尼系数和对应的刚性系数。在相关机械设备制作和分析过程中,结合上述模型进行动力学分析可以提升数据计算的精准程度,进而提升数据分析的速度和效果。
3.2、 柔性机械臂的振动控制
在机械工程领域中,柔性机械臂应用极其广泛,比较具有代表性的是在航天领域中轻质重载航天机械臂的使用,可以结合相关指令进行位置跟踪,确定柔性机械臂的端点位置,运动范围较广,精度要求高。但是,在卫星运动期间会受到鞭状天线的困扰,造成振动等问题,因此,需要对柔性机械臂振动进行全面控制。结合构造分析,柔性机械臂属于一种柔性多体系统,可以采取模态法或有限段法控制振动。根据相关实验研究分析,这两种方法的使用可以结合机械臂频率和固有的阻尼系数在特定时间内为端头提供制动力,进而减小和弱化震动效果,提升设备的运动进度[6]。此外,制动力的大小计算是由力学的逆运算决定的,该运算结果也属于最为合适的结果。在此基础上考虑多体系统的动态属性,也可以将端点的形状进行改变,实现全闭环反馈,进而减小柔性臂的振动幅度,提升柔性机械臂在使用中的精度。
3.3 、基于绝对节点坐标法建立柔性梁动力学模型
结合柔性梁动力特点和绝对节点坐标法内容,推导出广义单元弹性力的解析表达式,一维二节点弹性梁单元模型见图2。
图2 一维梁单元变形描述
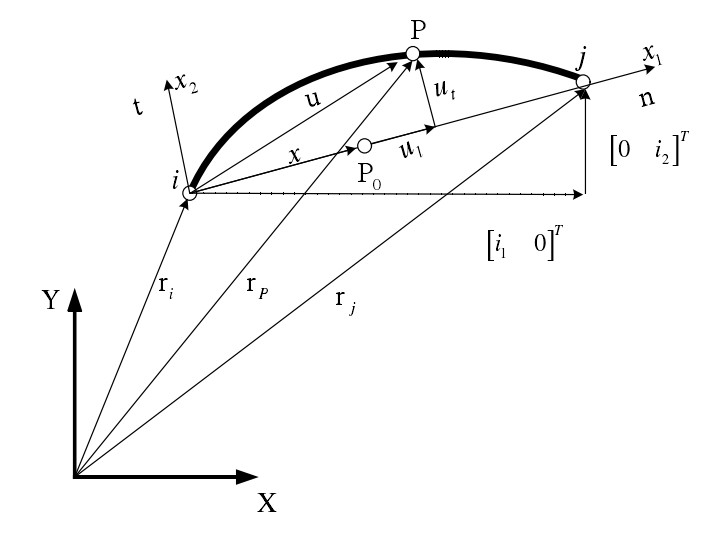
其公式为
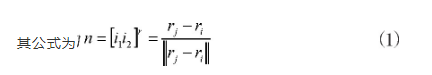
其中,n为单位矢量,i和j表示连接的节点。首先设梁上的一点P0在变形后得到位置P,因此,其位移矢量满足公式:
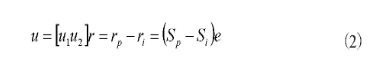
其中,S表示单元形函数,并且在节点i处的形函数矩阵表示为。这时记P点的变形ud、水平方向变形ul与垂直变形方向ut,则满足公式:
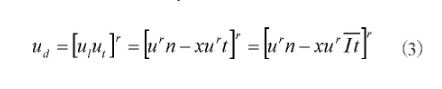
结合本结构关系,其单元的纵向应变可能表示为:

其中的轴向应变表示为:
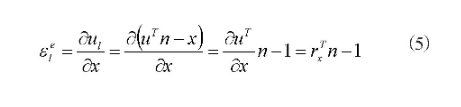
其中,;
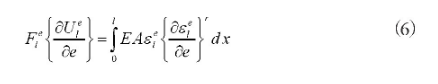
其中单元的轴向弹性力可以利用以下公式表示:
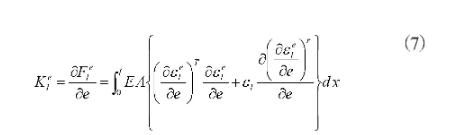
雅可比矩阵可以利用以下公式表示:
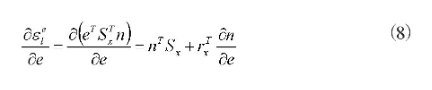
这里面的:

这样单元的弯曲应变能则可以表示为:
其中,k为曲率,表达为,结合弯曲变能公式(4),可以将部件的弯曲弹性计算出来,随后结合单元的弯曲弹性力计算本身的雅可比。最终计算出横向变形引起的单元弯曲弹性力,表示为:。
3.4 、多刚体系统的分析和应用
多刚体系统是目前多体动力学的一个重要分支,研究的基础在于经典物理学,其间的子系统被抽象为刚体形式,内部的弹性变形被完全忽略,但是每个刚体的连接点阻尼和弹性等因素都会对系统产生影响。多刚体动力学研究的主要内容包含物体的位置、姿态、运动和运动中受到的阻力力矩等,涉及的方程包含约束方程和动力学方式,结合矢量力学方法进行推导。其中约束方程主要指结合各种约束模型推导出来的,对物体位置、姿态的限制方程和约束力的释放方程,这样列举出来的方程需要根据矢量运算的规则、姿态和位置关系以及动力学规律进行分析和求解,这也被称为广义坐标,在刚体机械设计中有着十分重要的作用。
4 、结束语
多体动力学主要是结合经典力学的内容和特点,融合现代计算机技术,根据所需要制造的机械工程内容对机械设备进行分析和制造,一定程度上也是结合相关方法计算柔性和刚性机械体的设备参数,根据对参数的分析和计算全面完善整个机械系统。从目前我国对多体动力学研究的成果来看,依然存在不够完善的问题,要想达到刚体和柔体多系统融合发展的目标还需要一定时间的努力。
参考文献
[1]吴军万经济视角下智能化技术在机械工程自动化中的应用[J]工程技术研究, 2020 5(5):33-34.
[2]李道力,于珈懿,高粼泽, 等多体动力学在机械I程领域的应用[J]湖北农机化, 2019(12):33.
[3]刘力瑗多体动力学在机械45号钢加工工程领域的应用[J].世界有色金属, 2017(13):53,55.
[4]温国伟.多体动力学在机械工程领域的应用分析[J]科技视界,2017(13)-89.
[5]佘航宇多体动力学在机械工程领域的应用[J]时代农机, 2017.44(2):42,44.
[6]郭娟.多体动力学在机械工程领域的应用[J]山东I业技术,2016(3):88.





