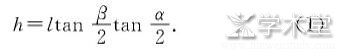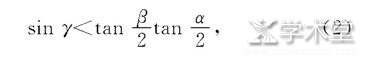动力学论文第八篇:锥体上滚运动实验的动力学探究
摘要:分析了锥体上滚运动的动力学方程, 并通过受力分析方法求解出锥体上滚的条件, 结果与通过能量最低原理得出的结论一致.
关键词:锥体; 上滚条件; 受力分析; 能量最低;
Mechanical analysis of the roll-up motion of cone
SHI Yu-rong MA Li-zhen
Department of Physics, College of Information Science and Engineering, Ocean University of China
Abstract:The dynamic equation of the roll-up motion of cone was analyzed, and the condition of the roll-up motion of cone was obtained by using force analysis method.The results were consistent with those obtained by using the minimum energy principle.
很多科技馆和物理演示实验室有“锥体上滚”实验, 视觉上看到锥体从V型轨道较低的闭口端自动滚到轨道较高的开口端.现有的实验教材和网络资源解释该实验的原理和推导锥体上滚的条件是基于能量最低原理, 表面上锥体沿着轨道上升了, 但是由于锥体本身形状的原因, 滚动过程锥体的重心是下降的.很多学生疑惑哪个力使锥体有水平方向的分运动.本文根据教学过程中遇到过的学生疑惑问题, 分析了锥体上滚运动的动力学方程, 并通过受力分析方法求解出锥体上滚的条件, 结果与通过能量最低原理 (几何方法) 得出的结论一致.
1 利用能量最低原理分析上滚条件
锥体上滚实验没有违背能量最低原理, 锥体上滚是锥体与轨道的形状配合给人以锥体向上滚动的错觉, 仔细观察会发现, 上滚过程锥体的重心是降低的.实际上, 只有当V型导轨夹角、轨道与水平面的夹角调节到合适的角度时, 即达到上滚的条件时, 锥体才会上滚, 锥体滚到轨道最高处时重心最低, 重力势能最小, 所以可以根据重心是否降低来求解锥体上滚条件[1].
锥体上滚的条件与实验装置的3个夹角有关.如图1~3所示, 设锥体顶角为α, 两导轨夹角为β, 导轨平面与水平面间的夹角为γ, 设锥体在轨道上从位置AB滚到位置CD时 (A, B, C, D为锥体表面与轨道的接触点) , 沿轨道角平分线方向前进的距离为l.
图1 过锥体与轨道的接触点和锥体中轴线的截面图
图2 过轨道平面的俯视图
图3 过两轨道角平分线的竖直面
需要特别指出的是, 当求解锥体上滚的条件时, 应先找到锥体不滚动的条件, 也就是锥体放到轨道任意位置处重心高度相同, 此时锥体在轨道任意位置都平衡.
如前所述, 先考虑锥体只下降不滚动的情况, 也就是不受静摩擦力的作用, 同时由于接触面比较光滑, 即使有滑动摩擦力存在也非常小.锥体只受重力和支持力, 此时图1中锥体与轨道接触点和锥体中轴线所在的平面在竖直面内, 则根据几何关系可知:AB位置和CD位置之间的高度差h为
而AB位置和CD位置对应轨道的高度差H为
H=lsinγ.
只要满足H<h, 也就是锥体向开口端运动实际是重心降低, 即
锥体就能从轨道的闭口端向开口端滚动, 也即锥体向低处运动.如果实验装置的γ, β, α这3个角可调, 该结论在实验中很容易观察和验证[2].
2 通过受力分析研究上滚条件
通过受力分析得出锥体上滚的条件需要做简化, 在实验中, 锥体是滚动的, 锥体与接触面之间没有相对滑动, 它们之间的摩擦力是静摩擦力.因为要依据物体滚动的状态判断静摩擦力的方向, 可以先考虑理想的情况.当没有摩擦时, 锥体可以在轨道的任一位置处于受力平衡.这时V型导轨夹角、轨道与水平面的夹角需要满足某种条件.当然从滚动的力学条件来看, 如果有摩擦力, 锥体对质心合外力矩不为零, 它将绕过质心的轴转动, 也即锥体将滚动.这种情况锥体只受轨道给它的支持力和重力2个力, 把支持力分解为水平方向和竖直面内垂直轨道的面的分量.
为了便于说明, 先建立坐标系, 如图4所示, 在水平面内轨道夹角的角平分线的水平分量为x轴, 水平面内垂直该角平分线方向为y轴, 竖直向上为z轴.只要分析出锥体在水平方向所受合外力指x轴的正方向, 锥体就可以向x轴正向加速运动.由于重力在水平方向没有分力, 所以只需分析轨道对锥体的支持力.
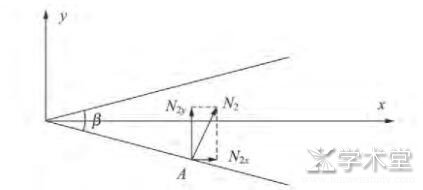
图4 俯视图 (水平面)
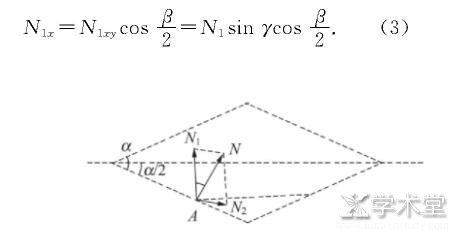
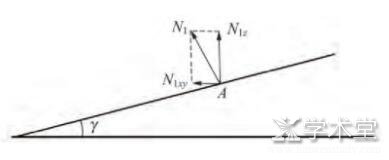
设锥体顶角为α, 两导轨夹角角度为β, 导轨平面与水平面间的夹角为γ, 图5中N表示锥体受到轨道的支持力, 把N分解成垂直轨道的竖直面内的分量N1和垂直轨道的水平面内的分量N2.图6侧视图中的N1为支持力在竖直面内的分量, N1又可以分解成N1z和N1xy, 容易分析出N1垂直轨道与z轴夹角为γ, N1在x轴的分量为
图5 锥体与轨道的接触点和锥体的中轴线决定的平面
图6 侧视图 (过1条轨道的竖直面)
图4俯视图中的N2为支持力在水平面内的分量, N2在x轴的分量为
考虑到锥体与轨道有2个接触点, 只要锥体受到的水平方向合力指向开口端, 锥体就可以“上滚”, 所以锥体上滚的条件表达为
再考虑轨道对锥体的支持力过锥体的中轴线, 如图5双锥体在竖直面的中截面图所示, 可列出方程为
因此由 (5) 式以及 (6) 式得到锥体上滚的条件为 (2) 式.
3 锥体运动的动力学分析
锥体上滚的运动可视为刚体的平面运动[3], 即视为锥体的平动和锥体绕质心轴 (中心轴) 的定轴转动的合成.
3.1 锥体的平动
锥体向开口端平动是因为水平方向有指向开口端的合力, 只要角度调节合适, 可以发现
由 (7) 式可知:
1) 锥体的顶角α确定的情况下, 当β越大, γ越小, Fx越大.
2) 实验时调节V形导轨的夹角β以及导轨与水平面之间的夹角γ, 当满足Fx>0时, 即满足上滚条件 (2) 式, 根据刚体的质心运动定理
锥体就有向开口端平动的加速度.
3.2 锥体的滚动
锥体上滚条件的实质是质心具有了水平向开口端的平动加速度的条件, 也即只考虑了锥体的平动, 实验中锥体做滚动.锥体满足上滚的条件时, 只要它有平动的趋势就将受到静摩擦力, 沿轨道的切线方向指向V型轨道的闭口端, 该力对锥体的质心轴的力矩是动力矩, 使锥体滚动.
关于滚动问题, 也可以把过锥体与轨道的2个对称的接触点当做参考轴, 由于锥体满足上滚条件时, 其质心总在滚动方向上超前锥体与轨道的接触点, 所以重力的力矩对选定的轴是动力矩, 使锥体滚动[4].
4 结束语
通过锥体上滚的受力分析可以看出, 利用守恒定律解释力学问题很简洁, 但是不能给出物体运动的细节情况, 受力分析可以更深刻地展现物体的运动原因.另外, 可以通过百度查到很多物理演示实验的原理, 但是教师应该在教学中充分引导学生用自己的观点解决问题, 也重视学生提出的问题, 从而教学相长.
参考文献
[1]路峻岭.物理演示实验教程[M].北京:清华大学出版社, 2005:7-9.
[2]张锐波.三维可调式锥体上滚演示实验仪[J].物理实验, 2012, 32 (6) :33-34.
[3] 漆安慎, 杜婵英.力学[M].3版.北京:高等教育出版社, 2012:242.
[4]荣振宇, 张莉, 王培吉,等.锥体上滚实验的原因分析[J].大学物理, 2009, 28 (3) :26-28.
点击查看>>动力学论文(最新推荐范文8篇)其他文章