摘要:通过风洞实验研究垂直于来流悬挂的构树叶在025m/s风速段的形态重构现象。根据构树叶分裂情况将其分成心形、单侧分裂、双侧分裂3种, 迎风面正、反面各半。在实验风速段内, 构树叶存在3类形态 (飞翼形、锥形、薄三角翼形) , 主要有3种卷缩方式 (U形、ω形和σ形) .统计数据表明, 树叶分裂情况会在发生概率上影响重构的形态和卷缩方式, 但不会从根本上决定某一形态或卷缩方式的出现。与正面迎风比较, 反面迎风的失稳重构次数减少, 气动性能更佳。叶片角在风速小于6m/s时随风速增加锐减, 然后变化速度减缓, 最后风速大于14m/s后在0°附近几乎不变;随着雷诺数增加, 构树叶的阻力系数减小, 最后稳定于0.05附近。
关键词:构树叶; 形态重构; 叶片角; 阻力系数;
树叶的气动特性的相关研究成果被广泛运用于飞行器的形态设计[1]和新型风力发电技术的研究[2], 因此树叶在风中的振动和变形研究具有相当高的实用价值。
Vogel[3-4]通过风洞实验首次发现:叶柄较长、具有裂片的树叶 (如红枫、鹅掌楸) 或羽状树叶, 在风中具有形状重构的能力;随着风速的增大, 可以自动卷缩成近似流线体的锥状以减小所受的气动阻力并避免出现强烈振动。Miller等[5-6]在水槽中进行实验, 发现一些阔叶植物叶片在较高流速下同样卷成锥形, 且会在锥体内部形成再循环区域进行减振。Speck[7]研究了芦竹在风中的形状重构及迎风面积变化, 证明芦竹也有形状重构减小迎风面积以减小风阻力的能力。Shao等[8-11]发现, 当树叶垂直悬挂时, 杨树、鹅掌楸、梧桐等树叶也出现形状重构现象。此外, 树叶垂直悬挂时在时均气动力的作用下, 叶柄会发生弯曲, 叶片角会发生较大变化。Shao[10]利用天平测试3个方向力和3个方向的力矩, 根据天平测量结果近似计算出鹅掌楸树叶叶片角随风速变化的趋势, 但未在实验证实。
本次实验主要研究构树叶的重构形状和卷缩方式, 并探究构树叶的形状和迎风面的不同对其的影响, 同时记录叶片角和阻力系数的变化情况。
1 实验材料
构树叶为广卵形至长椭圆状卵形, 长6~25cm, 宽5~18cm, 先端渐尖, 基部心形, 不分裂或1~5裂, 柄长2~15cm, 按照分裂情况可分为心形、对称分裂、单侧分裂3类, 是Vogel的研究[3-4]中非常理想的具备形状重构能力的树叶。
实验选用的新鲜构树叶涵盖各种形状, 且均叶柄笔直, 采摘于浙江杭州, 实验时间5月到10月。如图1, 构树叶在自然状态下朝上一面为正面 (光照面) .实验树叶共120片, 三种形状、两种迎风面各20片, 他们的叶片面积、叶柄粗细接近正态分布, 叶柄长度在各类叶型分布均匀。
实验风洞是回流式低速流体力学风洞, 实验段透明, 流速范围为0.5~50m/s, 湍流强度小于0.5%.实验天平是扬州科动电子生产的KD460030系列应变式六分量风洞天平, 量程0~30N.实验使用photronfastcam mini高速相机, 搭配尼康镜头进行拍照。
实验前在风洞实验段顶端中部开一小口, 伸入直径6mm的不锈钢棒, 其上端通过螺丝与测力天平 (六分量天平) 连接并固定, 实验时用细丝线将叶柄端部 (约3cm) 牢固地绑在钢棒下端, 使树叶为垂挂状态, 如图2.
图1 3种构树叶形状Figure 1 Three forms of leaf
图2 叶片在风洞的悬挂方式Figure 2 Sketch of the leaf in wind tunnel
实验开始后用两台高速相机记录叶片的变形和振动, 一台位于侧面, 记录侧视图, 一台位风洞于底部, 记录仰视图, 相机的拍照帧率500s.在两台相机的对应实验段面布置坐标纸, 以便计算叶片角和振动情况。测力天平的采样速率为54kHz.每次实验开始后, 风速从零开始, 风速调整后等待20s待风速稳定后再采集数据。
叶片所受的气动力可分解为流向力Fx (阻力) , 垂直向上的升力Fz, 以及侧向力Fy, 如图3.
图3 叶片受力模型简图Figure 3 Sketch of concentratedaerodynamic load on the leaf
2 实验结果分析
在实验风速段内, 构树叶在时均气动力作用下振、稳交替, 一般存在2到3个稳态 (27%树叶存在4个稳态) , 并以振动的形式 (有时会扭转) 来完成状态调整, 但每一次振动或稳定都不是必须发生。
2.1 正面迎风形态变化
图4是一片正面迎风构树叶的风振过程, (a) ~ (g) 为侧视图, (a′) ~ (g′) 为仰视图。风速较小时, 树叶静态变形, 当风速上升到6.2m/s过程中, 树叶先由平展上包成飞翼状 (U形卷缩) , 然后慢慢形成锥状 (ω形) , 随着风速增大到9m/s, 叶片10Hz上下, 叶梢28 Hz振动, 第一次振动发生。然后在15.9m/s时叶柄扭转, 在17.2m/s时快速重构呈薄三角翼状 (σ形) , 这期间未发生持续性振动。最后风速达21.5m/s时, 薄三角翼状稳定被打破, 叶柄23Hz振动, 叶片5Hz大幅开合, 此时叶梢被吹断, 边缘高速振动 (超过500Hz) , 这是第二次振动。
图4 心形构树叶正面迎风状态变化Figure 4 Front surface facing the wind:status changes with wind speed
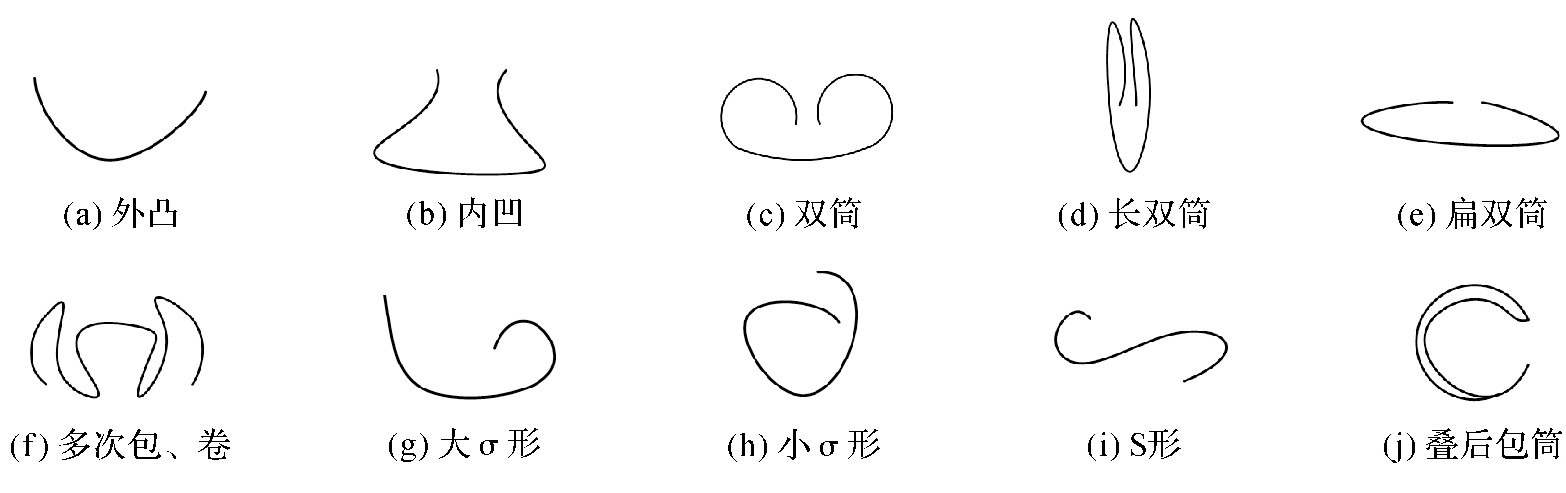
图4的树叶在实验风速段一共出现了3个典型的稳定形态飞翼状、锥状、薄三角翼状。为了更清楚地描述相应的形态, 又定义了三种卷缩方式, 分别是U形 (图5 (a) ~ (b) ) 、ω形 (图5 (c) ~ (f) ) 和σ形 (图5 (g) ~ (h) ) , 此外也存在S形等其他方式 (图5 (i) ~ (j) ) .叶片变化的复杂性和个体的差异性使得卷缩形状千变万化, 因此图5中只列出了典型形状, 实际上它们会存在任意角度的扭转及上、下或左、右的互换。
另外两种形状的构树叶的典型振、稳过程与心形树叶类似, 同样经历叶片上包 (稳态) 、振动、稳定、再次振动、重构稳定、再次失稳这样的历程。它们形成的稳态形状也同样类似。比较特别的是在实验过程中, 一旦发生高频振动, 构树叶很快就会被撕破, 而且被破坏的总是叶梢部分 (图4 (g′) ) .
当然, 树叶形状不同, 他们在风中的振、稳变化必然存在差异。前面已经提到过, 振动与稳定并不是必然发生的, 统计发现心形构树叶出现稳态4的频率最高 (70%) , 它的形态变化最多, 而只有25%的双裂型构树叶存在稳态4, 大部分维持振动2或稳态3直到最高实验风速。不仅如此, 统计数据显示, 树叶形状会影响形变类型和树叶弯卷方式。以正面迎风时稳态2为例, 心形树叶没有出现U形、飞翼状稳态, 其他各截面形状比例相当;单裂型树叶以ω形、锥状为主, 各种形状均有出现;双裂型54.4%的ω形、锥状, 36.4%的σ形、薄三角翼状, 剩下9.1%为U形、飞翼状。
不同的稳定阶段构树叶的典型稳态也有区别, 表1是正面迎风的构树叶4个稳定状态的典型整体形状。从稳态1到稳态4, 树叶的形变基本遵循先包再扁的规律, 薄三角翼状的树叶会因多次包、卷形成锥状, 不过绝大部分的薄三角翼状稳定的树叶都会在之后的振动阶段被撕破。
图5 典型卷缩方式Figure 5 Sketch of typical rolling-up way
表1 三种形状构树叶正面迎风各阶段典型形状Table 1 Typical forms of 3shapes in different steadies with the front surface facing wind
2.2 迎风面对形态重构的影响
反面迎风时形态重构没有正面迎风那么多, 表2中处于最大实验风速时, 只有7.1%的反面迎风树叶处于稳态4 (没有树叶处于稳态4之后的状态) , 而正面迎风树叶在该风速处于稳定4及其后的状态的树叶占比为38.7%, 即:迎风面的不同影响构树叶状态变化的进程, 与正面迎风比较, 反面迎风会延缓甚至消除某些会在正面迎风时出现的状态。比较正、反面构树叶的风振历程后发现, 超过一半的正面迎风的构树叶或前或后发生了叶柄的扭转, 而仅有2片反面迎风树叶有叶柄扭转现象, 同时它们的形态重构也较多。
如果把开始出现振动1、稳态2、振动2、稳态3、振动3的风速分别称为第1, 2, 3, 4和第5临界风速, 并分别用V1, V2, V3, V4和V5表示, 表3给出正、反面迎风时5个临界风速的期望值, 很明显反面迎风的各个临界风速均比正面时要大, 这从另一个方面说明反面迎风会延缓相关状态的出现。
反面迎风时典型的树叶形状和弯卷方式与正面迎风时一致, 但是在出现频率上有区别。同样是稳态2, 反面迎风的心形树叶出现了飞翼形稳定, 单裂型没有出现飞翼状, 双裂型树叶中75%的都是锥形。
表2 正、反面迎风树叶在最高风速时所处状态统计Table 2 Statistics of the leaf status at the highest wind speed
表3 正、反面迎风各临界风速的期望值Table 3 Expected values of each critical wind speed
2.3 叶片角和阻力系数随风速变化
如图2定义叶片长度方向与来流的夹角 (忽略在垂直来流的平面上的分量) 为叶片角, 用θ表示。实际中取构树叶中脉线三分之一点 (构树叶叶梢如图2在风中上扬) 附近的切线方向与来流方向的夹角。
3种叶型正、反面迎风6片树叶的叶片角随风速的变化如图6 (图6和图7中A、B、C, 分别表示心形、对称分裂、单侧分裂, f、b分别表示正面与反面迎风) , 他们的变化曲线都在风速6m/s前锐减, 然后变化速度变缓, 中间可能会因为状态的变化出现一定的波动, 最后在风速14m/s后基本稳定在某较小的角度附近 (相当于水平, 因为构树叶中脉前段本身存在弯曲) .
图6 叶片角随风速变化Figure 6 Blade angle of leaf vs wind speed
定义叶片阻力系数Cx为
式 (1) 中 为相应风速下的时均阻力, ρ表示空气密度, V∞为实时风速, S为叶片的平展面积[4] (用切割法近似计算, 误差不大于4cm) .
定义雷诺数
式 (2) 中ν为空气运动粘度, L为叶片长度。
从图7可以看出, 叶片不同, 阻力系数也不尽相同, 但他们的变化趋势相似:风速较小时, 阻力系数较大, 随着风速增大, 雷诺数增加, 阻力系数减小。当雷诺数大于8×10以后, 阻力系数变化幅度很小, 最终在2.6×10后稳定于0.05附近。振动会引起阻力系数的小幅波动。
图7 阻力系数随雷诺数变化Figure 7 Drag coefficients of leaf vs Reynolds number
3 结论
在0.5~25m/s的实验风速段内, 垂直来流悬挂的构树叶在时均气动力作用下振稳交替, 不过每一次振动或者稳定都不是必须发生的, 大部分的树叶只出现部分状态。
随着风速的增大, 构树叶重构的形态基本遵循先包再扁、再包、再扁这样的规律, 以不断减小受风面积。重构形态可分飞翼形、锥形、薄三角翼形3类, 其中飞翼状一般在风速较小时出现;卷缩方式主要有U形、ω形和σ形3种, 也存在S形等其他形式。叶片尾流的旋涡脱落频率与叶柄或叶片的固有频率接近时, 树叶发生高频大幅振动, 构树叶尾极容易被撕破。
统计数据表明, 树叶分裂情况会在发生概率上影响重构的形态和卷缩方式, 但不会从根本上决定某一形态或卷缩方式的出现。与正面迎风比较, 反面迎风时树叶难以发生扭转, 形态重构次数减少, 气动性能更佳。阻力系数和叶片角随风速增大而减小, 表现了构树叶良好的重构减阻能力。
参考文献
[1]岑海棠, 陈五一。仿生学概念及演变[J].机械设计。2007, 24 (7) :1-2.CEN H T, CHEN W Y.Conception and evolvement of bionics[J].Journal of Machine Design, 2007, 24 (7) :1-2.
[2]HADHAZY A.Power plants:Artificial trees that harvest sun and windto generate electricity[J].Scientific American, 2009, 306 (5) :31-32.
[3]VOGEL S.Drag and reconfiguration of broad leaves in high winds[J].Journal of Experimental Botany, 1989, 40 (8) :941-948.
[4]VOGEL S.Leaves in the lowest and highest winds:temperature, force and shape[J].New Phytologist, 2009, 183 (1) :13-26.
[5]MILLER L A, SANTHANAKRISHNAN A, JONES S, et al.Reconfiguration and the reduction of vortex-induced vibrations in broad leaves.[J].Journal of Experimental Biology, 2012, 215 (15) :2716-2727.
[6]MILLER L.Reconfiguration of broad leaves into cones[J].IEEE Transactions on Magnetics, 2013, 49 (7) :4168-4171.
[7]SPECK O.Field measurements of wind speed and reconfiguration in Arundo donax (poaceae) with estimates of drag forces[J].American Journal of Botany, 2003, 90 (8) :1253-1256.
[8]SHAO C P, CHEN Y J, LIN J Z.Wind induced deformation and vibration of a platanus acerifolia leaf[J].Acta Mechanica Sinica, 2012, 28 (3) :583-594.
[9]邵传平, 朱园园。鹅掌楸树叶在风中的变形与振动[J].力学学报, 2017, 49 (2) :431-440.SHAO C P, ZHU Y Y.The deformation and vibration of tulip Leaves in Wind[J].Chinese Journal of Theoretical and Applied Mechanics, 2017, 49 (2) :431-440.
[10]SHAO C P, ZHU Y Y.The steady and vibrating statuses of tulip tree leaves in wind[J].Theoretical and Applied Mechanics Letters, 2017, 7 (1) :30-34.
[11]朱园园, 邵传平。鹅掌楸树叶气动特性研究[J].中国计量学院学报, 2015, 26 (4) :411-415, 422.ZHU Y Y, SHAO C P.Experimental investigation on the aerodynamic characteristics of liriodendron leaves[J].Journal Of China University of Metrology.2015, 26 (4) :411-415, 422.