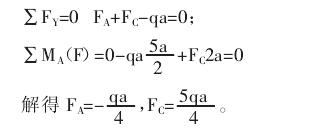0引言
工程力学中,直梁的弯曲变形是杆件受力变形的基本形式之一,在对梁进行强度和刚度计算时,通常要画出剪力图和弯矩图,以便清楚地看出梁的各个截面上剪力和弯矩的大小、正负以及最大值所在截面的位置[1].但不少学生在学习剪力图和弯矩图绘制知识点时,直呼太难,根本不知从何下手。因此,总结出一套行之有效的简易绘制剪力图和弯矩图的方法,显得越来越重要。下面就结合作者实际教学经验,提出解决此类问题的简易方法。
1绘制剪力图和弯矩图的简易方法
绘制剪力图和弯矩图时,应严格遵循下列基本步骤:
①画梁的受力图,求约束力 求出梁上所有约束部位的约束力是至关重要的第一步,这一步如果出现问题,后续步骤基本进行不了,关于求约束力的方法,在画好受力分析图后列平衡方程式即可求得。
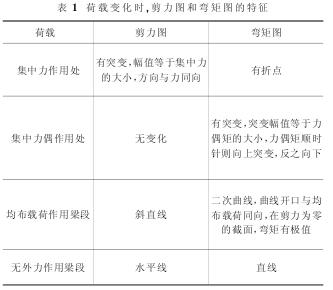
②画剪力图。画剪力图时,应牢记下面几句话:集中力作用处,剪力图有突变,突变幅值等于集中力的大小,突变的方向与力的方向同向;集中力偶作用处,剪力图无变化;均布载荷作用的梁段上,剪力图为一条斜直线;无外力作用的梁段上,剪力图为水平的直线。
对于剪力图为斜直线,只需确定直线的两个端点所对应的剪力值即可确定该直线,要求两个端点所对应的剪力值,采用某截面上的剪力值等于截面左边梁上所有外力的代数和,外力向上,则剪力为正,反之为负的方法。
③画弯矩图 画弯矩图时,也须牢记以下几句话:集中力作用处,弯矩图有折点;集中力偶作用处,弯矩图有突变,突变幅值等于力偶矩的大小,力偶方向若为顺时针,则弯矩向上突变,反之向下突变;均布载荷作用的梁段,弯矩图为二次曲线,曲线开口方向与均布载荷同向,在剪力为零的截面,弯矩有极值;无外力作用的梁段,弯矩为直线。
对于弯矩为二次曲线的,只需取曲线上三个特殊的点,求出该点所对应截面的弯矩值即可确定该曲线,而求某截面上弯矩值,采用某截面上的弯矩值等于截面左边梁上所有外力矩的代数和,外力矩为顺时针的,弯矩为正,反之为负的方法。
当荷载发生变化时,剪力图和弯矩图特征如表1所示。
2实例分析
图1所示外伸梁AB,在CB段作用均布载荷q,试画此梁的剪力图和弯矩图。
解:①画梁的受力图,求约束力。
先对梁进行受力分析,受力分析图如图2所示。列力学平衡方程式:
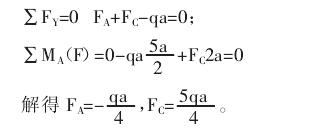
②画剪力图。
由于A截面上作用向上的集中力FA,故A截面上的剪力值由零突变为-qa∕4;
AC截面之间为无外力作用的梁段,故该梁段上的剪力图为水平线,也即是该梁段上的剪力值保持A截面突变后的剪力值不变为-qa/4;
C截面上作用向上的集中力FC,故C截面上的5qa/4为qa;
CB截面之间为均布载荷作用的梁段,故该梁段上的剪力图为斜直线,确定C+截面(此截面为无限靠近C截面,但在C截面右侧)的剪力值为qa和B-截面(此截面为无限靠近B截面,但在B截面左侧)的剪力值为0,即可确定该直线;
B截面的剪力值为0;
故可画得外伸梁AB段的剪力图如图3所示。
③画弯矩图。
由于集中力作用处弯矩图有折点,所以A截面的弯矩值M(A)=0;
AC梁段为无外力作用梁段,所以弯矩图为直线,只需确定A+截面的弯矩值和C-截面的弯矩值即可确定该直线,可求得M(A+)=0,M(C-)=FA2a=-qa²/2;
C截面作用集中力FC,故M(C)=M(C-)=-qa²/2;
CB梁段为均布载荷作用梁段,故弯矩图为二次曲线即抛物线。因为均布载荷方向向下,故抛物线开口向下,又因为剪力为零的截面,抛物线有极值,所以可知B截面上的弯矩值最大。由于M(C+)=M(C)=-qa²/2,从而可大致画得该抛物线。
画得外伸梁AB段的弯矩图如图4所示。
3结语
以上内容是笔者根据自身实际教学经验,对工程力学中剪力图和弯矩图绘制知识点所总结出来的行之有效的简易方法,只要学生在学习过程中始终遵循以上基本步骤,熟练掌握求任意截面剪力和弯矩值的方法,熟记表一中荷载变化时,剪力图和弯矩图之特征,则力学中所有剪力图和弯矩图都可采用此简易法绘制出来。不仅提高了解决此类问题的能力,同时调动学生学习的积极性,提高教学效果,为培养既具有创新能力又具备工程实践经验的高素质技术技能型人才打下良好的基础[2].
参考文献:
[1]王瑞清。《工程力学》中剪力图和弯矩图的快易绘图法[J].科技资讯,2011(34):32-33.
[2]龚友根。浅谈工程力学中的受力分析问题[J].价值工程,2012(1):49.