摘要:随着我国教育制度的不断放开, 高校的财务管理难度也日益加大, 因此, 优化和完善高校的财务管理评价体系已经成为当务之急。但是由于评价体系存在着一定的客观性, 无法定量, 经过学者的不断研究, 对于这类问题采用了模糊数学的方法, 从而将定性的评价因素转换为定量的形式, 帮助高校更加了解自身的财务管理情况, 从而及时发现并解决问题。
关键词:模糊数学; 高等院校; 财务管理; 评价体系;

一、引言
近年来我国开始实行鼓励社会化自主办学, 这一政策的出现为我国的高校教育创造了新的机遇与挑战。高校因此而获得了更多的自主管理的权力, 尤其是在财务运营方面, 高校自身能够自主地作出一定的财务决策, 正因如此, 这样的政策一方面可以帮助高校更好地去发展自身, 树立自身的特色和品牌, 另外一方面也对高校的财务运作能力和监管制度提出了更高的要求。据数据显示, 在“十三五”期间, 我国的高校总负债金额已经高达3?000多亿, 江苏省作为教育大省, 共有137所高校, 平均每所高校的负债也超过5亿元, 这个数字对于很多高校而言, 已经超出了其承受范围。在广东甚至出现了高校贷款180亿元共同建立大学城的现象, 虽然其中有150亿元由政府承担, 但是剩下的30亿对于高校来说也是巨额贷款了。由此可见, 如何在新形势下抓住机遇, 科学地发展高校教育之路, 要求高校的管理人员在如何保障学校财务工作的规范运作、如何更好地监控财务工作等方面下功夫, 从而保证高校财务工作的平稳、合法、合规的运行, 这已经成为高校财务管理的重中之重。对此, 高校应当建立科学的财务管理评价机制, 对于校内的财务工作进行分析和客观评价, 及时发现财务管理工作中存在的风险及隐患, 这是当下高校应当关注的。
要建立科学的财务管理评价体系中最重要的环节就是评价指标的选取。由于高校财务管理运作中的风险因素具有客观性、相关性以及随机性的特点, 在选取指标的时候应当将相关的评价因素全面地纳入到考虑范围中, 并且对于各项评价因素的重要性进行客观的评价, 从而更好地做好评价指标的选取工作, 为财务管理评价体系的建立打下坚实的基础。由于高校的财务运作及管理工作具有不确定的特点, 因此, 如今许多学者提出了通过模糊数学的方法对高校财务管理的工作进行评价, 帮助高校财务人员和管理者对本校的财务管理机制进行优化。本文中也将对这一方法在财务管理工作中的运用进行阐述。
二、模糊数学
模糊理论 (Fuzzy Theory) 原理是通过数学的方法对具有“模糊性”特征的客观现象进行处理与研究, 因此也被人们称为“模糊数学”。在模糊理论中对日常生活中所遇到的各种变量进行分类, 可以分为确定性和不确定性两类, 而不确定性根据其特点又分为模糊性变量和随机性变量, 我们每个人也是通过这三种数学变量来观察这个世界的。根据量的分类, 可以将数学模型相应分为三类:第一, 确定性数学模型。这一模型是对具有确定性的量进行研究, 各量之间存在着必然的关系。第二, 随机性数学模型。这一研究模型, 研究对象具有随机性, 此外, 对象之间的关系呈现偶然性的特征。如概率分布法建立的数学模型。第三, 模糊性数学模型。这一模型, 是对相互之间具有模糊性关系的对象进行研究并建立科学的数学模型。
量{确不定确性定性——{—随模经机糊典性性数——学————随模机糊数数学学
在人们的印象中, 数学是一门要求精确的学科, 但现实生活中, 存在很多模糊的东西, 无法给出一个确定的数字, 因此需要对模糊概念进行一定的量化, 再使用数学方法对其进行研究。原理如下:对于边界以及外延不明确的概念, 如“好”与“坏”等, 在数学里难以隶属于一个集合, 此时用[0、1]中的某个数字来表示其隶属程度。
三、模糊数学在高校财务管理中应用的可行性
(一) 指标的模糊性与模糊集合论思想的一致性。
财务指标可用精确数字来表示, 具有精确性的特点, 非财务指标则是模糊的。但从以下几个角度来看, 财务指标在一定程度上来说也具有模糊性:第一, 由于很多财务数字是需要依据单位当前的发展形式以及当前市场的情况来做决策, 带有一定的主观性, 因此会计数据的产生并不是百分百客观的;第二, 由于经济业务的变动会导致会计要素随之发生改变, 从而导致实际变动的数据与通过各种会计方法所计算得到的数据之间存在着一定的差距, 所以财务指标虽然是精确的数字, 但这并不代表它就是精确的, 而是围绕着现实情况不断波动的。
(二) 模糊数学在财务评价体系应用领域的适用性。
一是财务评价这个过程本身带有模糊性, 因为财务评价体系从建立到后期的执行都具有主观性, 较为复杂, 无法用精准的数字来描述, 但这正是模糊数学所研究的领域, 在看似杂乱无章的事物中, 找到其特有的规律性。二是评价高校财务管理需要对其收支状况等进行分析研究, 收支状况等财务管理指标与财务评价两者之间没有明确的界限, 除此之外, 影响高校财务管理水平的因素众多, 而且相互之间也不存在确定关系, 是模糊的, 因此财务评价体系完全符合模糊数学所研究的范畴, 能够更好地评价高校的财务管理状况。
(三) 模糊数学实践技术的可行性。
模糊数学之所以会诞生, 就是在那些没有明确定性的问题研究与数学方法之间搭建了一座桥梁, 并且在实际的财务管理中, 模糊数学已被普遍运用。因此, 使用模糊数学来对高校财务管理进行评价, 以此来检测高校现行财务管理的有效性, 从而可以根据评价结果不断优化自身财务管理方法及模式, 帮助高校更好发展。
从以上三个角度可以看出, 将模糊数学应用到高校财务管理中具有极高的可行性的, 模糊数学一方面对于评价指标的设定不需要一个绝对标准, 克服了单一指标所带来的片面性的缺点;另一方面, 模糊数学通过所谓的“模糊”手法使得评价更加精确, 因此模糊数学在高校财务管理中的应用是值得不断发展和深入研究的, 对于高校财务管理模式的转型和优化起着较大的推动作用。
四、基于模糊数学的应用———以高效科研资金管理评价为例
(一) 评价指标的选取。
通过模糊数学来对高校财务管理进行评价时, 必须先确定好科学的财务评价指标体系, 将这些指标定义为因素集U, 在建立高校科研资金管理评价体系时, 其主要测量指标则为集合U, 设一级指标为U={U1, U2, U3}。利用层次分析法, 来确定隶属于每个一级指标下的二级指标, 例U1={U11, U12, U13}, U2={U21, U22, U23}等。在指标选取的这一过程中要遵循以下原则。
1. 可操作性。
建立高校科研资金管理评价体系是为了能够利用这一体系更好地对学校的老师及其科研经费使用情况进行绩效考核, 因此选取的评价因素必须简洁、易获得, 方便员工操作这一体系。指标的数据可以通过公式计算或者调查、统计等方式获得, 为评价体系打下基础。
2. 全面性。
评价体系的指标选取要真实、完备。只有评价要素齐全, 能够覆盖高校科研资金管理的各方面, 才能够科学、全面的反应其管理水平的真实情况, 暴露其存在的问题, 否则, 无法达到应有的效果。高校每年的科研经费巨大, 且科研经费虽然有一定的自主支配权, 但也需要注意做到专款专用, 只能用于科研项目, 因此对于科研经费管理的评价较为复杂。既要能够反映高校科研经费支出的结构是否合理, 又要反映其在科研工作方面的效率性, 从而更加全面地考核高校科研经费的管理水平。此外, 在指标选取的过程中, 应当尽量保证指标之间的独立性, 避免出现重叠现象, 对评价结果造成影响。
3. 满足各利害相关方的不同财务信息要求。
在选取指标时必须要考虑到各个利益相关方, 不能只考虑高校管理人员或仅考虑国家宏观政策, 只有将相关的利益方都考虑在内才能全面对高校科研经费管理现状进行分析, 否则, 所获得的信息也只是片面的, 不能很好地指导高校进行管理优化。
综合以上的要求, 在科研经费管理评价体系中可设置以下指标作为评价主要因素。
(二) 设置评价集。
设置评价集合为E, 对高校科研经费管理评价指标体系中的各评价因素进行单因素评价, 如设E={E1, E2, E3, E4}来表示对该项活动的评价, 分别代表“很好”、“好”、“一般”和“差”, 设定好评价分类之后, 可以咨询高校的财务人员, 对这一评价标准设定标准, 此处假设评价标准用{0.9, 0.8, 0.7, 0.6}来表示。
图1
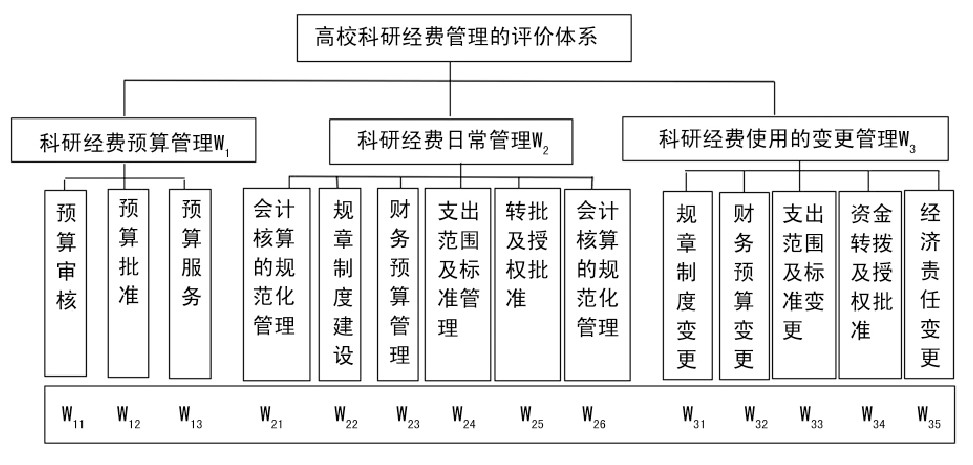
(三) 设置各项因素的权重。
权数的设置影响每个评价因素在整个体系中作用的大小, 在确定因素权重时必须要科学合理。对于权重的设置可以采用专家调查法, 即“德尔菲预测法”来确定, 就是根据高校财务人员及相关教职工提供的有关评价指标的资料, 将资料交由若干名相关方面专家、学者进行审阅, 请他们在资料的基础上, 结合自身的经验给出权重的建议, 对每一个指标, 将专家所建议的权重进行加权平均, 从而得到各层次评价指标的权重数。如图1所示, 用W1, W2, W3表示第一层的权重, 用wi1, wi2, …wim表示第二层权重。通过专家对每个指标的评价集E进行打分所占比重, 可得评价矩阵Rin, 即Rin=Wi*ET
通过运算确定综合评价结果, 由第二层级每个因素在评语集上的隶属度Rin与相应基层二指标的权重分配集相乘, 得出中间模糊评价矩阵Ri, 即Ri=Rin*[wi1, wi2, wi3, …wim]将Ri组成矩阵R, 再根据U上各因素分配权重W, 则得到第一级的综合评价结果为:S=W·R。根据所得的结果判断出目前高校科研经费管理体系中各项指标的满意程度, 及时发现不足因素, 帮助高校优化自身管理机制, 提高管理水平。
五、结语
通过上述研究可以看出由于财务管理中的模糊性等特点与模糊数学研究对象的特点相吻合, 因此利用模糊数学将财务管理评价中的定性类的指标进行定量化, 解决了评价体系中难以量化的不确定性问题。因此, 运用模糊数学建立高校财务管理评价体系有利于规范高校的财务运作, 帮助高校不断优化自身管理水平, 使得各项经费能够更加高效地运用, 真正提高学校教育水平、科研水平, 从而为学生提供更好的教育质量。
参考文献
[1]张静, 张乔.关于高校财务实行绩效预算管理的探讨[J].教育财会研究, 2007, 5
[2]韩正忠等.模糊数学应用[M].南京:东南大学出版社, 1993
[3]李慧.基于模糊聚类的经济责任审计评价方法研究[J].财会月刊, 2012, 9
[4]戴立新, 李雪松, 刘颖.基于模糊综合评价法的电力建设项目采购管理绩效评价[J].财会通讯, 2009, 10:34~36
[5]龚建英.普通高校财务风险管理研究[D].长沙理工大学, 2006:16~18
[6]陈珍.高校财务风险评价指标体系研究[J].云南财贸学院学报, 2006, 3





