
一、引言
采购经理人指数 PMI (Purchasing Managers’ In-dex)是目前欧美国家常用的监测宏观经济运行的先行指标。 欧美国家的政府部门、金融机构、企业等经济主体常用其预测经济转折点、判断未来经济运行态势、分析不同产业信息、研究金融市场运行走势等。 AnthonyJosepha (安东尼·约瑟,2011)等认为制造业 PMI 变化会影响到央行货币政策决策以及金融市场走势。
E-van F. Koenig(埃文 F.柯尼希 ,2002)认为 PMI 能够预测制造业增长、经济运行拐点以及美联储政策变化。当PMI 高于 47%时,制造业活动处于扩张阶段;当 PMI 高于 50%时,整体经济处在活跃阶段;当 PMI 高于 52.5%时, 美联储通常调升短期利率。
Matthew D. Lindsey(马修 D.林赛,2005)等利用 PMI 数据 ,建立回归模型能较好地预测商业周期的变化。
进入新世纪,国家统计局、中国物流与采购联合会先后共同编制出制造业 PMI(2005 年)、非制造业 PMI(2007 年)。 国内制造业 PMI 是基于制造业采购经理调查问卷的结果编制而成,目前此项调查问卷涉及了 12个问题,包括了生产量、新订单、出口订货、现有订货、采购量、进口、产成品库存、原材料库存、购进价格、从业人员、供应商配送时间以及生产经营活动预期等。对上述每个问题可以分别计算扩散指数,即选择“升高/增多”的企业家数百分比加上选择“持平/不变”的百分比的一半。 由于制造业采购经理调查问卷的主要调查内容与企业采购关系紧密, 企业采购作为日常生产经营的前置环节,其行为如何发生、何时发生、发生规模将支配企业乃至整体经济活动的发展趋势。 因此,PMI对于反映当前经济运行和未来经济发展趋势具有较高的可靠性。
现在,不仅中央电视台、新华社等国内着名媒体都抢在第一时间转发 PMI 指数,理论界、研究机构、金融机构等也都将 PMI 指数作为经济分析研究决策的核心数据使用。
在采购经理人指数与物价的相关性研究方面,于颖(2009)指出我国制造业 PMI 购进价格分类指数对工业生产者出厂价格指数(PPI)具有明显的先行性,领先期为 3 个月, 时差相关系数高达 0.94, 属高度正相关。
张道德、俞林(2009)建立向量自回归模型,发现制造业 PMI 综合指数对居民消费价格指数(CPI)存在正向的推动作用,但作用较小。
王勇(2009)研究认为,美国、欧元区、日本等经济体的 PMI 与国际市场的铅锌价格都具有短期均衡关系,通过观察 PMI 指数的变化能预测出铅锌价格走势。
李跃辉、彭嘉莹(2013)通过建立向量误差修正模型和格兰杰因果关系检验, 发现我国制造业 PMI 综合指数分别是 CPI、 消费者信心指数的格兰杰成因,PMI 综合指数对 CPI 具有正向作用。
张宁、陈晴旖(2013)建立了制造业 PMI 综合指数与PPI 的 VAR 模型,实证发现 PMI 综合指数对 PPI 具有很好的预测作用,PMI 综合指数的提高会促进 PPI 下降。
笔者认为,在分析预测 PPI 方面,制造业 PMI 购进价格分类指数的效果好于制造业 PMI 综合指数。 主要理由是,从指标的设计上看,制造业 PMI 购进价格分类指数较制造业 PMI 综合指数能更好观测到工业品价格变化。 制造业 PMI 购进价格分类指数的编制基础是样本企业采购经理在 “本月主要原材料价格的平均购进价格比上月上升/变化不大/下降”上的选择,一般情况下企业为维持正常生产经营, 购进价格波动会较快地传导到相关工业品价格。 相比之下, 制造业 PMI综合指数是由新订单、生产、从业人员、供应商配送时间、原材料库存等 5 个分类指数加权计算而成(各分类指数的权重分别为:新订单 30%、生产 25%、从业人员20%、供应商配送时间 15%、原材料库存 10%)。 这 5 个分类指数与工业品价格的联系密切程度不一, 新订单分类指数、生产分类指数、原材料库存分类指数与工业品价格的波动虽有一定关系, 但这种关系更多带有间接性。更重要的是,现阶段国内企业用工规模的调整与工业品价格升降的联系趋小,主要是随着国内“刘易斯拐点”来临,受新增劳动人口持续下降的影响,就业市场供求关系趋紧, 国内制造企业尤其沿海制造企业普遍处在缺工状态。 因此,从理论上看,制造业 PMI 购进价格分类指数较制造业 PMI 综合指数, 与 PPI 存在更密切的关系。
二、指标选取及指标走势
将制造业 PMI 综合指数记为变量 PMI, 制造业PMI 购进价格分类指数记为变量 PMI_GJ,PPI(当月同比价格指数)记为变量 PPI。 笔者采用月度数据,样本区间为 2005 年 1 月~2014 年 3 月, 数据来源于 WIND数据库,使用 EVIEWS6 软件进行实证分析。
从图 1 可以看出,2005 年以来我国制造业 PMI 综合指数、 制造业 PMI 购进价格分类指数和 PPI 都出现了数次较大幅度的波动, 而且在国际金融危机爆发前后波动更加明显。 从三者波动的幅度看,2005 年 1 月~2014 年 3 月,制造业 PMI 购进价格分类指数波动最大(标准差为 9.7%),PPI 其次 (标准差为 4.4%),制造业PMI 综合指数最小(标准差为 3.1%)。 从三者波动的走势看,制造业 PMI 综合指数、制造业 PMI 购进价格分类指数的波峰、波谷领先于 PPI。 通过计算时差相关系数,可以发现制造业 PMI 购进价格分类指数变化明显超前于 PPI,在领先 4 期,两者时差相关系数最大,达0.74, 可以初步认为制造业 PMI 购进价格分类指数变化比 PPI 超前了 4 个月。 在 0 期到领先 6 期, 制造业PMI 购进价格分类指数与 PPI 的时差相关系数均高于制造业 PMI 综合指数与 PPI 的时差相关系数, 这也说明在分析预测工业品价格变化方面,制造业 PMI 购进价格分类指数更优于制造业 PMI 综合指数。【图1】

三、实证分析
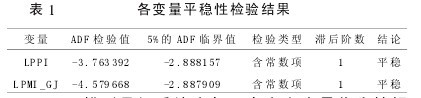
(一)平稳性检验由于现实经济生活中实际经济变量数据有可能是非平稳的,如果直接对非平稳序列建立回归模型,即使模型拟合度很高, 但由于模型的残差序列还是非平稳的,会使所建模型无法准确预测未来信息。 因此,为保证回归结果的有效性, 必须对各经济变量进行平稳性检验。 笔者采用 ADF(Augmented Dickey-Fuller test)检验法来判断变量的平稳性。在平稳性检验前,为消除数据中可能存在的异方差问题,对变量 PPI、PMI_GJ 取对数,分别记为变量 LPPI、LPMI_GJ。 表 1 是各变量平稳性检验情况,可以看出,在 5%的显着性水平下,变量LPPI、LPMI_GJ 拒绝原假设,即接受不存在单方根的结论。 因此,变量 LPPI、LPMI_GJ 都是平稳序列。【表1】
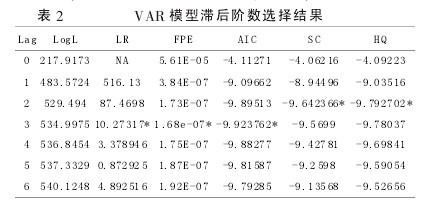
VAR 模型是把系统内每一个内生变量作为被解释变量、 所有内生变量的滞后值作为解释变量来建立的模型, 通常用于预测可能存在相互性的经济变量系统,通过探讨随机扰动对变量系统的冲击,来解释各种冲击对不同变量所产生的影响。在建立 VAR 模型的过程中,滞后阶数的选择和确定是关键问题。 一方面,模型的滞后阶数越大, 越能反映出所构造变量系统的动态特征;另一方面,随着滞后阶数增多,待估计的参数将增加,模型的自由度相应减少。 因此,确定滞后阶数需考虑上述两方面的因素。 从表 2 可以看出,5 个检验标准中,LR、FPE 和 AIC 这 3 个标准都选择滞后阶数3,笔者确定最优滞后期为 3。 以 LPPI、LPMI_GJ 为内生变量,常数 c 为外生变量,建立 VAR 模型。【表2】
(三)协整检验协整检验用于检验系统内变量之间是否存在长期稳定的均衡关系。 如果检验发现变量间存在长期稳定关系,就能排除单方根造成的随机性。协整检验的常用方法有 EG 检验法和 Jonhansen 检验法。 笔者采用Jonhansen 检验法,由于协整检验的滞后期为无约束条件的 VAR 模型一阶差分变量的滞后期,结合前述确定的无约束条件的 VAR 模型最优滞后期是 3,笔者协整检验的滞后期选择 2。 进行协整检验的前提条件是系统内各变量必须有相同的单整阶数, 上述的平稳性检验已表明变量 LPPI、LPMI_GJ 都是零阶单整过程,可以进行协整检验。表 3 是变量协整关系的检验结果,可以看出, 在 5%的显着性水平下, 变量 LPPI、LPMI_GJ之间存在 1 个协整关系, 反映出变量 LPPI、LPMI_GJ之间存在长期均衡关系, 使用变量 LPMI_GJ 对变量LPPI 进行预测是可行的。【表3】

根据协整向量的系数估计值, 可以得到协整关系所对应的长期方程为:【1】
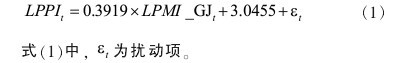
由式(1)可以看出,从长期而言,制造业 PMI 购进价格分类指数每上涨 1%,将拉动工业生产者出厂价格指数上涨 0.3919%。 由式(1)可推导出方程的误差修正项为:【2】

经检验, ECMt是平稳的,其取值在 0 附近上下波动, 这再次验证了变量 LPPI、LPMI_GJ 之间协整关系的存在。
(四 )向量误差修正模型 (Vector Error Correction,VEC)的构建VEC 模型是对系统变量施加了协整约束条件的向量自回归模型。 由于变量 LPPI、LPMI_GJ 之间存在协整关系,可以建立 VEC 模型。 VEC 模型的滞后期选择与协整检验相同,所建立的 VEC 模型如下:【3】

从式(3)可以看出,工业生产者出厂价格指数的短期波动可以分解成两个部分:一部分是滞后一阶、滞后二阶的工业生产者出厂价格指数和制造业 PMI 购进价格分类指数短期波动带来的影响,其中,滞后一阶的工业生产者出厂价格指数系数最大,为 0.6401,说明短期内工业生产者出厂价格指数在上涨(或下跌)过程中存在较大的惯性; 另一部分是误差修正系数对长期均衡的调整,由于该误差修正系数为-0.0634,故当变量的短期波动偏离长期均衡时, 误差修正项以负向修正的方式将非均衡状态拉回均衡状态。
(五)格兰杰因果关系检验协整检验说明变量 LPPI、LPMI_GJ 之间存在长期均衡关系,但它们是否具备因果关系,还要进行格兰杰因果关系检验。 如果变量 LPMI_GJ 有助于预测变量LPPI, 即根据变量 LPPI 的滞后值对变量 LPPI 进行回归时,再加上变量 LPMI_GJ 的滞后值,可以显着增强回归模型的解释能力,则称变量 LPMI_GJ 是变量 LPPI的格兰杰成因;反之亦然。表 4 是各变量格兰杰因果关系检验情况, 可以看出, 在 5%的显着水平上, 变量LPPI不是变量 LPMI_GJ 的格兰杰成因,而变量 LPMI_GJ是变量 LPPI 的格兰杰成因。 可见,制造业 PMI 购进价格分类指数是引起工业生产者出厂价格指数变化的原因。【表4】

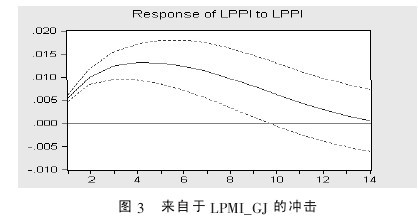
(六)脉冲响应分析脉冲响应分析反映的是系统中一个内生变量的冲击将对各个内生变量造成的动态影响。 用脉冲响应分析衡量来自变量 LPPI、LPMI_GJ 的意外性外生扰动对变量 LPPI 的影响程度与影响时间。 从图 2 可以看出,在本期给变量 LPPI 一个正冲击后, 变量 LPPI 立刻有一定的反应,增加了 0.0054,此后连续增长 3 期并在第 4期达到最大值(0.0131),第 5 期后影响随时间推移逐渐减小, 这表明变量 LPPI 受到外部条件的某一冲击后,不会形成持续稳定的增加或减少。从图 3 可以看出,当本期给变量 LPMI_GJ 一个正冲击后, 变量 LPPI 在本期没有发生变化, 但随即连续增长 7 期并在第 7 期达到最大值(0.0113),第 8 期后影响随时间推移逐渐减小。【图3】
(七)方差分解方差分解是通过分析每一个结构冲击对内生变量变化(一般用方差度量)的贡献度,来评价不同结构冲击的重要性。 为反映变量 LPMI_GJ 对变量 LPPI 变动的解释力度,对变量 LPPI 不同预测期的误差进行方差分解。 随着预测期的增加,变量 LPPI 对自身变动的贡献率从第 1 期的 100%持续下降, 在第 12 期之后趋于平稳, 基本稳定在 57%; 同时变量 LPMI_GJ 对变量LPPI 的贡献率由第 1 期的 0 逐期增加, 在第 12 期之后也趋于平稳,大体稳定在 43%,可见,中长期看制造业 PMI 购进价格分类指数对工业生产者出厂价格指数的变动有较高的贡献度。 这也说明制造业 PMI 购进价格分类指数对工业生产者出厂价格指数的预测作用十分显着。
四、结论
第一, 通过计算时差相关系数、 比较指数走势情况,结合指数的编制特点,在分析预测 PPI 变化方面,制造业 PMI 购进价格分类指数更优于制造业 PMI 综合指数。
第二,通过构建 VAR 模型、VEC 模型,并进行协整检验、格兰杰因果关系检验等实证分析,结果显示,制造业 PMI 购进价格分类指数与 PPI 之间存在长期均衡关系, 购进价格分类指数是引起 PPI 变动的原因,对PPI 有正向冲击作用,对 PPI 的变动也具有较强的解释力度。从长期来看,购进价格分类指数每上涨 1%,将拉动 PPI 上涨 0.3919%。 因此,通过观测制造业 PMI 购进价格分类指数的升降来预测 PPI 变动是可行的。
鉴于制造业 PMI 购进价格分类指数能够对 PPI 进行较为有效的预测, 企业可以根据购进价格分类指数的升降,更好地安排生产、销售以及库存,更恰当地进行产品定价,以实现企业经营效益的最大化;政府也可以通过制造业 PMI 购进价格分类指数对 PPI 进行预测与分析, 提高对行业生产、 工业品价格等调控的科学性,以保持全社会物价平稳运行。





