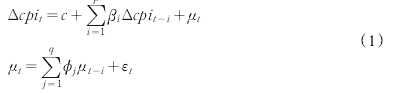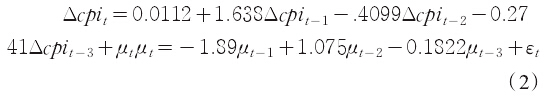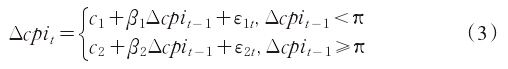0 引言
当前我国正处于经济转型期,过去几十年中长期粗放型型的发展方式已经无以为继,其中最具有显性的现象就是通货膨胀的加剧,房价高涨与城镇化工业化进程中土地、资本、劳动力成本上涨带来的物价上涨已经让人民的生活受到了巨大冲击。另外物价的高企是受到众多因素所决定的,比如人民币升值、进出口贸易结构、宏观财政与货币政策的调整等等。但无论如何,任何一个时间序列的波动在一定时段内总是特殊规律的表现,是可以通过一定的数理方法进行模拟和预测的。在学术界,针对时间序列的预测成果非常多,在这里并不一一叙述,仅以居民消费价格指数的预测列出一些代表性的成果,如李璇和黄冬冬(2013)使用ARIMA模型对2000年1月至2012年12月的CPI月度数据,发现ARIMA(3,1,3)模型能够很好的拟合该序列。王宇等人(2009)使用BP神经网络分别预测出2008年和2009年我国CPI序列进行了预测。查进道(2012)采用逼近思想建立DE-SVR拟合模型,并使用该方法对居民消费价格指数(CPI)进行预测。董梅(2011)将原料、燃料和动力购进价格指数与CPI指数一起列入分析范畴,建列了向量自回归模型(VAR)进行了预测。本文认为时间序列是线性与非线性规律的结合,在预测过程中不能仅以线性或非线性方式进行考虑,所以采用组合方法更能够提高精度。本文使用体现线性规律的移动平均自回归模型与体现非线性规律的BP 人工神经网络模型进行组合,形成ARIMA-BP 模型,进行 CPI 预测。同时采用门限自回归(TAR)模型进行拟合预测,对两种模型的拟合精度进行对比。
1 居民消费价格指数预测分析
1.1 基于ADF和PP的数据平稳性检验
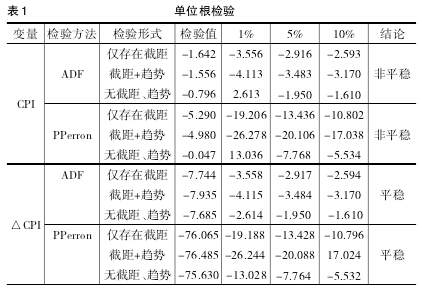
对于时序数据的预测与其他分析,需要数据具有同分布性质。对于这样的要求,通常的时间序列并不满足的这样的要求,因为序列波动会受到其他随机扰动冲击的干扰。所以在实践中只要满足矩条件就能够认为其平稳,具体为序列当期和滞后期间的协方差只与两个时点之间的间隔有关,而与当期无关。目前平稳性检验方法主要有修正的迪克-付勒(ADF)和菲利普斯-陪荣(PP)两种,\使用上述方法对我国2008年1月至2013年8月间的我国居民消费价格指数(CPI)进行单位根检验,分析软件为stata11.0。
无论采用哪种检验方法,有三种形式:存在截距、存在截距和趋势项、不存在截距,具体选取应根据赤池准则(AIC)和施瓦茨准则(SC)确定。表1显示两种检验方法、三种检验形式均在5%显著性水平下接受存在单位根的原假设,说明序列非平稳,而经过一阶差分后,两种方法三种形式在1%临界值水平上的检验结果为平稳,故认为CPI序列服从I(1)过程。
1.2 移动平均自回归——BP神经网络预测
移动平均自回归模型是以当期CPI为被解释变量,自身的滞后变量和随机误差项的滞后项作为解释变量的回归过程。方程为:
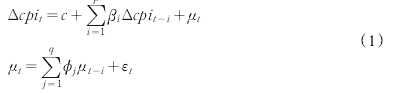
(1)表明△CPI的t期值受到其自身滞后p期影响,且随机误差项为均值为0、标准差自回归阶数为q时得到扰动项为定值的白噪声序列。对于p和q的确定,一般称为识别过程,可以通过偏自相关图和自相关图进行确定。图1显示PAC系数在滞后3期内相对较大,在以后各期整体相对较小,故认为AR(3)过程,图2为AC系数,在滞后3期截尾,故认为选取的模型为 ARIMA(3,1,3),估计结果如(2)式。
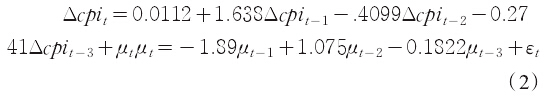
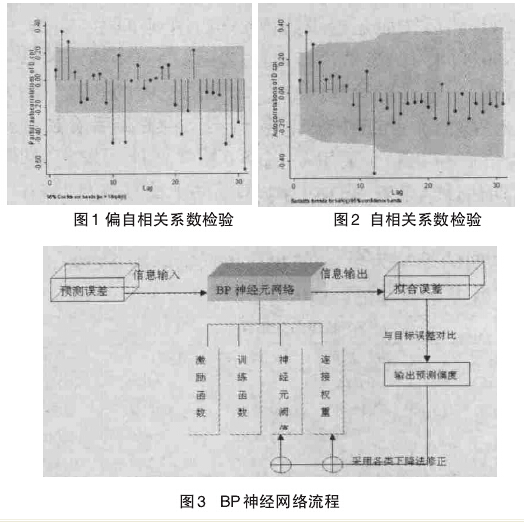
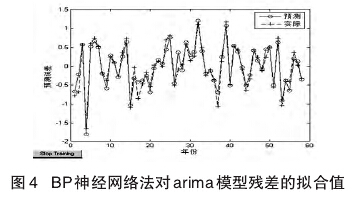
使用上述ARIMA模型预测得到拟合值CPI*与误差序列resid,雷可为和陈瑛(2007)认为移动平均自回归模型体现的是时间序列的线性变动特征,而对于一些因随机冲击导致的非线性规律则无法体现。而这些随机冲击并不具有严格的统计学规律,所以使用高度迭代性质的误差逆向传播修正算法(人工神经网络BP)算法对非线性误差进行预测,然后再将误差结果与线性结果结合,会大大的提高拟合精度。本文采取resid序列滞后1-9期为输入矩阵,当期值为输出变量,首先介绍BP神经网络算法:该算法主要是依据信息的前向传递与误差的逆向传播与修正为基础,使用梯度下降理论对神经元之间的连接赋权值和各节点自身的阈值进行调整,最终目的是为了使非线性误差的预测精度提高,主要结构如下:一是需要确定神经元层数,一般而言使用1个神经元层就已经足够(在不显著神经元个数的情形下);二是神经元个数,目前学术界无规定规则,一般采取10为初始值,三是训练函数与激励函数。信息输入后BP网络会根据一定的函数形式进行处理后再信息输出,输入层、中间层函数一般取S型对数logsig,输出层的使用函数purelin,训练法选为共轭梯度法trainscg。(图3)在设置学习次数为 100 次,学习系数为 0.05 后,执行Matlab7.0软件的网络训练,结果显示在训练100次后误差降低到0.01左右,精度非常高。图4给出了ARima模型预测得出的残差序列与BP网络训练后得到的预测残差序列拟合图,可以发现重合率和一致性都非常高。
1.3 门限自回归模型分析
因为CPI序列为一阶单整序列,所以采用△CPI进行建模。建模形式为:
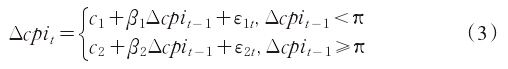
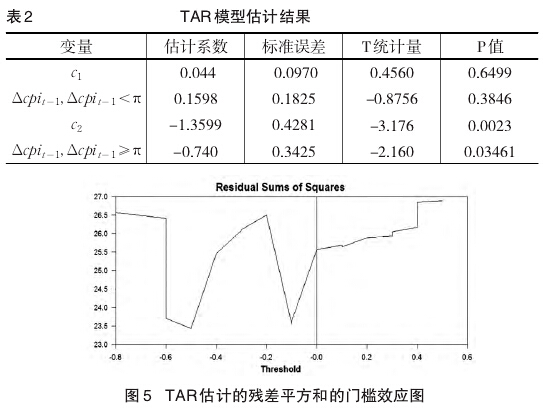
TAR模型由华人经济学家汤家豪提出,基本思想是在单时序数据区间内引入j-1个门槛值,从而将序列划分为j个区间,然后按照延迟步数将数据归纳到不同区间内,再对不同区间内的数值进行自回归。这里需要确定的是三个指标:一是滞后阶数的确定,二是门槛值的选取。因为△CPI序列为一维随机游走序列,本文设置滞后阶数为1,门槛值π=-0.50。采用winrats8.0软件估计后发现,从滞后1期估计结果看,当CPI序列的波动上涨具有自抑制性,即当滞后期的波动值大于-0.05时,△CPI每增加1个百分比给当期的影响为负(-0.740),相反影响为0.1598。图5给出了残差平方和的门槛效应图。
1.4 两种模型对比分析
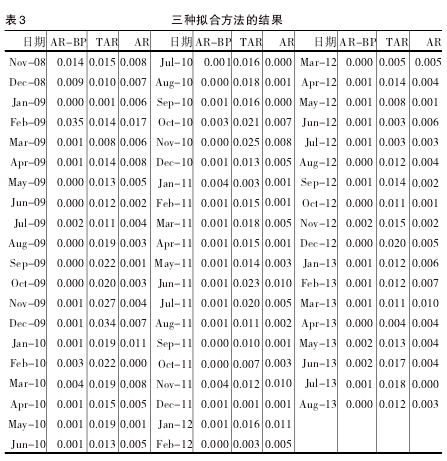
将表2的估计参数代入(3),求出△CPI的拟合值△CPI*,然后将Δcpi*t+cpit-1,还原出TAR模拟得到的预测序列,表3给出了2008-11月至2013年8月三种预测模型给出的 CPI 预测结果,本文计算相对预测误差结果为:
AR-BP 模型为 0.197%,TAR 模型为 1.388%,ARIMA 为0.454%。预测精度排序为AR-BP>ARIMA>TAR。在众多研究中,普遍认为非线性时间序列具备的结构突变效应注定了传统ARIMA计量模型会失效,为了大大提高预测精度,非线性时间序列回归方法被引入,但本文以居民消费价格指数进行拟合后发现,CPI序列呈现出线性规律占主体,而非线性规律为辅助,所以对于时间序列分析不可一味的认为复杂非线性算法比普通方法更能达到精度的渐进提高。
2 总结
物价上涨已经引起了全社会的极大关注,尤其是在一些关系国计民生的产品类型上,如粮食、蔬菜、日用必需品、交通通信价格上。政府通过各种措施对物价加以控制不仅有利于宏观经济政策的实施,更有助于维持社会经济秩序和人民生活安宁。所以有必要对CPI的波动规律加以挖掘和进行预测,当然选择合适的方法是前提,本文通过实证分析发现,采用同时反映线性和非线性规律的ARIMA-BP组合方法比单纯的使用线性ARIMA和非线性门限自回归模型所得到的预测结果精度要高,同时ARI-MA预测效果高于TAR也说明了物价波动过程中线性规律要大于非线性规律。同时非线性拟合方法中的BP神经网络与TAR模型的机理也不尽相同,前者没有严格的统计学基础,仅依靠信息的输入输出强行训练出一套符合实际的预测网络,而后者则具有相应的统计学机理,本文认为非线性规律一般都不符合特定的统计分布,所以除非能够检验出序列具有明确的非线性统计规律,否则使用非线性回归就不能很好的体现出随机冲击效应,这也为预测研究过程方法的选取提出了一点借鉴。