
0引言
针对调查数据的聚类分析算法,现阶段国内外的学术专家都在研究该算法体系,从不同的方面提出了相差各异的运算方法。冯超运用DBI聚类指标并且用最大最小距离的方法来进一步获取最佳聚类数目,曾志雄把K-均值聚类算法的有效性以及层次聚类算法的精确性两大优势相结合,建立了一套具有高效率的混合聚类算法,最大程度上的解决了K-均值聚类算法以及层次聚类算法的运用难题[2].范光平则是建立了一套关于变长编码的改良遗传算法和K-均值聚类算法相互结合,还考虑到初始聚类中心的优化和最佳聚类数目K值的学习体制,很大的解决K-均值聚类算法对初始中心选择敏感以及聚类数目K值的难题[3].孙士保也提出了利用加权方法改变K-均值聚类的算法,主要功能就是能够减少噪声数据以及孤立点数据对聚类结果的影响,并且还能解决带有符号属性的数据问题[4].徐益峰提出了一类有关数据对象在空间分散规律的全新类聚分析方案,此方案能很好地解决因为初始中心选取的随意性而形成的不稳定的聚类结果问题[5].
本文利用K均值算法在聚类分析过程中出现的问题,提出了一类有关相似度优化计算以及指标加权优化的改良算法,并且将此算法应用到了货源投放的零售终端中。
1K均值算法的缺陷分析
K均值算法首先要选取k个点作为初始聚类中心,其次就是要计算出每个数据对象到每个聚类中心之间的距离,将数据对象划分为离它最近的聚类中心区域中;对于经过改进后的新型计算聚类中心算法来说,若相近两个聚类中心之间没有一定的改变,那么表示数据的对象的调整过程已经结束,聚类准则函数Jc也已经收敛。此算法框架如下图:
(1)设置一个固定的n的数据集,并且令I=1,选取k个初始聚类中心Zj(I),j=1,2,3,…,k(1)
(2)计算每个数据对象和聚类中心的之间的距离D(xi,Zj(I)),i=1,2,3,…,n,j=1,2,3,…,k(2)假如符合D(xi,Zj(I))=min{D}(xi,Zj(I)),i=1,2,3,…,n(3)那么xi∈wk.
(3)计算k个新的聚类中心Zj(I+1)=1n∑i=1njx(j)i,j=1,2,3,…,k(4)(4)判断:假如Zj(I+1)≠Zj(I),j=1,2,3,…,k,那么I=I+1,返回式(2);否则,算法结束。
根据上述的算法思维以及算法架构,我们可以清楚的了解到,k个初始聚类中心点地选择过程对于聚类结果的产生会形成一定的影响,因为在这个算法中是随意选择K个点来作为初始聚类中心的原因,如果有一定的经验,那么能够选取具有特征的点来进行操作。
综上的算法过程中,一次次迭代过程就是要将每个数据对象划分到距离它比较近的聚类中心区域中区,在此过程中的时间复杂度设为O(nkd),该处n的含义是数据对象的总个数,k是指确定的聚类数目,用d来表示数据对象的维数;全新的分类形成以后需要计算全新的聚类中心区域,在此过程中,O(nd)来作为时间复杂度的标志。所以此算法一次迭代的总时间复杂度为O(nkd)。
2K均值算法的优化
2.1相似度计算优化
K均值算法的要求就是用户自定义聚类个数k值,在聚类分析的过程中很容易选取最优化的局面。该文在这个算法中相似度的计算方法是使用原本的欧式距离度量方式,下面是较为具体的算法:
(1)假如一个包含n个数据对象的集合Sn,Sn={x1,x2,…,xn}.第一步选择距离最大两个数据对象w、v作为初始的聚类中心:dwv=max{dij,i,j∈1,2,…,n}(5)假设x*1=xw,x*2=xv,dwv=d*1;
(2)将集合Sn中的多余n-2个数据对象,根据欧式距离计算并且按照x*1,x*2来进行聚类中心的分类,如下式?i∈{1,2,…,n/w,v}(6)假如符合式(7),那么将xi划分到类x*1中,否则将xi划分到类x*2中,这样就将集合Sn按照x*1,x*2来进行聚类中心的分类,记作S*21,S*22.|x|i-x*1<|x|i-x*2(7)
(3)计算类S*21中的所有数据对象到x*1的距离,得出d21=max{|xi-x*1|,xi∈S*21}(8)计算类S*22中的所有数据对象到x*2之间的距离,得出d22=max{|xi-x*2|,xi∈S*22}(9)选取d*2=max{d21,d22},相应的数据对象记为x*3.
(4)假如d*2>hd*1(h为输入参数,往往由经验获得),选取x*3作为第三个聚类中心点,将Sn以x*1,x*2,x*3为类中心划分成了三大类,分别记作S*31,S*32,S*33.
(5)算出类S*31中的所有数据对象到x*1之间的距离,得出d31=max{|xi-x*1|,xi∈S*31}(10)算出类S*32中的所有数据对象到x*2之间的距离,得出d32=max{|xi-x*2|,xi∈S*32}(11)算出类S*33中的所有数据对象到x*1之间的距离,得出d33=max{|xi-x*3|,xi∈S*33}(12)d*3=max{d31,d32,d33}(13)相应的数据对象记为x*4.
(6)假如d*3>h?average(d*1+d*2),那么将x*4作为第四个聚类中心点,返回式(4),否则算法结束,最终得到聚类中心为x*1,x*2,x*3.
2.2指标加权优化
使用欧式距离针对K均值算法进行优化之后,考虑到这种因素的影响,实施者总是会因为注重某种指标而忽略了整体效果,因此就需要给这些指标赋予一定的权重,这样做是为了让改良聚类结果可以发挥更大的作用。
假如三点m、n、s的p维向量坐标是(xm1,xm2,…,xmp)、(xn1,xn2,…,xnp)、(xs1,xs2,…,xsp),符合(xs1,xs2,…,xsp)=(xm1,xm2,…,xmb+c,…,xmp)(14)其中,1≤b≤p(b∈Z),c为常数。
依据两点之间加权欧氏距离定义得出下式:


由于主观经验加权欧氏距离具有较强的主观能动性和自主性,因此本文中将变异系数法加入到聚类分析的过程中去,根据数据的特征进行聚类分析。
假如n个样本p维向量的矩阵形式如下:
3算法实例仿真
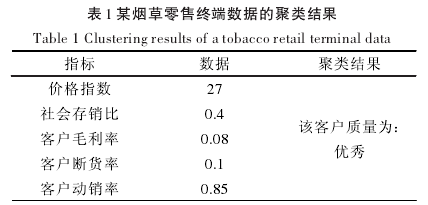
为了证明本文中提出的算法在零售终端数据聚类分析过程中是科学可行的,针对该算法进行检测。将某烟草零售终端的销售数据作为例子,实验的指标就是价格指数、社会存销比、客户毛利率、客户断货率以及客户动销率,聚类结果如表1.
依据聚类的数据分析,按照这个客户制定的货源投放的策略是作为:客户具有优先使用资源的权利。从实验的数据中可以得到结论,本文提出的改良K均值算法在零售终端数据聚类分析中是科学可行的。
4总结
本文提出了关于改进K均值算法的聚类分析模型,该模型主要是对零售终端数据进行数据的开发利用,把卷烟的品牌正确投放作为标准,来维护卷烟市场的正常运作顺序。努力优化市场化取向下的地产公司卷烟营销工作的形式,最大程度上提升了资源利用的专业水平。





