
迈克尔逊干涉仪是一种利用分割光波振幅的方法实现干涉的精密光学仪器。它将一束光分成两束,经过不同路径再相遇时,只要两束光的光程差小于该光的相干长度,一般将会在干涉场中产生干涉现象。自 1881 年问世以来,迈克尔逊曾用它完成了三个着名的实验:否定“以太”的迈克尔逊—莫雷实验;光谱精细结构;利用光波波长标定长度单位。
目前,学生实验主要观察激光、钠光的等倾、等厚干涉现象,并测量光波波长、钠双线的波长差等。白光是由不同颜色的光复合而成的,大部分位置各种颜色的光干涉叠加导致视场中一片亮光,看不到干涉条纹。只有在特定很窄的区域中才可看到干涉现象。所以白光干涉实验只是要求观察干涉现象。利用白光干涉对玻璃折射率或厚度的测量同学们很少接触。徐等报道了利用单色光源测定厚透明材料的折射率。蔡等报道了利用汞灯测量透明薄片的厚度。文章利用普通的白炽灯作为白光光源,选用不同厚度的石英玻璃,利用玻璃置于光路前、后干涉条纹的移动确定玻璃的折射率,检测试样的光学参数。将不同厚度的玻璃置于两反射光路中分析出现白光干涉的极限情况。
1 实验原理
如图 1 所示,这是实验最常用的迈克尔逊干涉原理分析图,面光源 S 经 M1、M'2反射后产生的干涉可由两路光的光程差 Δ 解释。当 M1、M'2严格平行时,所得的干涉为等倾干涉,倾角为θ(θ 很小) 的入射光线最终在 E 上形成明暗相间的同心圆干涉条纹,其光程差为:Δ = 2d cosθ式中:
θ 为光线在 M1镜面的入射角,d为M1与M'2间空气薄膜的厚度。【图1】
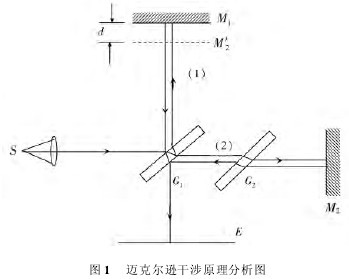
干涉条纹的级次以中心为最高,在中心处θ= 0,如果不考虑因材料造成的反射光线相位的突变,中心出现明暗条纹的条件是:【1】
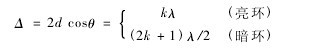
式中:k 为条纹级次,λ 为光的波长,d 的变化将会引起条纹的吞吐变化,当 d 逐渐减小,小到几乎为零时,在 d 的一个很小的变化区域内会出现白光的干涉条纹,白光的等倾干涉条纹为彩色的同心圆,当条纹中心处出现黑色条纹时为绝对零光程处,即Δ = 0。
如果在分光板 G1与 M1镜之间平行于 M1镜放置一块厚度为 d'、折射率为 n 的透明平薄板玻璃,保持 M2镜位置不变,通过调节 M1镜的位置,才能再次出现白光干涉。由于 n > 1,故加入薄板后,经M1镜反射的光路光程增大,而经M2镜反射的光路光程不变,此时若要出现白光干涉图样,需减小前者光程,使之再次达到零光程差。即 M1镜移动Δd 引起的光程变化 2Δd 应等于置入此透明平薄板引起的光程变化 2(n - 1)d'。故有:n = Δd / d' + 1(1)因此,要想求得折射率,只需利用迈克尔逊干涉仪测出 Δd 即可。
2 实验仪器
实验所用的仪器:迈克尔逊干涉仪、钠光灯、白炽灯、毛玻璃屏、石英玻璃
3 实验结果与讨论
光路中未放置石英玻璃片,和将待测石英玻璃片与M1镜镜面平行放置于光路中后,均通过调节迈克尔逊干涉仪在视场中观察到彩色干涉条纹,分别记录两次彩色条纹的对称中心在视场正中时的 M1镜位置 d1、d2。采用多次测量法以减小实验误差,结果如表 1 所示。【表1.略】
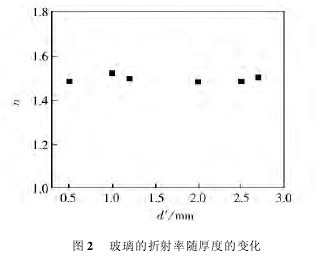
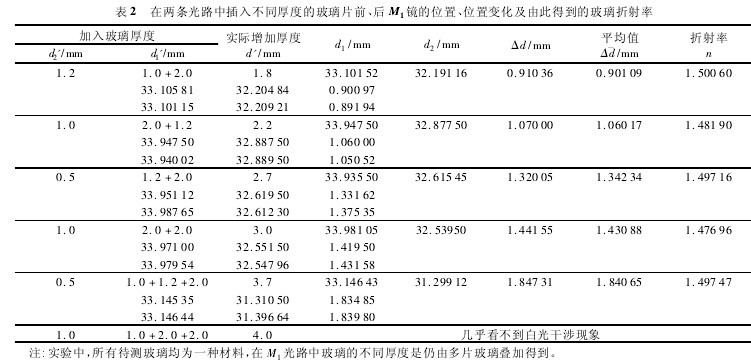
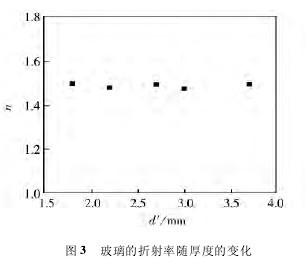
根据式(1) 计算得到材料的折射率。图 2 给出了材料的折射率随玻璃厚度的变化曲线。可以看出:厚度为 0. 5 mm 和 2. 0 mm 的玻璃片折射率基本一致,而由这两个厚度组合成的2. 5 mm 的玻璃片,其折射率正好位于 0. 5 mm 和 2. 0 mm 的玻璃片折射率之间,说明了测量结果的可信性。厚度为 1. 0 mm 的玻璃片折射率高于 1. 2 mm 的,且二者均高于 0. 5 mm 和 2. 0 mm 的。2. 7 mm 是由 1. 2mm、1. 0 mm、0. 5 mm 三个厚度叠加得到,其折射率值介于0. 5 mm 和1. 0 mm 的之间也是很容易理解的。此外,当玻璃片叠合成的厚度为 3. 0 mm 时,几乎观察不到干涉条纹。我们分析:白光在镜面及玻璃面的多次反射、散射损失掉一部分能量,玻璃也会吸收一部分能量,玻璃表面的平整性,这些因素均会影响两束光相遇时光强大小。实验时只在M1镜光路上加玻璃片,由于玻璃片的存在,使得此光路的光强度比M2镜光路的光强度有明显削弱。两路光的光强相差较大,导致相干性差,从而几乎看不到干涉条纹。同时也使能得的玻璃片的厚度范围受到了限制。为了证实这一点,我们又设计了下述方案:在 M1镜和 M2镜光路上分别加上平行于 M1镜和 M2镜的玻璃片(厚度分别为 d'1和d'2),使得两束光光强削弱程度相差不大,减小两束光相遇时发生干涉的光强差异,以期在满足干涉条件的前提下增大了玻璃片厚度的测量范围。
实验原理与之前类似,只是此时式(1) 中 d'应为两光路中的玻璃片的厚度差,即:【2】
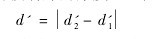
为便于操作,实验中令 d'2< d'1。这样,实验中加入玻璃片后要再次调出白光干涉只需让 M1镜向分束镜移动即可。优点是可以避免引入仪器空程差。
表 2 给出了在两光路中均插入不同厚度的石英玻璃片前后在视场中观察彩色条纹时 M1镜的位置及相应的位置变化。可以看出:在 M1镜光路中插入玻璃厚度达4. 2 mm 时,依然可以观察到白光干涉,而之前在 M1镜光路中插入玻璃厚度为3. 0 mm 时就几乎观察不到干涉现象了。这也验证了我们的观点,即插入的玻璃到一定厚度观察不到干涉条纹,主要是由于两路光相遇时光强相差过大导致的。由表 2 实验结果,我们还可以看出,改进后的实验方法可测量的玻璃厚度范围也拓宽了。此外,我们还计算了插入玻璃的折射率,见图 3。【图3.表2】
在完成上述实验内容的过程中,为提高实验的精确度,我们还总结出了以下实验调节技巧:
(1)试验中以白光干涉条纹中央的黑条纹作为起始参照量,使得试验中零光程差的要求更为严格;(2)尽量避免实验过程中因振动带来的仪器元件的移动,造成 d 的微小变化;(3)由于加入材料后,实验光程增大,所以操作时一定是沿 d 减小的方向来得到放入材料前后的两次白光干涉,以避免空程差的引入;(4)实验过程中,让一部分光不经过材料,可利用这部分光作为参照物,便于反复调节,也可以避免因拆装材料造成的仪器振动。
4 结 论
基于迈克尔逊干涉仪,通过在单一光路中及两光路中放置不同厚度的玻璃片,观察白光干涉现象并测量玻璃片的折射率。所购买的厚度为0. 5 mm、1. 0 mm、1. 2 mm、2. 0 mm 的石英玻璃的折射率略有差别,说明了材质的细微差异。在单一光路中插入玻璃片的厚度到 3. 0 mm 时干涉现象消失主要是因为两路光相遇时光强相差较大所引起的。我们设计的在两光路中均放置玻璃片拓宽了待测玻璃片的厚度测量范围。
参考文献:
[1] 高文琦,叶蓉华,何永蓉,等. 光学[M]. 南京:南京大学出版社,1994:96-101.
[2] 沈小峰,陈浩元. 物理学发展史概述[J]. 北京师范大学学报(自然科学版),1979(4):1-11.
[3] [4] 周 中. 探讨中的米的新定义[J]. 计量工作,1960(3):17-18.
[5] 徐文韬,李全伟,李吉骜,等. 用迈克耳孙干涉仪测量厚透明材料折射率[J]. 物理实验,2012,32(6):35-39.
[6] 蔡小镇,蒋晓龙,赵促飚. 探究汞灯测量透明薄片厚度的新方法[J]. 大学物理实验,2011,24(1):26-28.
[7] 万伟. 迈克尔逊干涉仪测透明介质厚层及折射率[J]. 大学物理实验,2013(2):21-24.
[8] 王军,等. 利用傅里叶变换和色度学原理分析白光干涉图的形成[J]. 大学物理实验,2013(1):17-20.Investigation of White Light Coherence by Adjusti





