
1、引言
在生物细胞检测领域,光学手段正发挥愈来愈重要的作用,其中,基于弹性散射光的光学检测方法可以在不引入外源介质的情况下,测量分析处于自然状态下的活细胞的内部结构分布及变化。和光强度角度分布探测方法相比,基于弹性散射光的测量方法具有光学系统简单,获取信号精度高等优势。其检测原理在于细胞内部的多种亚细胞器不仅呈颗粒状,而且具有与细胞质不同的折射率,因此能够使入射光产生弹性散射;通过测量入射激光在不同角度上的强度分布或某个固定角度上的光谱,即可完成细胞形态的检测。此外,综合这两种测量方式进行细胞检测的实验系统也已经问世。
目前,根据测量角度范围的不同,基于弹性散射光谱的颗粒尺寸精密测量可以分为几种典型方式:一种是在背向很小的一个角度范围内测量的背向弹性散射光谱测量;一种是在背向较大角度范围内测量的共聚焦背向弹性散射光谱测量;还有一种是在侧向较大角度范围内测量的暗场弹性散射光谱测量。后2种方式可以实现对单个球形颗粒的成像以及对其尺寸的超衍射极限分辨提取,但两者均对建立散射角积分计算模型提出了很高的要求。虽然第一种方式只能用于测量包含大数量球形颗粒的悬浮溶液,但却拥有散射理论模型简单、分析推断颗粒尺寸精度高的优点;而且通过寻求更为先进的光谱数据分析方法,该方式能够更为快速地获得球形颗粒混合溶液中的颗粒尺寸分布。
本文集中探讨了背向弹性散射光谱测量中获取光谱的不同实验方法及其优缺点,通过实验结果比较了目前普遍使用的光纤探头测量和透镜系统平行光入射及收集测量两种方法。本研究不仅能为实际应用中光谱获取方法提供参考依据,还可以为光谱获取方法的优化设计提供借鉴。
2、光谱获取及分析的基本原理
2.1微米颗粒的背向弹性散射光谱特性
在不考虑光吸收的情况下,微米球形颗粒的背向散射光谱呈现规则的周期起伏。对于折射率与周围介质相近的颗粒,这种特征可以由Ray-leigh-Gans近似公式来理解:
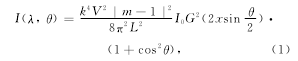
其中:L为测量距离,k=2π/λ,V为颗粒体积,m为颗粒的相对折射率(接近于1),I0为入射光强度,θ为散射角,G(u)=3(sin u-ucos u)/u3,x=ka定义为尺度参数,a为颗粒半径。当θ≈180°时,光谱的周期性主要来自于G(2x)。一般颗粒的周期性需要通过Mie散射数值计算结果进行解读。这种特征性周期光谱结构使得利用弹性散射光谱获得超衍射极限分辨的颗粒尺度信息成为可能。
然而,在实际的光谱获取及分析中,θ实际上仍然存在一个小范围Δθ的波动,而且平均散射角θ并不一定严格等于180°,它们会对光谱分析产生一定的影响。
对于较小的颗粒即亚微米量级的颗粒,这种影响可以忽略;但对于较大的颗粒即微米量级的颗粒,这种影响比较明显。由式(1)可以推断:函数G取决于x与sinθ2的乘积,当x较大时,因θ变化产生的影响会比较大;另外,这也可以从Mie散射数值计算来加以理解。
图1比较了两种尺度不同的聚苯乙烯微球颗粒在水溶液中其微分散射系数随角度变化的Mie散射计算结果(即散射强度随角度的变化)。这里入射波长为600nm,而聚苯乙烯和水的折射率按照各自的色散关系取值。从图中可以看到,在θ=180°附近,直径d=0.5μm颗粒的光强度变化较为平缓,而d=5μm颗粒的光强度变化较为明显。图中纵轴取对数坐标。因为不同波长的光散射强度会不同,所以颗粒越大,在θ=180°附近处的光谱变化会越明显。
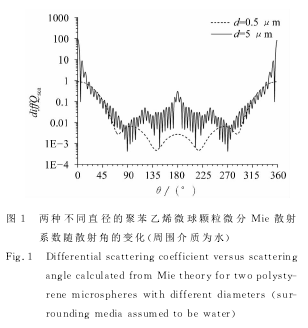
2.2基于光纤探头的光谱获取及分析
基于光纤探头的颗粒背向弹性散射光谱获取会因是否将光纤探头插入颗粒溶液中以及光纤探头的具体设计而有所不同。其基本原理如图2所示,测量系统由一根传输光纤和一根收集光纤构成。图中光纤探头在颗粒溶液之外,距离溶液面测量高度为h1,为了避免收集到来自溶液面的镜面反射光,两根光纤都沿垂直方向旋转了一个角度β(一般取~25°)。
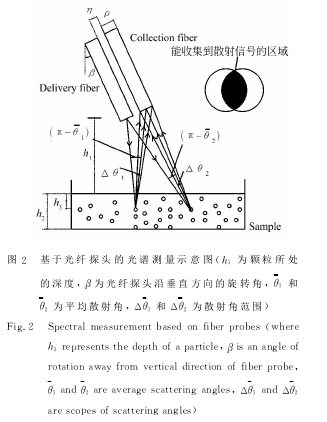
如图2中的插图所示,只有在两个光纤数值孔径(NA)重叠区域内的颗粒才能够被探测到。而颗粒的位置不同,其平均散射角(π-θ)(定义为两个光纤中心的张角)以及散射角范围Δθ(定义为每个光纤的张角)实际上也不同。但是,当:h2<<h1,h1>>(ρ+η), (2)(其中:h2代表溶液厚度,ρ和η分别代表光纤的直径以及光纤的间距)时,可近似认为所有颗粒的θ和Δθ相同,分别为:
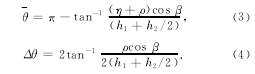
由于实际测量中收集到的光强度反比于(h1+h3)的平方(h3代表颗粒所处的深度),h1不能过大,否则会导致信噪比过低,因此难以达到式(2)的条件。此时,θ和Δθ的取值分布较为复杂,给光谱的计算分析带来了难度。
2.3基于透镜系统的光谱获取及分析
由于基于透镜系统的光谱获取方法采用平行光照明以及平行光收集,与光纤探头测量相比,散射角范围更加明确,光谱分析更为简明、准确。
图3为使用立方体分束器(BS)构成的光谱获取透镜系统。其中,透镜L1将入射光准直为平行光,透镜L2将背向散射的平行光会聚到收集光纤中。需要注意的是,不能将光纤探头直接耦合到一个透镜来实现准直和会聚功能,因为这样会使透镜表面的反射光进入到收集光纤中。
在图3所示的系统中,入射平行光经过分束器的90°反射后,沿平行于分束轴的方向照射到颗粒溶液。由传输光纤、透镜L1、BS、透镜L2、收集光纤构成的系统需要固定在一起,并沿垂直方向旋转一个小的角度(一般取~25°),以避免收集到颗粒溶液表面的反射光。另外,收集光纤还需偏离透镜L2光轴一个小的位移Δx,这是为了避免收集到分束器表面的反射光。
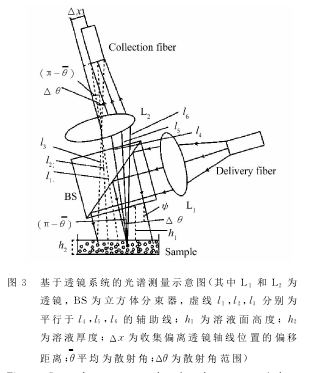
从图中虚线画出的光线平行线辅助线可以看出,进入收集光纤的背向散射光的平均散射角θ(定义为到达收集光纤中心的光线在进入透镜L2之前与分束器轴向的偏转角)为:
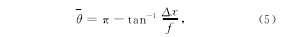
其中:f代表透镜L2的焦距。散射角范围Δθ(定义为到达收集光纤边缘的光线在进入透镜L2之前的夹角)为:
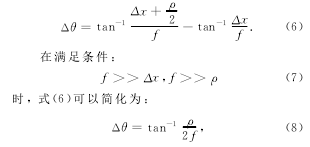
也就是说Δθ与Δx无关。比较式(5)与式(3)、式(8)与式(4)可知,相比于光纤探头系统,透镜系统的散射角不再受到溶液厚度、测量系统与颗粒溶液间距离的影响,而只由透镜L2的焦距以及收集光纤的偏离位移和直径决定。
3、实验结果及分析讨论
3.1实验样品
实验采用标准尺寸聚苯乙烯微球颗粒悬浮制品(PSN1005,纳微科技)稀释而成的颗粒悬浮溶液。该制品标明的颗粒直径的平均值为4.955μm,标准方差为0.156μm,初始质量浓度为1%。再将溶液稀释50倍使质量浓度为0.02%,在此浓度下用Mie散射数值计算可得入射光波长为550nm时,散射系数为μs=0.97cm-1。在光谱测量时,将这个稀释颗粒溶液搅拌均匀后,倒入底面直径为35mm的细胞培养皿(CORNING 430165)中,当倒入1mL颗粒溶液时,溶液厚度h2=1mm(见图2和图3)。在实验中厚度最大为h2=3mm,这时对应的光学厚度为τ=μsh2=0.291。在这种条件下,忽略颗粒多次散射对测量的影响,认为背向散射光等于各个颗粒的单次散射光的非相干叠加。
3.2光纤探头测量实验
在光纤探头光谱测量实验中(如图2所示),光纤探头(FCR-7UV200-2-ME,Avantes)由6根照明传输光纤紧密环绕1根收集光纤构成,光纤直径均为200μm,数值孔径NA均为0.22。光源采用脉冲氙灯(AvaLight-XE,Avantes),它耦合到一根600μm光纤的最大功率为180μW。
光谱仪为单通道光纤光谱仪 (AvaSpec-2048,Avantes),其测量光谱为300~900nm。本文分别取颗粒悬浮溶液厚度h2=1,2mm以及测量高度h1=3,6,9mm,共进行了6次实验,得到了在3种测量高度下漫反射白色参考瓦(WS-2,Avantes)的光谱,将其记为参考光谱信号Sref;还探测了相同h2条件下去离子水的光谱信号作为背景信号(记为Sbg)。最后,获得的颗粒背向散射信号为:
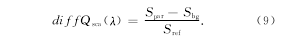
式(9)对应于理论中的微分散射系数。
表1列出了6次实验收集各个信号所用的光脉冲数。将这些光脉冲数进行归一化后代入式(9)中,计算结果如图4所示。
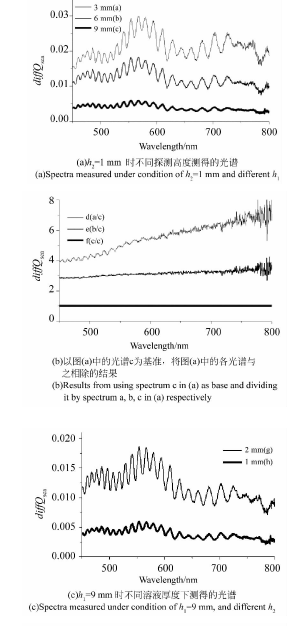
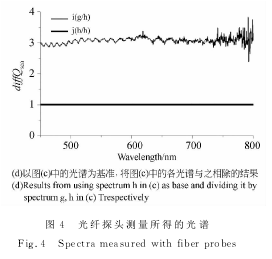
图4(a)给出了溶液厚度h2=1mm时,3个不同测量高度的光谱测量结果。为了比较这3个光谱是否因h1的改变而发生变化,图4(b)给出了这3个光谱分别除以h2=1mm、h1=9mm时光谱(即曲线c)的结果。很显然,最下面的f为一个数值恒等于1的直线。从图4(b)可以看到,虽然曲线e并没有明显偏离f;但曲线d明显地偏离f,其主要表现为随波长的增加而倾斜,而在短波长段仍然保留有图4(a)光谱中的周期起伏结构。这表明在测量高度h1有较大变化时,颗粒背向散射光谱不仅有因L而发生的整体改变,而且还有因散射角变化而产生的光谱形状变化。
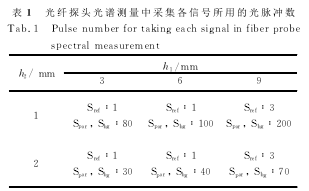
为了考察溶液厚度对光谱的影响,图4(c)给出了测量高度h1=9mm时,两种不同测量厚度的光谱测量结果。由图4(d)可知,曲线i在短波长段仍然有光谱周期起伏结构。因此,因溶液厚度引起的散射角变化对颗粒背向散射光谱测量有明显的影响,这与前文的理论分析相符。
3.3透镜系统测量实验
基于透镜的光谱测量系统如图3所示,实验选用的光源为强度可调的连续氙灯 (TunablePowerArcTM1000,OBB Corporation),两根光纤的直径均为ρ=400μm、数值孔径NA=0.22,实验测得从传输光纤出射的光功率为230μW。两个透镜的直径均为25.4mm、焦距f=35.0mm(AC254-035-A-ML,Thorlabs Inc.),立方体分束器为非偏振型,工作在可见光波段 (CMI-BS013,Thorlabs Inc.)。如图所示,设收集光纤偏离位移Δx=800μm。同样进行了6次实验,所测的颗粒悬浮溶液厚度h2分别为2,3mm,测量高度距离h1分别为9,12,15mm。表2列出了测量各个信号所用的积分时间,最后在用式(9)计算光谱时将所有的信号归一到1ms。
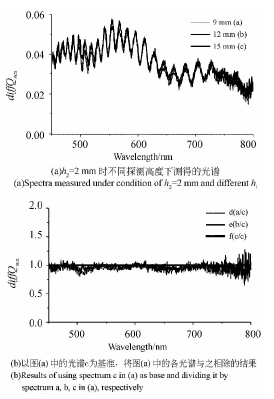
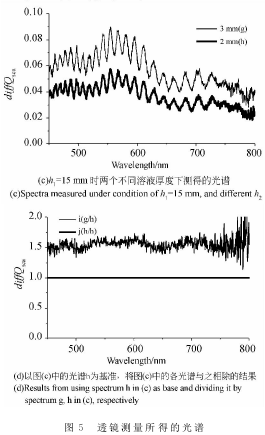
光谱计算结果如图5所示。从图5(a)和图5(b)容易看出,溶液厚度对光谱测量结果的影响很小,可以忽略。从图5(c)和图5(d)可以看到,测量高度变化对光谱形状也没有影响:其相除的结果在排除噪声外接近于一条平直线,在短波长段也没有出现光谱的周期起伏结构。这是因为测量高度不影响散射角(参见式(5)和式(8))。以上的实验结果也很好地符合本文的理论分析。
3.4两种方法测量光谱的Mie散射计算拟合
背向散射光谱测量的最终目的是获得微球颗粒的尺寸,包括平均直径以及直径的标准方差(假设为高斯分布),故需要建立一个Mie散射计算数据库,将测量光谱与各个尺寸的理论计算结果逐一比对,寻找到最佳的拟合结果。由于本文的目的不是为了研究这种尺寸的提取方法,因此这里采用生产厂家提供的颗粒尺寸值作为参考,给出了与测量光谱拟合最好的Mie散射计算结果。
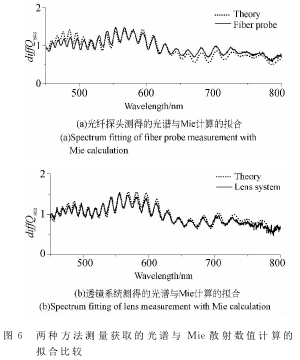
如图6所示,图6(a)和6(b)分别显示了光纤探头测量光谱(h2=2mm、h1=9mm)、透镜系统测量光谱(h2=2mm、h1=15mm)与理论计算的比较。
Mie散射计算所取的颗粒尺寸为平均值d=4.85μm、标准方差Δd=0.034μm,折射率的取值考虑了聚苯乙烯和水的色散,计算时散射角取单一的平均角。由图2和图3的几何关系计算得到,散射角分别为(π-0.022)和(π-0.023)(为了分析方便,没有对散射角度范围取积分计算)。图中的测量光谱和理论计算都做了归一化,取波长为625nm处的光谱为1。分别将图6(a)和图6(b)中的实验测量光谱和理论计算光谱进行互相关计算,得到的相关系数分别为0.93和0.96。由此可知,即使在光纤探头测量优化条件下,还是透镜系统测量光谱与理论拟合结果更相符。因此,选用透镜系统测量光谱再由数据库搜索方法能得到精度更高的颗粒尺寸结果。
3.5讨论
图4、图5、图6验证了理论分析结果,即透镜系统测量所获光谱对应的背向散射角有更好的定义,更有利于光谱的理论计算和颗粒尺寸分析。由于无法完全避免来自立方体内表面的反射光,因此透镜测量时背景信号所占的比例较大,同时也限制了光谱测量的积分时间。这个问题可以通过采用片状和楔状分束器来解决,但表面平行的片状分束器会带来由两表面的反射光相互干涉形成的光谱周期结构,从而干扰光谱分析;而两表面有小角度夹角的楔形片状分束器会使得光学系统的同轴调整变得复杂。
从另外一个方面来看,光纤探头测量不仅具有实验系统简单、易于操作的优点;而且当设置测量高度足够远、溶液厚度足够小的时候,背向散射角的定义也会变得更加明确,但这些设置也会导致信噪比的降低。光纤探头光谱测量的局限性在测量微米量级的颗粒时存在,但对亚微米颗粒的测量可以忽略。
4、结论
本文通过理论分析和实验验证,细致地比较了光纤探头测量和透镜系统测量这两种背向散射光谱获取方法的优缺点。实验结果表明,在提取微米球形颗粒尺寸时,前一种方法简便易行,但所获得的光谱形状会受到测量高度以及颗粒溶液厚度的影响;后一种方法中不存在这些问题,但其光谱测量的信噪比较低。因此,在颗粒尺寸提取精度要求不高的情况下,可以选用光纤探头测量方法;在精度要求高时,应选用透镜测量方法,同时采用滤波去噪声信号处理的手段来提高颗粒尺寸的提取精度。下一步研究将集中于如何提高透镜系统光谱测量的信噪比,一种可能的途径是用反射凹面镜来取代透镜,这样可以在系统中避免使用光分束器,在提高信噪比的同时保留透镜系统测量的优点。





