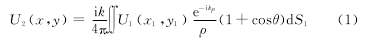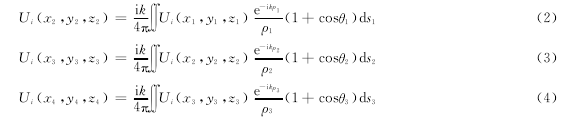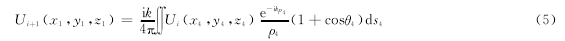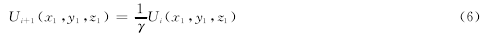谐振腔是激光器系统的一个最基本的元件,决定了光束的质量。激光器产生的光束的聚焦特性和传输特性与激光谐振腔的光场模式密切相关。因此,激光谐振腔光场模式的计算对激光器的设计有着重要的意义,而腔镜倾斜与面型误差是直接影响激光谐振腔系统性能的两个重要因素,文献[1]计算了腔镜变形对平凹稳腔激光振荡模式的影响,张增宝等人研究了腔镜失调与面型误差对氧碘化学激光器折叠虚共焦非稳腔光场的影响。近年,高斯反射镜及其倾斜对谐振腔的影响也被广泛研究。但上述工作主要是针对驻波腔激光器进行的研究。环形激光器主要应用在高精度的角度测量中,高精度的应用决定了其对光束质量的高要求。袁杰等人利用光学矩阵的方法研究了角度和轴向移动扰动引起的环形腔光线的位置和角度误差,但该方法利用的是几何光学理论,无法计算与物理光学有关的参量。因此,为提高光束质量和改进调腔方法,本文利用物理光学软件研究腔镜倾斜对平面环形腔振荡模式的影响。
1 Fox-Li迭代法
谐振腔的分析计算方法主要有传输线理论分析法、场理论分析法、迭代法、微扰法、时域有限差分法以及有限元法等。Fox-Li迭代法虽然比较繁琐,但却具有普遍的适用性,它可以用来模拟激光在谐振腔中的渡越过程,原则上能够计算任何几何形状的开腔中的自再现模。GLAD软件的建模思想就是应用Fox-Li迭代法。它使用复数的振幅来描述波前,并对光束的整个传输路径做衍射模型,可以处理光学系统设计中无法忽略的衍射效应。
将菲涅耳-基尔霍夫衍射积分公式应用于平面环形谐振腔,表达式为
式中:
U1(x1,y1)为镜S1上的场分布;U2(x,y)为U1(x1,y1)经腔内一次渡越在镜S2上生成的场;ρ为镜面上点 (x1,y1)到点 (x,y)的距离;θ为ρ与点 (x1,y1)法线的夹角;k为波数。
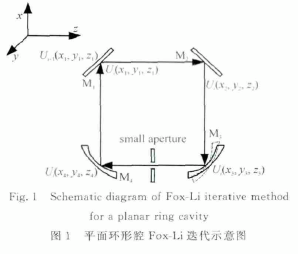
建立如图1所示坐标系,在第i次循环中,镜片M1的光场为Ui(x1,y1,z1),由式(1)可得镜片M2的光场Ui(x2,y2,z2)、镜片M3的光场Ui(x3,y3,z3)及镜片M4的光场Ui(x4,y4,z4)分别为
第i+1次循环中,镜片M1的光场Ui+1(x1,y1,z1)为
用式(2)~(5)进行多次循环,当满足
时,光波在腔内实现自再现,Ui(x1,y1,z1),Ui(x2,y2,z2),Ui(x3,y3,z3),Ui(x4,y4,z4)分别为自再现模在镜M1,M2,M3,M4处的光场分布。以上各式中ρ1为镜M1上点 (x1,y1,z1)到镜M2上点 (x2,y2,z2)的距离,θ1为ρ1与镜M1上点 (x1,y1,z1)处法线的夹角,ρ2为镜M2上点 (x2,y2,z2)到镜M3上点 (x3,y3,z3)的距离,θ2为ρ2与镜M2上点 (x2,y2,z2)处法线的夹角,ρ3为镜M3上点 (x3,y3,z3)到镜M4上点 (x4,y4,z4)的距离,θ3为ρ3与镜M3上点 (x3,y3,z3)处法线的夹角,ρ4为镜M4上点 (x4,y4,z4)到镜M1上点 (x1,y1,z1)的距离,θ4为ρ4与镜M4上点 (x4,y4,z4)处法线的夹角,γ为复常数。
2结果与分析
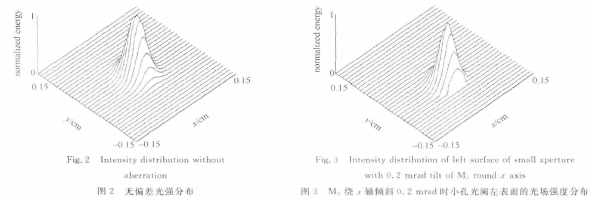
设置谐振腔参数:M1和M2为平面镜,M3和M4为球面镜,曲率半径为8m。各镜面半径均为5mm,各边腔长8.4cm,小孔光阑半径0.7mm,波长632.8nm。用GLAD软件对上述谐振腔进行建模,初始光场设置为平面波。对于顺时针光,理想情况下小孔光阑左表面的光强分布如图2所示。
GLAD软件是将偏差通过命令直接加在光束波振面上,所以下文所给偏差均指镜面偏差对光束波振面的影响偏差大小。一般来说,镜面各点偏差是光束波振面对应点偏差的0.5倍。
本文只考虑镜面M3偏差的影响,同时只考虑顺时针光束。对于逆时针光,在偏差不大的情况下,M3镜面偏差对其影响与对顺时针光束影响基本相同。镜面倾斜分为绕x轴倾斜和绕y轴倾斜,正方向符合右手定则,倾斜大小由镜面偏离理想位置的角度大小定义。
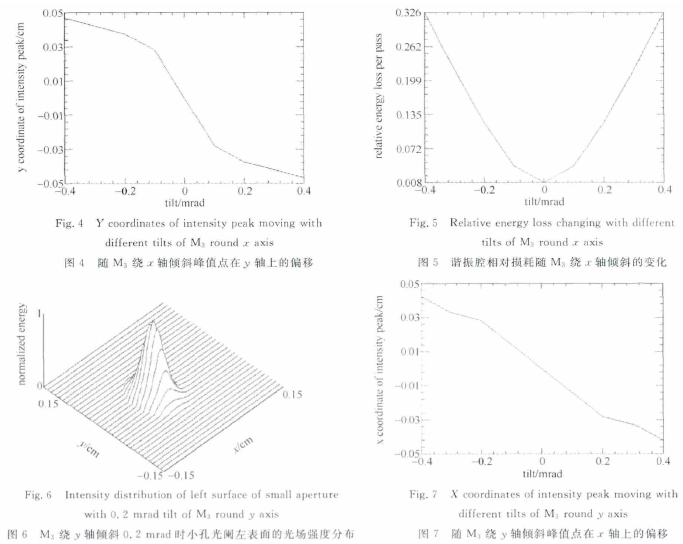
图3给出镜M3绕x轴倾斜0.2mrad时,小孔光阑左表面的光场强度分布。倾斜为-0.2mrad情况下的光场强度分布与倾斜为0.2mrad情况下的光场强度分布关于y=0平面对称。与图2对比可以看出镜M3绕x轴倾斜时,光强峰值点在y轴方向上向镜面边沿偏移,光场偏离理想高斯基模。图4和图5分别定量给出光强峰值点和谐振腔损耗随倾斜的变化。从图4和图5中可以看出随着镜M3绕x轴倾斜增加,光强峰值点在y轴方向上向镜面边沿偏移增加,腔损耗增大。
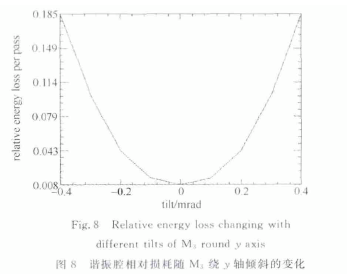
图6给出镜M3绕y轴倾斜0.2mrad时,小孔光阑左表面的光场强度分布。倾斜为-0.2mrad情况下的光场强度分布与倾斜为0.2mrad情况下的光场强度分布关于x=0平面对称。光强峰值点和谐振腔损耗随倾斜大小的变化分别如图7和图8所示。从图中可以看出随着镜M3绕y轴倾斜增加,光强峰值点在x轴方向上向镜面边沿偏移增加,腔损耗增大。
对比两组倾斜偏差仿真结果可知,在相同倾斜偏差下,镜M3绕x轴倾斜偏差对光场的影响要比绕y轴倾斜偏差对光场的影响大。由于在环形激光器中一圈的增益系数小于0.03,因此倾斜大小要控制在0.1mrad之内,即镜面倾斜要在10″以内。
3结论
本文用GLAD软件对平面环形腔进行建模,仿真计算了镜面倾斜条件下的光场分布、光场峰值点偏移及谐振腔损耗。结果表明:在相同倾斜偏差下,镜M3绕x轴倾斜偏差对光场的影响要比绕y轴倾斜偏差对光场的影响大;随着镜面倾斜的增加,光场峰值点向镜面边沿偏移增加,光束质量变差,腔损耗增大;为了获得较理想的基模高斯光场,镜面倾斜要控制在10″以内。
参考文献:
[1] 库耕,程祖海,朱松林,等.腔镜变形对平凹稳腔激光振荡模式影响的数值研究[J].强激光与粒子束,1997,9(3):447-450.(Ku Geng,Cheng Zuhai,Zhu Songlin,et al.Numerical study of effect of the mirror distortion on the oscillatory mode variation of stable resonator.High Power Laser and Particle Beams,1997,9(3):447-450)
[2] 张增宝,金玉奇,桑凤亭,等.腔镜失调与面型误差对光束质量影响的研究[J].强激光与粒子束,2005,17(4):491-494.(Zhang Zengbao,Jin Yuqi,Sang Fengting,et al.Beam quality investigation on misalignment and surface-shape error of cavity mirror.High Power Laser andParticle Beams,2005,17(4):491-494)
[3] 彭玉峰,李阔湖,陈靖,等.高斯反射镜及其倾斜对平凹腔激光场分布的影响[J].强激光与粒子束,2006,18(3):
385-388.(Peng Yufeng,Li Kuohu,Chen Jing,et al.Influence of Gaussian reflectivity mirror and its tilt on the laser field distribution of plano-ncave resonator.HighPower Laser and Particle Beams,2006,18(3):385-388)
[4] 范泛,杨克成,张波,等.高斯镜平凸非稳腔本征模场的有限元数值计算[J].激光技术,2007,31(2):192-195.(Fan Fan,Yang Kecheng,Zhang Bo,et al.Numerical calculation of mode-fields of the spherical plano-convex unstable resonator with Gaussian reflectivity mirror bymeans of the finite element method.Laser Technology,2007,31(2):192-195)
[5]Yuan Jie,Long Xingwu,Chen Meixiong.Generalized ray matrix for spherical mirror reflection and its application in square ring resonatorsand monolithic triaxial ring resonators[J].Optics Express,2011,19(7):6762-6776.
[6]Yuan Jie,Chen Meixiong,Long Xingwu,et al.Beam position controlling method for 3Doptical system and its application in non-planar ringresonators[J].Optics Express,2012,20(17):19563-19579.
[7] 于得利,桑凤亭,金玉奇,等.氧碘化学激光输出光斑漂移和变形研究[J].强激光与粒子束,2001,13(2):151-154.(Yu Deli,SangFengting,Jin Yuqi,et al.Study of the drift and deformation for COIL output beam spot.High Power Laser and Particle Beams,2001,13(2):151-154)
[8] 许杰田,张猛,李杰,等.基于矢量有限元法的微波谐振腔高频特性研究[J].电子技术,2010,23(10):59-61.(Xu Jietian,Zhang Meng,Li Jie,et al.High-frequency characteristics of resonance cavity based on the vector finite element method.Electronic Science and Technolo-gy,2010,23(10) 59-61)[9] 李源,战可涛.激光谐振腔光场及远场分布的数值模拟系统[J].北京化工大学学报:自然科学版,2012,39(1)106-110.(Li Yuan,ZhanKetao.Numerical simulation system of the optical field and the far field distribution of a laser resonator.Journal of Beijing University ofChemical Technology:Natural Science,2012,39(1):106-110)
[10]周炳琨,高以智,陈倜嵘,等.激光原理[M].6版.北京:国防工业出版社,2009:41-50.(Zhou Bingkun,Gao Yizhi,Chen Tirong,et al.Principles of lasers.6th ed.Beijing:National Defense Industry Press,2009:41-50)
[11]汪之国,龙兴武,王飞,等.激光陀螺本征模偏振态与磁敏感特性的理论研究[J].物理学报,2013,62:054205.(Wang Zhiguo,LongXingwu,Wang Fei,et al.Theoretical analysis ofpolarization eigenstate and magnetic sensitivity in a ring laser gyro.Acta Physica Sinica,2013,62:054205)