
电力需求量是电力工业进行生产与建设的基础,也是电力系统进行规划与设计的基础,它将决定着电力工业的发展水平、发展速度、技术方向与能源结构情况,同时决定着输变电工程的规划、布局、装机容量以及电网结构的情况. 因此,对电力需求量与经济增长之间的关系进行动态效应分析,将具有重要的理论意义与应用价值.
本文基于向量自回归模型、脉冲响应函数和方差分解等方法对电力需求量进行科学分析和评价,对我国电力需求量与经济增长水平进行动态效应分析,为我国制定电力需求量发展战略提供依据,具有一定的参考价值和现实意义.
1 相关文献综述
随着科学技术的进步和发展,20世纪中期学者们开始研究电力需求的理论,但是由于受到电力系统自身规模等因素的限制,电力需求的研究一直没有成型的体系.
20世纪80年代以来,电力需求的理论研究开始兴起,并且由于电力自身的重要性和特殊性,各个国家都非常重视对电力需求的研究,在研究过程中,已经发展了多种方法,如时间序列分析法、灰色预测法、神经网络法、组合模型和协整检验模型等.Asafu-Adjaye[1](2000)运用误差修正模型和协整检验模型探讨了亚洲四个发展中国家电力需求与GDP之间的因果关系,研究表明在短期内泰国和菲律宾存在电力需求与GDP之间的双向因果关系,印度存在电力需求到GDP的单向因果关系;在长期过程中,泰国和菲律宾的电力需求、GDP和价格之间互为因果关系,印度的电力需求和价格均是GDP的原因.
Thoma[2](2004)根据美国1973-2000年的月度数据,按照不同部门分别实证检验了电力需求与经济产出之间的因果关系,结果显示经济发展对总电力需求的变化有明显的Granger因果关系. 刘畅、高铁梅[3](2011)利用月度数据,构建了误差修正模型,研究了影响电力需求的长期经济因素与短期动态调整效应,研究发现工业经济增长、经济结构重型化和库存均是影响电力需求的重要因素. 黄建[4](2012)基于LEAP模型能源需求模块的基本思路,对我国电力需求进行了情景分析和预测. 李新英[5](2012)运用格兰杰因果关系和误差修正模型研究了新疆地区电力需求与国内生产总值以及三次产业增长之间的关系及其影响程度,并在此基础上对新疆未来一段时间的电力需求量进行了预测.
2 变量选取和数据处理
由需求理论可知,经济增长是电力需求的主要影响因素,经济增长可以采用我国国内生产总值来衡量.本文选取的变量有:电力需求(全社会用电量)ED和国内生产总值GDP. 为了消除数据的异方差性和波动性,所选变量均取对数,所选数据来自于我国统计年鉴和能源统计年鉴,样本区间是1990-2012年.
3 变量平稳性检验
为了防止在模型中出现伪回归的问题,需要对所选变量进行平稳性检验. 本文采用ADF检验法对所选变量进行平稳性检验,检验结果如表1所示.
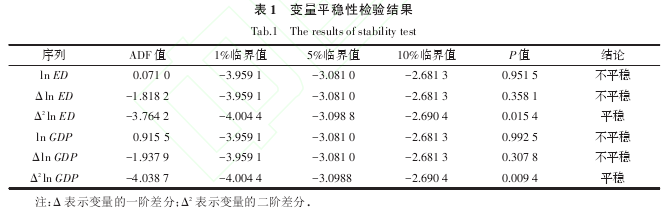
由表1检验结果可以看出,变量ln ED、ln GDP的水平值和一阶差分值均存在单位根,属于非平稳序列;二阶差分值在5%水平下显着,属于平稳序列. 因此,ln ED和ln GDP是I(2)序列.
4 向量自回归估计
在上述平稳性检验的基础上,构建了ln ED与ln GDP之间的向量自回归模型,如表2所示.
由表2可以看出,变量ln ED与ln GDP的向量自回归模型R2分别为0.996 6、0.998 5,接近于1;调整的R2分别为0.995 3、0.998 0,接近于1,这说明模型的拟合程度很好.
F统计值分别为748.321 5、1 773.820,均通过1%水平下的显着性检验.
AIC值分别为-3.578 4、-3.932 6,SC值分别为-3.342 4、-3.696 6,两者均符合向量自回归模型的要求.
电力需求受自身一阶滞后项显着正向影响,二阶滞后项显着负向影响;经济增长(国内生产总值)受自身一阶滞后项显着正向影响,二阶滞后项影响不显着. 经济增长(国内生产总值)滞后一阶和滞后二阶均对电力需求有显着正向影响,且随着时间的推移,影响效应递减;同样,电力需求滞后一阶和滞后二阶均对经济增长(国内生产总值)有显着正向影响,且随着时间的推移,影响效应递减.

5 脉冲响应函数分析
根据向量自回归模型中的脉冲响应函数,对电力需求量和国内生产总值进行冲击效应实证检验,结果如图1和图2所示,其中实线用来说明脉冲响应函数程度,虚线用来说明上下90%区间的偏离程度.
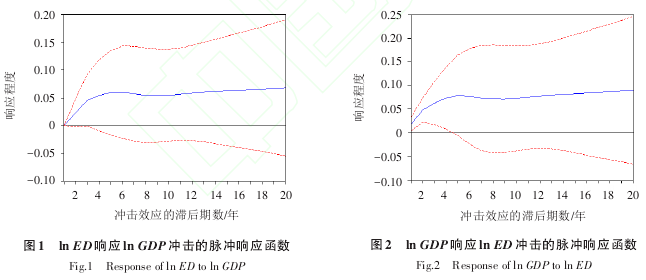
由图1可知,在1~4期,国内生产总值对电力需求量的冲击效应从0开始迅速上升,在第5期达到最大值,约为6%,随后几期略有下降,其后逐渐达到稳定,在5%水平下处于稳定状态.
由图2可知,在1~4期,电力需求量对国内生产总值的冲击效应迅速上升,在第5期达到最大值,约为8%,在随后的6~10期,呈下降趋势,在11期之后逐渐上升并趋于平稳,在9%水平下达到稳定状态.
6 方差分解
方差分解是通过分析每一个结构冲击对内生变量变化的贡献度,进一步评价不同结构冲击的重要性.因此,方差分解给出对VAR模型中的变量产生影响的每个随机扰动的相对重要性的信息[6]. 本文给出了电力需求量滞后30期的方差分解结果,如表3所示.
由表3可以看出,电力需求在前7期下降速度很快,由100%下降到53%,随后逐渐平稳下降,最终稳定在48%水平上.
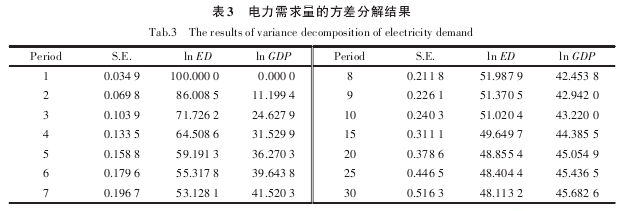
在滞后1期,国内生产总值对电力需求变化的冲击贡献率水平为0,随后开始上升,在滞后2期到滞后7期,由11.20%快速上升到41.52%,随后平稳上升,最终稳定在45.6%的水平上.
由此可知,经济增长对电力需求量的冲击效应贡献率水平是非常高的.
7 研究结论
本文通过向量自回归模型、脉冲响应函数和方差分解等方法对电力需求进行实证分析和研究,得出了如下研究结论.
1)根据ADF单位根检验可知,ln ED和ln GDP是I(2)序列.
2)电力需求受自身一阶滞后项显着正向影响,二阶滞后项显着负向影响;经济增长(国内生产总值)受自身一阶滞后项显着正向影响,二阶滞后项影响不显着. 经济增长(国内生产总值)滞后一阶和滞后二阶均对电力需求有显着正向影响,且随着时间的推移,影响效应递减;电力需求滞后一阶和滞后二阶均对经济增长(国内生产总值)有显着正向影响,且随着时间的推移,影响效应递减.
3)国内生产总值对电力需求量的冲击效应在5%水平下处于稳定状态;电力需求量对国内生产总值的冲击效应在9%水平下达到稳定状态.
4)在电力需求的冲击效应贡献率水平上,经济增长(国内生产总值)的贡献率水平高达45.6%的水平.
在上述实证研究的基础上,本文提出如下政策建议:要重视电力需求量的分析,建立有效的电力短缺预警体系;调整产业结构和经济结构,改变经济发展模式;提高科学技术水平,改善工业用电效率;大力发展环保产业,促进可再生资源的发展.
参考文献:
[1]Asafu-Adjaye J. The relationship between energy consumption energy prices and economic growth:time series evidence fromAsian developing countries[J]. Energy Economics,2000(22):615-625.
[2]Thoma M. Electrical energy usage over the business cycle[J]. Energy Economics,2004(26):463-485.
[3] 刘 畅,高铁梅.中国电力行业周期波动特征及电力需求影响因素分析--基于景气分析及误差修正模型的研究[J].资源科学,2011(1):169-177.
[4] 黄 建.基于LEAP的中国电力需求情景及其不确定性分析[J].资源科学,2012(11):2124-2132.
[5] 李新英.基于ECM模型的新疆电力需求预测[J].新疆财经,2012(1):61-66.
[6] 高铁梅.计量经济分析方法与建模:Eviews应用及案例[M]. 2版.北京:清华大学出版社,2009.





