
财务困境 (Financial Distress)又称 “ 财务危机 (FinancialCrisis)、 财务失败 (Financial Failure)”, 财务破产 (FinancialBankruptcy)只是财务困境的一种极端表现,是最严重的财务困境状态。企业因财务困境导致破产实际上是一种违约行为,所以财务困境又可称为“违约风险(Default Risk)” (吴世农和卢贤义,2001)。自 Beaver(1966)使用财务比率来预测企业失败的研究以来,有关企业财务困境预测的研究便成为国内外学者广泛关注的课题。当前,预测和管理企业财务困境越来越成为企业经营、投资决策和贷款决策的一个重要组成部分(Beaver,Correin& McNichols,2011),股东、债权人以及企业员工都对财务困境或即将破产的风险给予高度的重视。
目前,理论界关于企业财务困境预测的研究基本形成了以下三种主流的方法或模型:基于会计信息的传统模型,以Altman (1968) 的 Z- Score 模型为代表;基于未定权益分析(Contingent Claims Analysis,CCA)的模型,该模型视权益为公司资产价值的一项看张期权,如 Vassalou & Xing(2004)的研究;风险模型(Hazard model),这种模型同时使用会计和市场数据来预测企业的财务困境,以Shumway(2001)的研究为代表。这些模型的判别能力常通过以下3 个维度来衡量(Agarwal & Taffler,2014):区分失败和非失败企业的能力;不同模型捕获企业失败或破产的增量信息程度;当失败和非失败企业的误分类成本不同时,模型的绩效表现。
现有研究常在这3个维度间进行比较,并得出了一些有争议的结论。
一、基于会计信息的传统模型
基于会计信息的传统模型从上市公司公开披露的财务报表中滤取信息来评估企业陷入财务困境的程度。学术界普遍认为Beaver(1966)是最早使用财务指标来预测企业失败的研究者,实际上,早在1932 年,Fitzpartrick 就在 《注册会计师》 杂志上发表了《A Comparison of Ratios of Successful Industrial Enterpriseswith Those of Failed Firms》 一文,该文运用单个财务指标对 19家上市公司的财务状况进行预测,并发现净利润/ 股东权益、股东权益/ 负债这两个财务指标的判别能力最高。这是最早使用单变量分析法的文献,只是该文的学术性不及Beaver(1966)& Altman(1968)的研究。1966 年,Beaver 使用配对样本建立了一个单变量判别分析模型并使用二分法的分类技术,研究发现“现金流/总负债”是预测企业失败的最佳变量,其预测失败的精度可达企业失败前5 年。
在Beaver 研究的基础上,Altman(1968)使用多元判别分析技术(MDA),建立了 Z- Score 模型:Z=0.012X1+0.014X2+0.033X3+0.006X4+0.999X5,其中X1=(流动资产 - 流动负债) / 总资产,反映营运资本占总资产的比例,它可以衡量企业全部资产的流动性水平;X2= 留存收益 / 总资产,反映企业总资产中留存收益的数额;X3= 息税前收益 /总资产,是企业财务失败最有利的依据之一;X4= 股东权益的市场价值 /负债总额的账面价值,反映企业的财务结构;X5= 销售收入 / 总资产,反映企业运用资产以产生销售收入的能力。Altman 发现模型中的 5 个比率要明显优于Beaver 的现金流与总负债比,且根据这一模型,企业破产的状况能在其真正进入破产的前 2 年准确地预测出来。此外,他还指出 Z- Score 模型不仅能用于上市公司的破产预测,而且在商业贷款评估、企业内控评估及投资标准评估中都有实用价值。
由于 Z- Score 模型是针对制造业上市公司所建立的,Altman,Haldeman & Narayanan(1977)又以制造业和零售业公司为样本,通过迭代程序,建立了一个 7 变量的 ZETA 模型,扩展了Z- Score 模型的应用。只是因涉及未公开的资料,我们无法得知这 7 个变量的判别系数。鉴于实践中有些学者对 Z值模型提出的异议,Altman(2000)又公开发表了 《Predicting FinancialDistress of Companies: Revisiting the Z- Score and ZETA Models》一文,对 Z- Score 模型作了重新检验和修订,使之能够应用于私人企业和非制造业上市公司。
多年来,很多有关企业财务困境的研究都是基于 Altman(1968)的 Z- Score 模型进行的,直到 80 年代,Altman 所使用的MDA 技术的使用率才有所下降(Dimitras,Zanakis & Zopounidis,1996),但它仍是一个被普遍接受的标准方法,从而在学术研究中作为一种基准方法(Baseline Method)而被频繁使用(Altman &Narayanan,1997)。 80 年代, MDA 开始被一些定性反应模型(Qualitative- response Model)所替代。如 Ohlson(1980)开创了 Logit方法在企业失败预测应用中的先河,Zmijewski(1984)则最早将Probit分析方法用用于企业财务困境预测中,Duffie,Saita &Wang(2007)称这是第二代实证研究,Balcaen & Ooghe(2006)对这些研究作了很好的综述和归纳。
尽管这类模型被广泛使用,却由于其缺乏理论基础而备受批评。Hillegeist,Keating & Cram等(2004),指出由于会计报表本质上是历史性的,是基于持续经营假设制定的,用他们来预测未来,尤其是当涉及违反持续经营假设时,存在着根本性的缺陷,其实用性是有限的。Agarwal & Taffler(2008)指出,由于比率及其权重都是通过对样本的分析获得的,这类模型会视样本情况而有所不同。而且,财务报表的一些固有特性也使得这类模型的有效性受到质疑:会计报表表达的是一个公司过去的业绩,可能无法及时地预测失败;稳健性原则和历史成本会计意味着企业真实的资产价值可能不同于所记录的账面价值;会计数据易遭受盈余管理。此外,还有一些与建模有关的方法论问题。如 Zmijewski(1984)指出,这类模型是有偏的,因为在建模的过程中失败的企业常被过度抽样。Hillegeist,Keating & Cram等(2004)指出了这类模型的两个计量问题:其一,样本选择性偏误,这来自于模型对每一个破产公司只使用一个、非随机挑选的观测值;其二,无法模拟基准破产风险 (这种风险能导致对数据的横截面依赖) 的时间变化趋势。Shumway(2001)证实了这些问题能导致有偏的、非有效的、不一致的参数估计。Beck,Katz & Tucker(1998)也指出标准误会被低估。因此,随着时间的推移,为了保持模型的实用性,定期重建模型是很必要的(Mensah,1984; Hillegeist,Keating & Cram 等,2004)。
二、基于未定权益的模型
鉴于上述缺陷,近年来一些学者开始采用基于未定权益分析的方法来预测企业的财务困境。这类模型基于 Black &Scholes(1973)和 Merton(1974)的期权定价理论,将权益视为公司资产价值的一种或有要求权,企业即将失败或破产的可能性是期权在到期日毫无价值的概率。模型所需要的数据从资本市场获取,迄今为止,最有影响力的这类模型当属Moody's KMV 模型。Agarwal &Taffler(2014)指出,这类模型克服了基于会计信息的传统模型的一些根本缺陷:①它为公司破产提供了一个可靠的理论模型,因为他们是基于 BSM模型而建立的;②在有效市场上,证券价格不仅能反映所有包含在会计报表中的信息,而且还能显示会计报表以外的信息;③市场变量不大可能受会计政策的影响;④市场价格反映了企业未来期望的现金流,因此更适用于预测的目的;⑤这类模型输出的结果不依赖时间和具体的样本。正因为如此,这类模型得到一些学者的大力推崇。
Vassalou & Xing(2004)采用这类模型来计算单个公司每月的违约概率,发现这种违约风险的度量确实能够预测企业实际的违约,模型中的资产波动性指标提供了有关公司违约可能性的重要信息。Hillegeist,Keating & Cram 等(2004)使用相对信息量检验方法比较了基于市场的BSM 模型和各种基于会计的积分模型预测企业破产的绩效表现。结果发现,相比各种基于会计信息的传统模型,基于市场的BSM 模型提供了明显较多的关于破产概率的信息。他们建议后续的研究应该使用 BSM模型来预测企业的破产可能性,因为它是破产概率强有力的代表指标。Reisz &Perlich(2004)的实证研究发现,尽管Z- Score模型在一年内的预企业财务困境预测研究的国际进展及启示测效果要优于 KMV- Merton 模型和计算更为精密的敲出期权(Down- and- out Options)模型,但从长远来看,基于未定权益的模型要更好一些。Duffie、Saita & Wang(2007)指出,在一段时间内的违约概率模型中,Merton DD概率有重要的预测能力,它能产生一系列期限结构违约概率。
由于Merton模型中公司价值及其波动性是不可直接观测的,一些学者便围绕着这两个变量的估计对模型作了一些修订和扩展,如Bharath & Shumway(2008)建立了一种简化式的Merton 模型,并证明了 Merton 模型的函数形式的重要性。 随 后 Charitou, Dionysiou &Lambertides 等(2013)采用一种更直接的简化方法来估计公司价值的波动性,扩展和泛化了 Bharath & Shumway(2008)的研究,并证明了从这种直接的波动性估计方法中所得出的模型预测效果更好。
然而,Agarwal & Taffler(2008) and Beauer & Agarwal(2014)指出,使用未定权益框架来预测破产也不是那么简单易行的:首先,它需要一系列的前提假设。Saunders & Allen(2002)指出,它需要证券收益的正态性假设;而且它无法区分不同类型的债务,因假定所有的公司都只有一个单一的零息债券。其次,Avramou,Chordia & Jostova 等(2010)指出,陷入困境的公司很容易遭受市场微观结构问题,如市场交投清淡和限制卖空,从长远来看,这会导致价格远离公允价值。最后,这类模型所需要的一些关键变量都是不可直接观测的,如资产的波动性、期望的资产收益率以及资产的市场价值等,这一点至关重要。因此,对于这类模型的实证结果目前是没有定论的。如 Kealhofer& Kurbat(2001)指出,Merton 模型在预测违约方面普遍地优于Moody's KMV 模型和基于会计指标的模型;Merton 模型已经包括了评级与会计指标中的信息。但是 Altman(2002)却得出了相反的结论,认为基于会计信息的 Z- Score 模型的违约预测要优于 Merton 模型。Campbell,Hilscher & Szilagvi(2008)的研究指出在缺乏市场杠杆和波动性信息的情况下,除了其他的协变量,基于Merton 模型的违约距离几乎没有增加额外的信息。
Bharath & Shumway(2008)也证实 Merton DD 模型所给出的违约概率对于预测违约并不是一个充分的统计量。
三、风险模型
上述两类模型之间的争相辩论,促使现有研究主张合并这两种模型的信息来源以预测企业的财务困境。McQuown(1993)指出,财务报告反映公司的理事情况,市场价格更能反映公司发展的未来趋势,最准确的违约度量方法应该同时使用这两种数据资源。Sloan(1996)发现市场价格不能精确地反映公司账户的信息,因此会计数据能够补充市场数据。Beaver,McNichols& Rhie(2005)指出市场价格反映了丰富而全面的信息组合,其将财务报表数据作为一个子集而纳入其中。
因此,Pope(2010)主张合并会计和财务这两个学科,Christidis & Gregory(2010)也指出合并会计数据和市场价格的信息有助于克服会计信息的时效性问题。根据这些争议,最新的风险模型(Hazard Models)拆除了会计和市场数据之间的严格区分,合并利用了这两种来源的信息。
风险模型,同二元 logit 模型密切相关,也被学者称为“多周期(Multi- period)logit 模型”。它有着类似于 logit 模型的函数形式,如下:
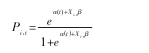
此模型在以下两个方面不同于普通的logit模型:第一,下标t表达了对每一个公司i,它使用多个公司年观测值;第二,它包含了时变的基准风险率(Baseline Hazard Rate), α (t)。
Shumway(2001)对此有详细的说明和介绍,并通过理论推导证明了多周期logit 模型也即离散时间风险模型,指出风险模型能够产生一致的并在多数情况下还是无偏的估计量。Hillegeist,Keating & Cram 等(2004)称风险模型特别适用于分析那些由二元的、时间序列以及横截面观测值所组成的数据,如破产数据。
风险模型同时使用会计和市场数据来预测企业的困境状况。
目前,使用风险模型来预测企业财务困境已成为国外学者普遍采用的一种方法,Duffie,Saita & Wang(2007)称这是最新一代的建模研究。由于使用了样本公司整个生命周期内的数据,模型的实证表现都相当的好。如 Shumway(2001)比较研究了风险模型和基于会计信息的传统模型的绩效,结果发现,那些来自于Altman 的 Z- Score 模型和 Zmijewski 的 Probit 模型的会计变量有一半在统计上不显著,与企业的失败没有明显的关系。他还进一步指出,会计和市场变量的组合明显提高了模型的预测精度。
Charalambakis,Espenlauby & Garrett(2009)采用英国证券市场的数据进行检验,也得出了类似的结果。Chava &Jarrow(2004)采用扩展的数据库,遵循 Shumway 的方法,重新估计了 Shumway的风险模型,再次证明了风险模型的优越性。Campbell,Hilscher & Szilagyi(2008)比较了风险模型和基于市场信息的未定权益模型。他们发现,在信息量检测中,风险模型不仅要优于Mood's KMV 模型,而且还囊括了未定权益模型中几乎所有的与破产相关的信息。由于所建立的模型有较高的 Pseudo- R2,他们声称比Shumway(2001)模型的绩效表现还要好 。 Christidis &Gregory(2010)展示了一个类似于 Campbell, Hilscher & Szilagyi(2008)的风险模型,并且声称在英国证券市场上,当考虑宏观经济和会计变量时,风险模型的表现更好。
在上述所有研究的基础上,Bauer & Agarwal(2014)展开了一项综合研究,使用 ROC 曲线、相对信息量检验以及模型经济价值检验比较了三类模型的实证表现,三类模型分别使用了Shumway (2001) and Campbell,Hilscher & Szilagyi(2008)的风险模型、Taffler(1983)建立的 UK- based Z- Score 模型和 Bharath &Shumway(2008)的未定权益模型。经过实证分析得出以下重要结论:首先,就违约概率而言,所有模型都能区分出失败和非失败的公司。
不过,Z- Score模型和基于未定权益的模型都是有校准误差的,而风险模型的平均违约概率很接近于实际的违约率。
其次,ROC 曲线分析显示, Shumway(2001) and Campbell et al(2008)的风险模型没有明显的差别,但都明显优于其他两类模型;再次,相对信息量检测发现,所有的模型都承载了与企业财务困境有关的信息。风险模型中没有包含的信息,其他两类模型中也没有。而与 ROC 曲线分析相反,Z- Score 模型比未定权益模型承载了更多关于企业后续失败的信息。
最后,不同模型的经济价值比较显示,在竞争的市场中,两个风险模型的经济效用远优于Z- Score模型和未定权益模型;相比较Campbell,Hilscher & Szilagyi(2008)的风险 模型,Shumway(2001)的模型带来了更高的市场份额和利润、更高的信用程度和更高的风险加权资产收益率。
总之,在所有3个绩效维度上,风险模型要优于预测破产的其他两类模型,而且Shumway(2001)的模型要更好。
四、国际研究的启示
目前,在现有数据的基础上选择最佳的预测模型仍是个实际的挑战。Galindo & Tamayo(2000)指出,最佳的评判模型需要具备以下5 个必要条件:准确性。模型假设导致的错误率要低;简约性。解释变量不宜过多;非平凡性。得出结果有意义;可行性。在一个合理的时间范围内进行,并使用实际的数据来源;透明和可解释性。提供有关数据关系的高水平见解,以及理解模型的结果从何而来。上述国际建模研究基本上都在这5 个条件之列。由于国内资本市场起步较晚,相关研究相对滞后。虽然理论界对企业财务困境预测研究已做出了不少贡献,但与国际研究的成熟性相比,仍处于初步探索阶段。
纵观国际研究的理论和实证过程,至少为我们推进国内企业财务困境的研究提供了以下启示:
1.企业财务困境预测仍是学术研究的一个重要主题一个预测模型的效果如何,在很大程度上取决于可利用的信息。伴随着企业实践的发展以及企业所处的环境状况的变动,在预测企业发生财务困境与否时,理论研究所关注的信息逐渐由静态向动态扩展,由微观向宏观过渡。动态地看待企业财务困境并试图建立动态预测模型,已是相关研究的主流方向,有着重要的理论和实践价值。
2.同时使用市场和会计信息来预测企业财务困境已成为一种趋势这就意味着越来越多的建模研究将会跳出只依赖于会计信息的框架,资本市场的信息和宏观经济环境状况将越来越受到重视。合并利用这些信息将会提供相对精确的判断,至于如何将这些信息合并在一起,基于持续期分析的风险模型是一个不错的选择。
3.鉴于1和2,可知预测因子已越来越多,但模型中的变量并不是越多越好这就要求所选的变量要少而精,要有足够的代表性,既能够说明问题,又相互补充。Shumway(2001)的风险模型,只有 5个变量,包括 2 个会计变量和 3 个市场变量。文章发现,后来的相关研究基本上都使用了这3个市场变量,只在会计变量的选择上略作一些更改和替换。会计变量名目众多,但也无外乎以下几个方面:盈利性、流动性、现金流以及杠杆等,在度量杠杆时,基本上都使用了资产负债率,其他的变量也多是有影响力的现有文献中所采用的。
4.实证研究的样本要足够大,数据要足够多文章发现国外的研究,其样本跨度有40年之久,且有使用月度数据、季度数据的样本观测值能高达几万个。中国证券市场收录的统计数据多是从1998年开始的,至今也不足20年的历史,而学者们也多用年度数据来进行实证研究,因此可以考虑扩展样本期间,用季度数据或月度市场表现来考量。
5.在模型精确度的比较中,仅用分类正确率以及类别间均值差异的比较是不够的Sobehatr & Keenan(2002)提出了一套验证模型有效性的技术方法,即使用累计准确度(Cumulative Accuracy Profiles,CAP)、准确率(Accuracy Ratios,AR)、 条件信息平均比例 (ConditionalInformation Entropy Ratios,CIER) 和共有信息平均值 (MutualInformation Entropy,MIE)四个量化指标来衡量模型的准确性,后被学者们广泛采纳。Stein(2005)、Blochlinger & Leippold(2006)的研究框架,也可为我们提供有益的借鉴和参考。
参考文献:
[1] Beaver W H,Correia M,McNichols M. Financial statement analysis andthe prediction of financial distress [M].Now Publishers Inc,2011.
[2] Vassalou M,Xing Y. Default risk in equity returns [J].The journal offinance,2004,59(2):831- 868.
[3] Bauer J,Agarwal V. Are hazard models superior to traditional bankruptcyprediction approaches? A comprehensive test [J].Journal of Banking &Finance,2014,40:432- 442.
[4] Altman E I. Predicting financial distress of companies:revisitingthe Z- sco- re and ZETA models [J].Stern School of Business,New York University,2000: 9- 12.





