
引言
在资金投资过程中,理性的投资者都会考虑如何将持有的一定数量资本,在若干种含有风险的证券上进行合理的资金分配,以达到尽可能多地分散风险,并且获得最大的收益的目的。而对于这种证券组合投资决策问题,美国经济学家 Harry Markowitz于 1952 年首次提出了投资组合理论,利用均值 -方差模型进行了解释。目前,国内外的很多学者针对投资组合问题进行了比较深入的研究,并且取得了一定的有价值的成果.然而,针对制约资金投资的两个最主要的因素,即投资风险和投资收益,如何综合衡量这两个指标,并做出合理的组合投资决策,这也就引出了一个多目标投资组合的问题。而该问题属于复杂的非线性规划问题,传统的算法很难进行有效求解,因此,本文提出利用群智能优化算法 - 人工鱼群算法求解多目标投资组合问题,并取得了较好的效果。
1 多目标投资组合问题及其模型
假设市场上有 n 种资产 Si( i = 1,…,n) 可供投资者选择,现有数额为 M 的资金用作一个时期的投资,在这一投资时期内购买 Si的平均收益率为 ri,预期风险损失率为 qi,投资过程中存在一定的风险,考虑用 n 种资产中最大的一个风险度量总体风险。假设购买某种资产时要支付一定的交易费,设购买 Si支付的交易费率为 pi,当购买额不超过给定值 ui时,交易费按 ui计算; 另外,假设存入银行的存款利率为定值。建立如下多目标投资组合模型.设购买资产 Si的资金占总量 M 的比重为 xi,则所需交易费用为:【1】

2 人工鱼群算法的原理
人工鱼群算法( AFSA,Artificial Fish - school Al-gorithm) 是由李晓磊博士于 2002 年提出的一种新型的群智能优化算法.它的基本思想是,在一片水域中,鱼生存数目最多的地方一般就是本水域富含营养物质最多的地方。该算法就是根据这一特点,模仿鱼群的觅食、聚群、追尾以及随机行为,从而实现全局寻优。
2.1人工鱼个体相关定义
人工鱼个体状态可表示为向量 X = ( x1,x2,…,xn) ,其中 xi( i =1,2,…,n) 为欲寻优的变量; 人工鱼当前所在位置的食物浓度表示为 Y = f( X) ; 人工鱼个体之间的距离表示为 dij= | | Xi- Xj| | ; 人工鱼每次觅食的最大试探次数为 trynumber,人工鱼感知距离为 visual,人工鱼的最大移动步长为 step,以及拥挤度因子为 δ。
2.2 人工鱼行为描述
2.2.1 觅食行为 设人工鱼当前状态为 Xi,在其感知范围内( visual) 随机选择一个状态 Xj,如果该状态的食物浓度优于其当前状态时,则人工鱼向该方向前进一步; 反之,重新随机选择状态 Xj,判断是否满足前进条件。反复尝试 trynumber 次后,若仍不满足条件,则随机移动一步。
2.2.2 聚群行为 设人工鱼当前状态为 Xi,探索当前领域内( dij< visual) 的伙伴数目 nf及其中心位置Xc,如果 Ycnf< δYi,则表明该中心位置的食物浓度优于当前状态且不太拥挤,则人工鱼向该 Xc位置前进一步,否则执行觅食行为。
2.2.3 追尾行为 设人工鱼当前状态为 Xi,探索当前领域内状态最优的伙伴 Xmax,如果 Ymaxnf < δYi,则表明该伙伴位置的食物浓度优于当前状态且其周围不太拥挤,则人工鱼向该 Xmax位置前进一步,否则执行觅食行为。
2.2.4 随机行为 该行为的实现比较简单,是觅食行为的缺省行为。
2.2.5 公告板 用来记录最优人工鱼个体的状态。
每个人工鱼在寻优过程中,都会将自身状态与公告板的进行比较,若自身状态较优,则更新公告板的状态为自身状态,这样公告板上记录的就是历史最优的状态。
3 基于AFSA 算法的多目标投资组合问题
3.1 模型的优化
对于本文所述的多目标投资组合问题的求解,可用下述方式首先转化为单目标问题,然后再进行求解: 设置权值 ρ 为投资净收益总额的权重,那么 1- ρ 为总体投资风险权重( 0≤ρ≤1) ,那么上述多目标投资组合模型转化为单目标模型为:【2】
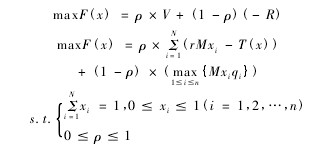
对于模型中 ρ 的取值,投资者可以根据自身情况进行适当的调整,以得到适当的投资组合决策。
3. 2 模型的求解步骤利用 AFSA 算法求解多目标投资组合问题的步骤描述如下:
Step1: 初始化人工鱼群规模,随机生成 N 条人工鱼,并设定算法中所需的参数,人工鱼移动的最大试探次数 trynumber、人工鱼感知范围 visual、人工鱼移动步长 step、拥挤度因子 δ,以及执行算法的最大迭代次数。
Step2: 根据多目标投资组合问题的数学模型设定算法的食物浓度函数。
Step3: 计算初始各人工鱼个体当前状态的食物浓度,并取最优个体的状态记录到公告板。
Step4: 各人工鱼分别进行觅食、聚群和追尾操作,选择最优的行为移动,更新自身状态。
Step5: 更新后,各人工鱼将自身状态与公告板的进行比较,若优于公告板,则更新公告板的状态。
Step6: 算法终止条件的判断。若满足迭代终止条件,则输出计算结果; 否则转入 Step4 继续执行。
4 仿真实验
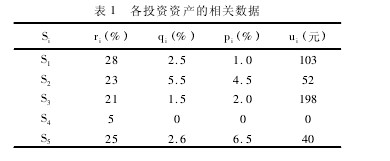
为了验证人工鱼群算法的有效性及优越性,本文使用 MATLAB 编程,应用 AFSA 算法和遗传算法( GA) 分别进行仿真实验,根据所得结果进行比较研究。现有五种投资资产可供选择,设投资总金额 M为 1000 元,各个资产的收益率、风险损失率等数据见表 1 所示。
人工鱼群算法的参数设置为鱼群规模为 50,最大迭代次数为 100,感知范围 visual =2. 5,移动步长step = 0. 4,拥挤因子 δ = 0. 618,以及试探次数 try-number = 100; 用 MATLAB 编程,取不同 ρ 值得到不同风险偏好情况下的资金投资组合,见表 2 所示。
从表 2 可以看出,对于多目标投资组合问题,在不同风险偏好的情况下,人工鱼群算法都能够得到较好的资金投资组合方案。该仿真实验结果表明了AFSA 算法对求解此类问题的有效、可行性。
对人工鱼群算法的参数设置不变,用于比较的GA 算法的最大迭代次数 N = 100,交叉概率为 0. 8,变异概率为 0. 01,群体规模 P = 100; 运算结果的投资组合方案对比见表 3( 设 ρ =0. 5) .【表1.2.3】
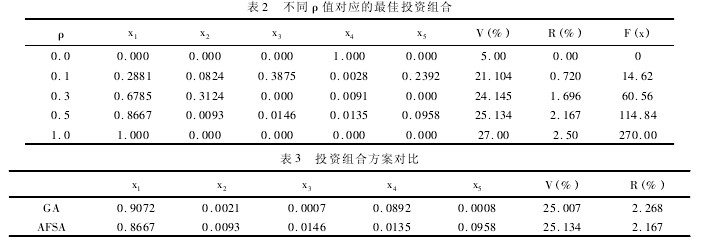
从表 3 可以明显看出,对五种资产进行投资,相对于 GA 算法而言,人工鱼群算法能获得更好的投资组合决策方案,使得投资收益尽可能大,而风险尽量小,表明了该算法在求解多目标投资组合问题上的高效性以及优越性。
5 结论
本文提出基于人工鱼群算法对多目标投资组合问题进行了研究及应用,通过使用 MATLAB 编程,并取得了较好的效果。实验表明该算法解决此类问题非常有效,但是人工鱼群算法作为一种新型的智能优化算法,仍有一些不足之处,因此对求解此类问题在资产数目较多、投资资金量较大时的性能,仍有待今后进一步的研究和改进。
参考文献:
[1] H. MARKOWITZ. Portfolio selection[J]. Journal of Fi-nance,1953,7: 77 - 91.
[2] Kendall G,Rollins S. Advanced project portfolio manage-ment and the PMO[M]. Florida: J Ross Publishing,2003.
[3] 哈里。马科威茨。 资产组合选择和资本市场的均值[M]. 上海: 上海人民出版社,1999.
[4] 胡日东。组合证券投资优化模型的比较研究 [J]. 运筹与管理,2001,10( 1) : 99 -103.
[5] 万丽英,李兴斯,张新芬。 证券投资组合一种多目标优化模型及其算法 [J]. 数学的实践与认识,2010,40( 24) : 9 -14.
[6] 朱德通。最优化模型与实验[M]. 上海: 同济大学出版社,2003.
[7] 李晓磊。一种新型的智能优化方法_人工鱼群算法[D]. 杭州: 浙江大学,2003.
[8] 王冬冬,周永权。人工鱼群算法在求解非线性方程组中的应用[J]. 计算机应用研究,2007,24(6) : 242 -244.
[9] 张汉强,卢建刚,陈金水。新的混合智能优化算法及其多目标优化应用[J]. 计算机应用,2010,30(5):1290 -1292.





