在 Hawking 证明黑洞具有热辐射之前,Beken-stein 等人就发现,若将黑洞的表面引力和视界面积类比于温度和熵时,黑洞力学四定律与普通热力学四定律将非常类似。但是 Hawking 认为这只是形式上的类似,因为黑洞不能被看作普通的热力学系统,不能简单的用普通热力学定律来描述。自从Bekenstein 和 Hawking 分别证明黑洞的熵与其视界面积成正比之后,黑洞熵的统计起源成为几十年来人们研究的一个热点。
为了对黑洞统计熵给出一个满意的解释,各种探求黑洞统计熵的方法应运而生。其中用的最多的是 1993 年诺贝尔物理学奖获得者 G ′t Hooft 提出的 brick-wall 模型,用此方法得到了各种时空背景下的黑洞标量场和 Dirac 场的统计性质,发现黑洞熵就是其外部量子场的熵,从而通过计算外部量子场的状态数,并选取合适的截断因子,能得到与黑洞视界面积成正比的 Bekenstein-Hawking(B-H)熵。 同时为了避免在视界附近的态密度发散以及计算方便,在计算中不得不引入人为截断因子和采用小质量近似。 近年来有学者对 brick-wall 模型进行了改进,提出了黑洞熵的主要贡献者是黑洞视界外的薄层场的熵。用此改进的方法克服了红外截断和人为引入,但是对紫外截断仍无法克服。
我们通过引入广义测不准关系对态密度的修正而计算黑洞的统计熵,很自然的避免了人为引入截断以及小质量近似。将广义测不准关系引入到黑洞量子统计熵的计算,是基于研究黑洞量子统计熵,确切的说是研究黑洞的量子效应,此时研究黑洞的辐射粒子或吸收粒子则必须考虑测不准关系。我们知道,当考虑引力作用时海森堡测不准关系不再满足,取而代之的是广义测不准关系。同样我们将此方法推广到对称的 dilatonic 黑洞不是微不足道,其意义在于检验将广义测不准关系引入量子统计熵计算的正确与否,另外对此方法是否可以避免人为截断进行确认。
本文的安排如下:正文第一部分,将利用广义测不准关系对态密度的修正对球对称 dilatonic 黑洞的量子统计的玻色场熵进行计算,在计算中所取的积分区间为从黑洞的视界面到无穷远观测者,测得的具有相同固有辐射温度的超曲面。且两曲面的固有厚度具有广义测不准关系的最小长度量级。正文第二部分,我们用同样的方法来计算费米场中的量子统计熵。最后给出总结与结论。在本文中取C = 攸 =G = KB= 1。
1、 球对称 dilatonic 黑洞
球对称 dilatonic 黑洞线元:
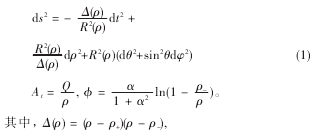

由文献知,无穷远静止观测者,测得的固有辐射温度为

由上式可得玻色场的熵为

在上式中应用了粒子的能量、动量和质量的关系ω2蛐 λ2= p2+ m2, m 是粒子的静止质量。(11) 式对 ρ的积分在视界附近。 而在视界附近-gtt(ρ+)→0, 于是(11)式可化为

时空为球对称时,无穷远静止观者,测得黑洞视界外任意 R(R > r+)上的固有辐射温度是相同的。所以对于时空为球对称黑洞,在计算黑洞视界附近的量子统计熵时,取的积分区间是[r+, R = r++ ε],其中为一正的小量。换句话说,所取的积分区间是从黑洞的视界到无穷远静止观这,测得黑洞视界外具有相同辐射温度的超曲面。由(4)和(5)式,我们知道在视界外,当 R 满足

时,无穷远观者,观测到的固有辐射温度是相同的。r+是黑洞视界位置,满足 gtt′ (r+) = 0。在视界附近gtt′ (r) ≈ (gtt′)′(r+)(r - r+)。由度规(1)知, 最小长度为:

则玻色熵的级数表达式(19)中的主导项与视界面积成正比且系数为 1 蛐 4,满足 B-H 熵。对黑洞熵修正值的探讨是当前研究的热点之一,人们利用各种方法来研究对黑洞熵的修正, 结果与其在量级上是一致的,且级数收敛。
2、 费米场的熵

由此, 我们可得黑洞视界附近费米场对应的熵为




则费米熵的级数表达式中的主导项与视界面积成正比, 满足 B-H 熵。
3、 总结
在本文中,利用广义测不准关系对态密度的修正,计算了黑洞视界附近玻色场与费米场的量子统计熵。 在没有人为引入截断和小质量近似的情况下,得到了黑洞统计熵的级数表达式。我们发现,当广义测不准关系中引入的无量纲常数 λ 满足(20)或(24)式时,黑洞量子统计熵级数表达式中的主导项与视界面积成正比,且满足 B-H 熵。通过我们的计算同时知道在球对称的 dilatonic 黑洞中,无量纲常数 λ 的值是与黑洞度规的 dilatonic 系数有关的。 计算结果表明,黑洞 B-H 熵与视界面积成正比这一定理,是与引力背景没有关系的,是普适的。另外,通过利用态密度修正的量子统计的方法计算球对称 dilatonic 黑洞 B-H 熵,克服了求解波动方程的困难,又提出对球对称时空计算黑洞熵的积分区间为:黑洞视界面与无穷远观测者测得视界外附近具有相同固有辐射温度的超曲面。





