摘 要: 介绍了暗能量宇宙学相关课题研究的一些最新的研究进展.作者多年来一直致力于暗能量问题的研究, 近年来在暗能量相关课题方面开展了大量的研究工作, 在若干方向取得了一系列有意义的进展.对这些课题研究的进展进行了简要介绍, 主要内容包括:暗能量宇宙学模型的观测限制研究, 暗能量与暗物质耦合参数的宇宙学测量, 在宇宙学中称重中微子与搜寻惰性中微子的研究, 遗迹中微子在银河系中的引力结团研究, 利用引力波观测开展宇宙学参数估计的研究, 暴胀宇宙学模型的观测限制研究.
关键词: 暗能量; 宇宙加速膨胀; 相互作用暗能量; 中微子质量; 引力波;
Abstract: This paper introduces the latest research progress of dark energy cosmology.The author has been devoted to dark energy research for many years.In recent years, a lot of research work has been carried out on dark energy-related topics, and a series of significant progress has been made in several directions.In this paper we briefly describe the progress of the research area, and the main contents include:observational constraints on dark energy models, cosmological measurement of the coupling parameter between dark energy and dark matter, weighing neutrinos in cosmology and searching for sterile neutrinos, gravitational clustering of relic neutrinos in the Milky Way, cosmological parameter estimation with gravitational wave observations, observational constraints on inflation models.
Keyword: dark energy; cosmic acceleration; interacting dark energy; neutrino mass; gravitational waves;
0、 引言
暗能量问题一直是宇宙学的核心课题之一.为解释宇宙当前的加速膨胀现象, 人们提出在当前的宇宙中大约70%左右的能量成分是由所谓的“暗能量”来提供的.暗能量最奇异的性质是它具有负压强, 或者说, 它所产生的万有引力是排斥性的, 因此如果暗能量在宇宙中占据主导地位, 它产生的排斥性的引力就会驱动宇宙加速膨胀.目前我们对暗能量的本质属性还不清楚.首先, 我们并不确切知道暗能量到底是什么.它是否宇宙学常数, 亦或是某种具有动力学机制的物理场?它如何影响宇宙的命运?其次, 我们不清楚暗能量与暗物质之间是否存在某种直接的相互作用.如果这种相互作用存在, 它如何影响宇宙的演化?第三, 我们并不确切知道爱因斯坦的广义相对论是否在整个宇宙的尺度上都是正确的.在宇宙尺度上修改引力可以得到某种有效暗能量, 在原则上得到与存在暗能量相一致的宇宙膨胀历史, 那么宇宙加速膨胀到底是由存在暗能量引起的还是由修改引力引起的呢?
目前, 利用宇宙学观测数据 (包括宇宙微波背景辐射、超新星、重子声波振荡等) 来确定暗能量的状态方程参数w是暗能量研究中最为关键的一步.结合普朗克卫星任务的观测数据和其他天文观测数据已经可以把w的精确度确定在约4% 的水平上 (在假定w为常数时) [1], 但是目前的精度仍不足以确定暗能量的性质以及区分不同的暗能量模型.未来的观测项目 (DESI、LSST、Euclid、WFIRST等) 致力于将w限制在好于1%的程度, 有望明确暗能量的本质属性.本文作者多年来一直致力于暗能量问题的研究.近年来, 作者所带领的团队在暗能量相关课题方面开展了大量的研究工作, 在若干方向取得了一系列有意义的进展.本文将简要介绍近年来在暗能量宇宙学相关的课题研究方面所取得的研究进展.实际上, 本文是作者主持的国家自然科学基金优秀青年科学基金项目 (项目号:11522540) 研究成果的一个总结.

1、 暗能量宇宙学模型的观测限制研究
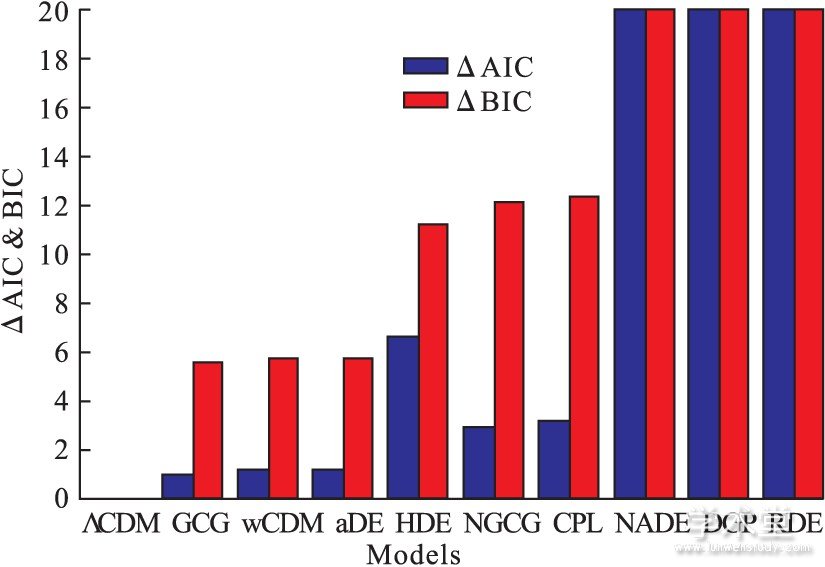
暗能量模型的比较研究.当前的宇宙学观测数据, 特别是在普朗克卫星任务释放最新的宇宙微波背景观测数据之后, 倾向于支持一个6参数基本ΛCDM模型[2].但是, 我们很难相信仅利用6个参数就可以全面地刻画宇宙的演化.因此这个基本模型必然需要在一些方面进行扩展, 比如在中微子质量、再电离历史、原初引力波、暗能量、暗物质等方面.未来的更加精确的观测数据应该可以对这些扩展模型进行精确检验.目前, 尽管ΛCDM模型比较被观测数据所支持, 但仍然有一些动力学暗能量模型也可以很好地拟合观测数据, 如果仅用卡方统计作为比较手段, 一些动力学暗能量模型在解释观测方面表现得比ΛCDM模型还要好.对于一些最流行的暗能量模型进行一个比较研究是非常有意义的.这样的研究可以告诉我们哪些暗能量模型可以很好地解释观测数据, 而哪些暗能量模型已经不被观测所支持.我们开展了这项暗能量模型比较的研究[3], 根据拟合当前观测数据的能力, 我们对10个典型且流行的暗能量模型进行了比较.我们利用的观测数据包括Ia型超新星的JLA样本、普朗克2015宇宙微波背景观测距离信息、重子声学振荡测量、哈勃常数直接测量等.由于不同的模型具有不同数目的参数个数, 为进行公平比较, 我们利用两种信息判据来评估这些模型的价值.我们的分析结果显示 (图1) , 根据解释观测的能力, 宇宙学常数模型仍然是所有暗能量模型中最好的模型;推广的恰普利金气体模型、常数w模型、α暗能量模型相较于宇宙学常数模型来说还是要差一些, 但仍可以非常好地解释观测数据, 是除宇宙学常数模型之外最好的暗能量模型;全息暗能量模型、新推广的恰普利金气体模型、CPL模型仍可以相当好地拟合当前的观测, 但是从一个经济可行的角度来说, 它们已不是那么好了;新年刻暗能量模型、DGP模型、里奇暗能量模型已经明显被当前观测数据排除了.
图1 暗能量模型的比较。取自Y.-Y. Xu & X. Zhang, Eur. Phys. J. C 76 (2016) 588
利用哈勃参数观测数据限制暗能量的研究.利用宇宙膨胀的几何测量对暗能量参数进行限制的方法是暗能量研究的最主要方法, 其核心是利用距离-红移关系来确定宇宙膨胀历史, 进而限制暗能量模型参数空间.然而, 哈勃膨胀率与暗能量状态方程参数之间是通过一个积分关系相联系的, 而距离与哈勃膨胀率之间也通过一个积分关系相联系, 因而距离与暗能量状态方程参数间存在两个积分关系.这导致通过距离-红移关系来确定暗能量状态方程参数非常困难.如果能够直接测量不同红移处的哈勃参数, 则可以更好地确定暗能量的状态方程参数, 因为二者之间只存在一个积分关系.对暗能量观测限制来说, 另一个问题是缺少高红移数据.当前的观测数据都集中在低红移处, 而高红移数据对打破暗能量模型参数之间的某种重要简并是非常关键的.一个重要的未来观测计划是测量高红移天体 (类星体) 的红移漂移.这个红移漂移测量是通过测量中性氢气体云的Lyman-alpha吸收线来完成的, 被称为Sandage-Loeb检验.欧洲南方天文台正在建设的欧洲极大望远镜 (E-ELT) 专门设计了一个CODEX项目, 就是用来测量红移漂移效应的.我们在一系列工作中按照CODEX的设计指标模拟了未来红移漂移数据, 对暗能量限制进行了预研[4,5,6,7].特色是利用动力学暗能量模型作为模拟数据的基准模型, 利用当前的观测数据来限制基准动力学暗能量模型, 得到的参数值用来产生模拟的未来红移漂移数据.这样做的好处是可以消除未来数据与当前数据间的不一致.我们在论文中[4,5,6,7]已讨论了多个一般的暗能量模型的参数限制, 表明未来的红移漂移数据对于打破当前重要的参数简并至关重要.不仅如此, 我们还模拟了未来的其他几何测量数据.基于空间暗能量探测计划“联合暗能量任务” (模拟了该项目的超新星和重子声学振荡数据) 的研究, 表明在未来结合距离测量与红移漂移测量对于限制暗能量状态方程参数是极其重要的.在这些工作的基础上, 我们进一步推进了该方面的研究, 讨论了包含未来红移漂移观测的哈勃参数测量对暗能量的限制[8].对于当前的哈勃参数测量, 我们考虑了31个数据点, 覆盖的红移范围从0.07到2.34.而利用未来的红移漂移观测也可以直接测量更高红移处的哈勃参数, 可覆盖的红移范围从2到5.因此, 我们讨论了红移漂移观测可以在利用哈勃参数测量限制暗能量性质的研究中发挥什么样的作用.我们以一些典型的暗能量模型为例来开展了这项研究, 考虑的暗能量模型包括ΛCDM模型、wCDM模型、CPL模型、全息暗能量模型.我们的结果显示, 仅利用一个10年的红移漂移观测即可在很大程度上改进利用哈勃参数测量对暗能量的限制.进一步考虑结合未来E-ELT和WFIRST哈勃参数观测的分析, 见文献[9].
2、 暗能量与暗物质耦合参数的宇宙学测量
在暗能量的本质属性的探索中, 有两点尤为重要:1) 暗能量是否有动力学, 理论上如何解释, 以及对宇宙的命运有何影响;2) 暗能量与暗物质之间是否存在某种直接的微妙相互作用, 其对宇宙学观测有何影响, 以及如何进行探测.暗能量与暗物质的直接耦合既会修改宇宙的膨胀历史, 也会对宇宙的结构增长历史带来影响, 因此对这种相互作用的探测要求我们必须从宇宙的膨胀历史和结构增长两个方面很好地理解相互作用暗能量模型.然而, 一旦我们在相互作用暗能量模型中计算宇宙学扰动, 我们就会发现, 在很多情况下 (对应于参数空间中的某些部分) 宇宙学扰动 (从早期的超视界尺度开始) 会发散, 这对于相互作用暗能量宇宙学来说是一个严重的灾难性问题[10].多年来, 人们面对这个问题只能采取避开这些带来发散的参数空间的办法, 只寻求探索一部分参数空间.扰动不稳定性问题说明我们其实根本不懂得如何考虑暗能量的扰动.由于不清楚声波如何在暗能量流体中传播, 为计算暗能量的压强扰动, 只能人为地为暗能量设定一个静系声速, 这导致在暗能量的压强扰动中包含非绝热模式 (相互作用项出现在该部分中) , 在某些情况下会引起扰动发散.我们在2014年针对该问题提出一个行之有效的解决方案, 建立起一个适合相互作用暗能量的参数化后弗里德曼理论框架 (PPF) , 基于暗能量的已知基本事实来有效地计算暗能量的扰动[11,12].在相互作用暗能量的PPF方案中, 扰动不稳定性被彻底消除 (图2) , 因此我们此后即可以利用观测数据来探索相互作用暗能量模型的完整的参数空间 (图3) [13,14,15,16,17,18].
图2 相互作用暗能量模型 (Q正比于暗物质密度的情况) 在尺度k = 0.1 Mpc-1的密度扰动演化。
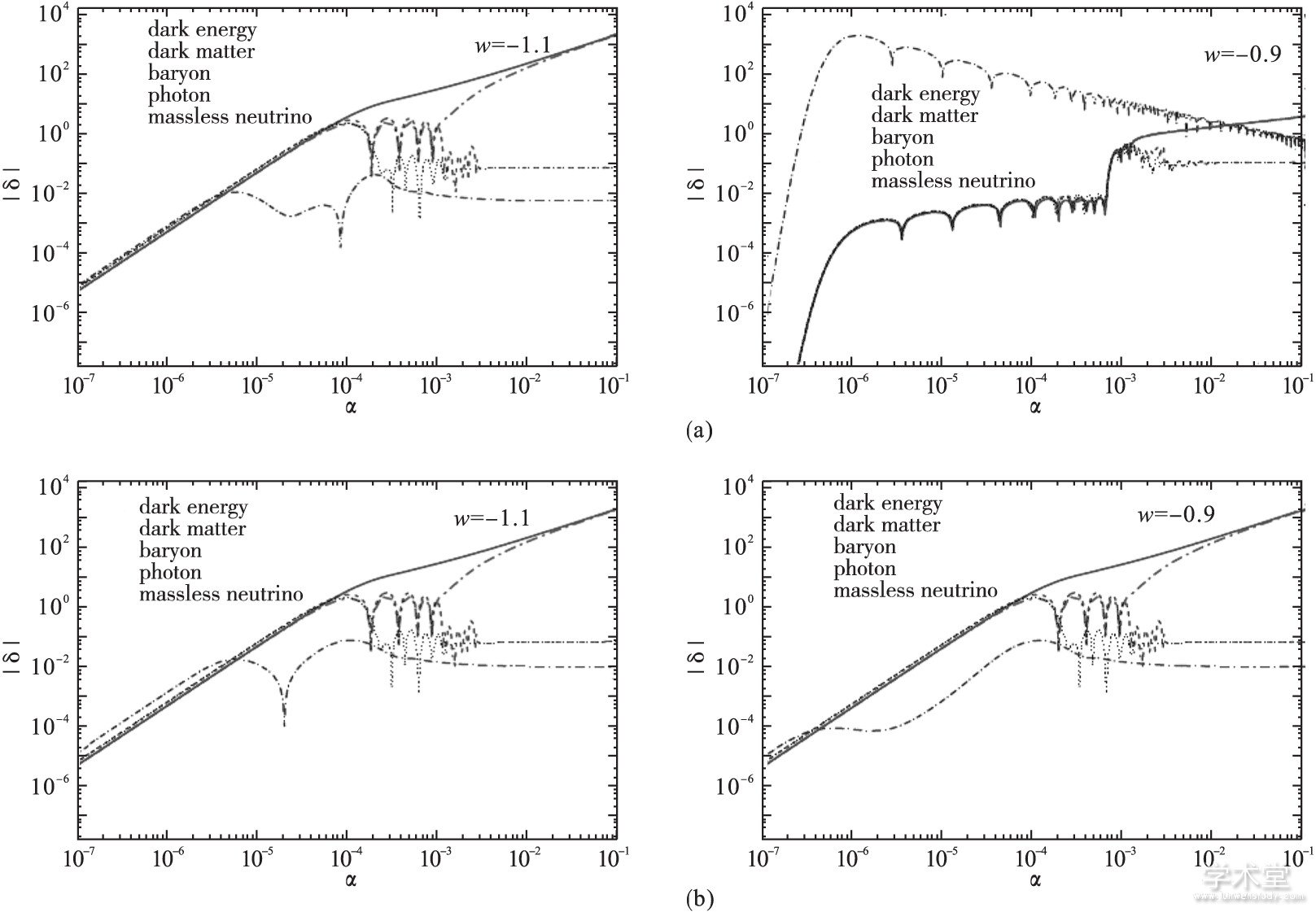
(a) 由传统方法计算获得; (b) 在扩展的PPF框架下计算获得。可见, w> -1情况的扰动发散问题被PPF方法成功解决。因此, 可利用观测数据对相互作用暗能量模型的完整参数空间进行探测。取自Y. H. Li, J. F. Zhang & X. Zhang, Phys. Rev. D 90 (2014) 063005。
我们已建立了一个完善的计算相互作用暗能量的宇宙膨胀历史和结构增长历史的理论框架, 使之适用于任意暗能量理论模型和任意相互作用模型, 并编写出可以向国际同行公开的计算程序.我们把该程序包命名为IDECAMB, 该程序包具有如下特点:1) 利用统一的参数化方法把所有的暗能量模型 (包括暗能量流体、标量场暗能量、全息暗能量等) 和相互作用项 (任意相互作用假设的相对论四维协变形式) 都包括进来;2) 向下兼容非耦合暗能量的PPF框架, 既可消除由相互作用项引起的扰动不稳定性, 也可消除由w越过-1所引起的不稳定性;3) 可计算任意宇宙学观测量;4) 只需要设定好参数化中的参数选取 (将不需要的参数设为零, 需要的保留) , 即可实现任意具体的相互作用暗能量模型, 选取好观测数据后, 即可直接进行计算, 对宇宙学参数进行观测限制;5) 可利用观测数据 (包括宇宙膨胀历史和结构增长的数据) 对相互作用暗能量模型的完整参数空间进行探测.
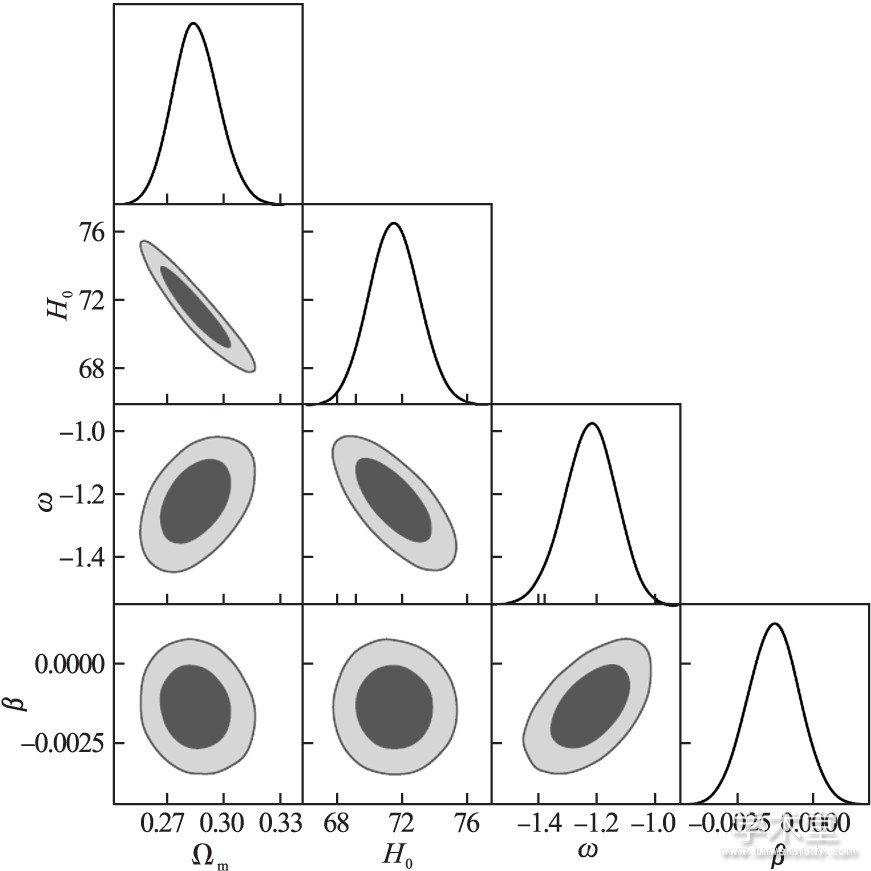
图3 利用当前观测数据对相互作用暗能量模型 (Q正比于暗物质密度的模型) 的限制。可见, 利用相互作用暗能量的PPF方案可对模型完整的参数空间进行探索。取自Y. H. Li, J. F. Zhang & X. Zhang, Phys. Rev. D 90 (2014) 063005。
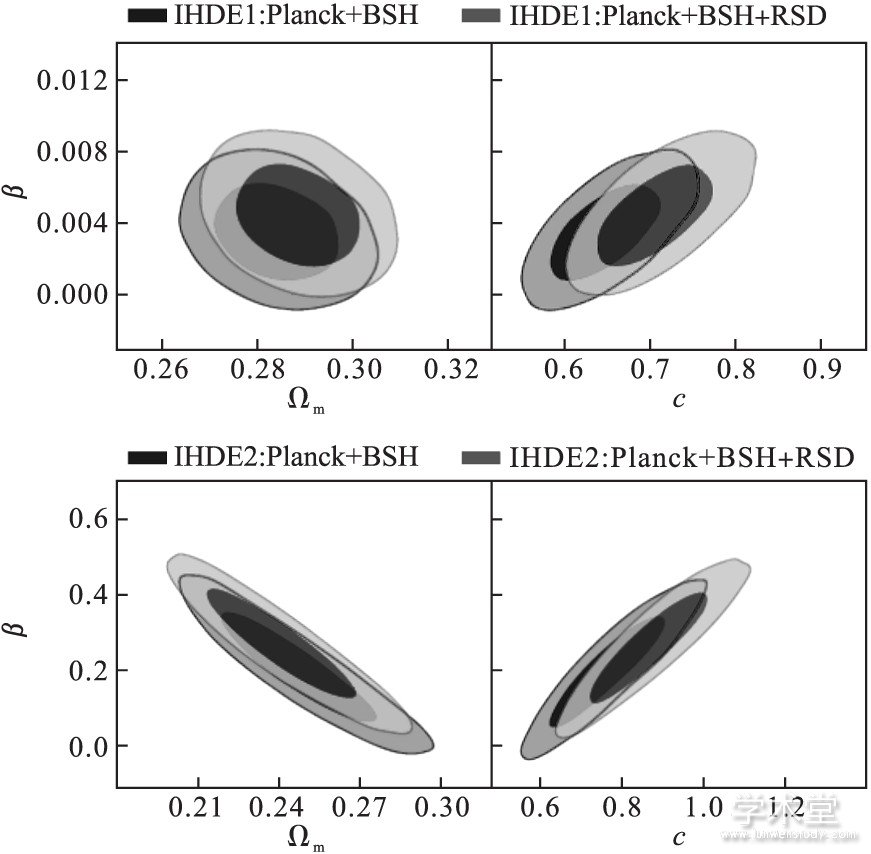
我们将模型比较应用到相互作用全息暗能量的研究中[19,20].考虑了五种典型的相互作用形式并进行比较, 发现在全息暗能量框架下, 非线性相互作用形式是最被当前观测数据所支持的, 与冷暗物质密度成正比的相互作用形式相对来说是最不被当前观测所支持的模型.对于正比于暗能量密度的形式和非线性相互作用形式, 观测数据可以以2σ统计显着性探测到一个正的耦合常数, 意味着支持暗能量衰变为暗物质的模型.进一步, 我们还首次在相互作用全息暗能量模型中考虑了宇宙学扰动, 利用扩展的PPF方法计算了宇宙学扰动的演化, 在此基础上利用包括红移空间畸变测量在内的宇宙学观测数据对相互作用全息暗能量模型进行了限制 (图4) [16].该工作的意义在于, 首次在相互作用全息暗能量模型中计算宇宙学扰动, 并利用大尺度结构的数据 (结构的增长) 来限制该模型.得到的结果显示, 在红移空间畸变测量的帮助下可以在2.95σ统计显着性水平上支持一类全息暗能量框架下的耦合形式.
图4 利用包括红移空间畸变测量在内的观测数据对相互作用全息暗能量模型的限制。取自L. Feng, Y.-H. Li, F. Yu, J.-F. Zhang & X. Zhang, Eur. Phys. J. C 78 (2018) 865。
3 、在宇宙学中称重中微子与搜寻惰性中微子的研究
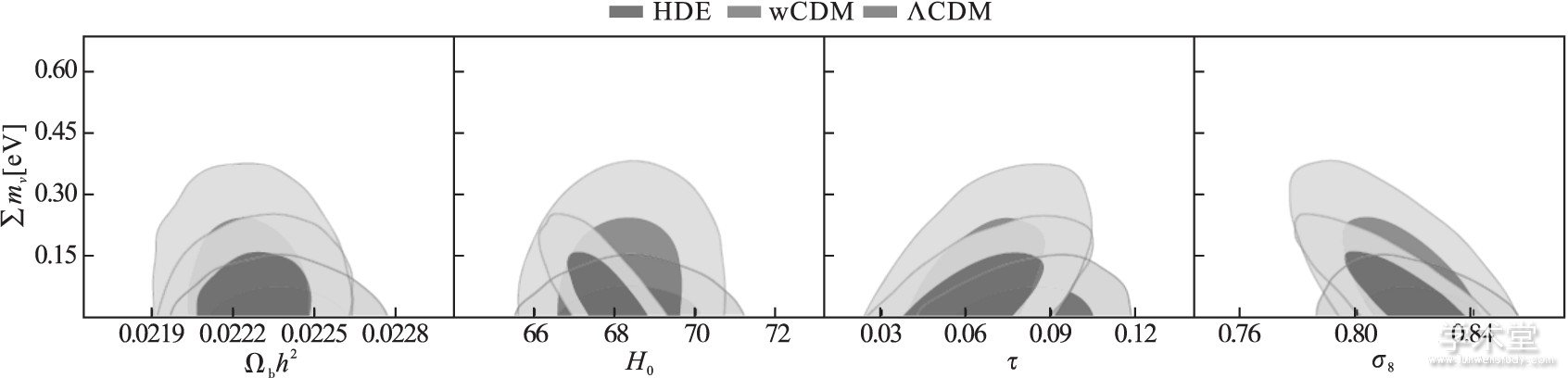
暗能量性质对于宇宙学称重中微子的影响.太阳与大气中微子振荡实验已显示中微子有质量, 而且不同中微子味道之间有混合.然而, 测量中微子的绝对质量对于粒子物理实验来说是一项重要挑战, 因为中微子振荡实验仅能测量不同中微子质量本征态之间的质量平方差, 而不能测量中微子的绝对质量.而且, 目前的中微子振荡实验还无法确定中微子的质量排序 (质量等级) .然而宇宙学观测却可以探测中微子绝对质量的效应, 因此利用宇宙学观测数据来限制中微子质量对于中微子研究有重要的意义.普朗克卫星任务所获取的宇宙微波背景温度和极化数据已经对中微子质量提供了严格的限制.对于ΛCDM模型, 利用普朗克温度谱数据结合重子声学振荡测量, 可得中微子质量上限 (95%置信度) 为0.21 eV;若将普朗克极化数据也加进来, 可得中微子质量上限为0.17 eV[1].但是我们应该注意到, 宇宙学称重中微子并不是直接测量中微子质量, 而是利用各种宇宙学观测数据来对包括中微子质量在内的各种宇宙学参数进行整体拟合, 因此暗能量的性质很可能对中微子质量拟合有重要的影响.因此, 定量研究暗能量性质如何影响宇宙学称重中微子是非常重要的课题.我们的工作[21]对此进行了深入研究, 考虑了两种重要的暗能量模型, 它们都是对ΛCDM模型的单参数扩展, 分别为wCDM模型和全息暗能量模型.我们利用普朗克最新的温度和极化数据, 结合其他的低红移观测, 包括重子声学振荡、Ia型超新星、哈勃常数测量、普朗克引力透镜测量, 对这些宇宙学模型进行拟合.我们发现, 一旦考虑了动力学暗能量, 中微子质量与哈勃常数之间的简并关系就会发生改变:在ΛCDM模型中, 中微子质量与哈勃常数之间是反相关的关系, 但是在wCDM模型和全息暗能量模型中, 中微子质量与哈勃常数之间的相关性变成了正相关 (图5) .相较于ΛCDM模型, 我们发现在wCDM模型中中微子质量限制变得松得多, 但是在全息暗能量模型中, 中微子质量却被限制得紧得多 (图5) .在全息暗能量模型中中微子质量上限变小是一个重要的发现.我们得到全息暗能量模型中中微子的质量上限 (95%置信度) 为0.105 eV, 这可能是迄今为止利用宇宙学观测数据称重中微子所得到的最严格的中微子质量上限.我们知道, 对于反质量等级, 中微子的质量下限大约为0.1 eV, 我们所得到的结果已经快要接近反质量等级的下限, 因此这个结果已经接近可以对中微子质量排序进行诊断.如果未来的中微子振荡实验 (比如江门中微子实验) 可以确定中微子质量等级, 若结果为反质量等级, 那么与我们的结果相结合就可以证伪全息暗能量模型.在这个研究中, 我们考虑的是简并中微子模型.但目前宇宙学观测已经能够将中微子总质量限制到了约0.2 eV的程度, 简并中微子模型已经开始变得不合适了, 因此我们接下来考虑了中微子质量劈裂的效应, 即考虑了不同的质量等级在宇宙演化中产生的效应 (图6) [22].我们的结果显示, 尽管正质量等级倾向于更被观测数据支持, 但是当前的宇宙学观测数据仍然不足以对质量等级的最终确定提供充分的证据.这方面的研究有重要的意义, 因此相关的工作仍在推进之中.
图5 利用当前观测数据对中微子总质量的限制。考虑了三种不同的暗能量模型, 包括标准模型、w为常数的模型和全息暗能量模型。图中显示了中微子质量与其他参数的相关性, 发现中微子质量与哈勃常数的相关性在标准模型中是反相关, 但在动力学暗能量模型中是正相关。不同的动力学暗能量可导致中微子质量上限变大或者变小。取自X. Zhang, Phys. Rev. D 93 (2016) 083011。
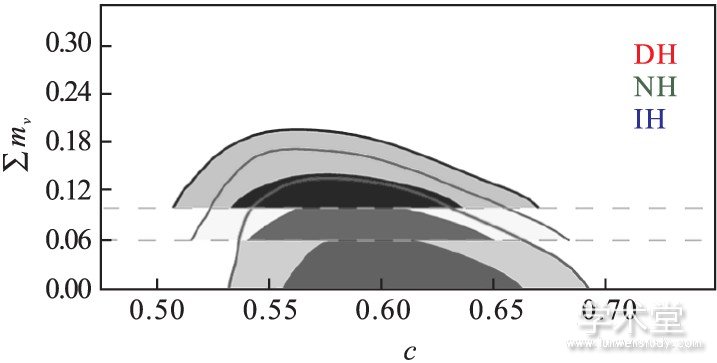
我们在论文[23]中总结了在这一研究方向获得的一些发现.利用宇宙学数据对中微子进行称重并不是对中微子质量的直接测量, 而是利用各种观测数据对包含中微子质量在内的各种宇宙学参数进行整体拟合, 因此暗能量的性质就有可能对中微子质量拟合产生重要影响.具体影响可以总结为: (a) 在动力学暗能量模型中, 中微子质量与哈勃常数之间的相关性由标准模型 (宇宙学常数冷暗物质模型) 中的反相关变为正相关[21]. (b) 在动力学暗能量宇宙中, 中微子质量上限既可以变大, 也可以变小;在幽灵和早期幽灵模型中, 中微子质量限制变得更宽松, 而在精质和早期精质模型中, 中微子质量限制变得更紧[21,22,24]. (c) 在全息暗能量模型中可以得到迄今为止最紧的中微子质量上限 (1.05 eV) , 已经几乎等于反等级情况的中微子质量下限, 因此该项研究与未来江门中微子实验的质量排序测量结果相结合有可能提供一种可证伪全息暗能量模型的方案[21,22]. (d) 中微子质量排序可以影响宇宙学拟合, 正等级情况要比反等级情况拟合得更好 (相同情况下卡方减少2-4) [22].此外, 暗能量与暗物质的耦合也会对中微子的宇宙学称重产生影响[14,17].
图6 利用当前观测数据对全息暗能量模型中微子质量的限制。考虑了不同的中微子质量等级。发现当前的宇宙学观测已开始变得对中微子质量排序有一定的敏感性。取自S. Wang, Y. F. Wang, D. M. Xia & X. Zhang, Phys. Rev. D 94 (2016) 083519。
惰性中微子的宇宙学搜寻.关于Z粒子宽度测量的实验结果已表明只有三代参与弱相互作用的中微子.但是在20世纪90年代, 美国洛斯阿拉莫斯实验室液体闪烁体中微子探测器 (LSND) 实验的数据显示, 似乎中微子具有4种味道, 而不是标准的3种味道.美国费米实验室的微型增强器中微子实验 (MiniBooNE) 也报告说, 发现了第四种中微子的迹象.第四种中微子并不直接参与弱相互作用, 因此被称为惰性中微子.中微子振荡实验显示, 惰性中微子的质量约为1 eV, 它们虽然不直接参与弱相互作用, 但是与其他中微子味道之间存在混合, 根据混合角推断它们在宇宙早期被完全热化.寻找惰性中微子存在的进一步充分证据是中微子研究中的重要课题.除了通过中微子振荡实验 (短基线或反应堆实验) 来寻找惰性中微子之外, 根据它们有质量的性质, 还可以在宇宙学数据中搜寻惰性中微子存在的证据.我们的工作[25]利用最新的宇宙学观测数据对惰性中微子进行了搜寻.我们的结果表明, 当前的宇宙学观测数据可在1.44个标准偏差置信水平上给出无质量惰性中微子存在的迹象, 而且考虑额外的无质量惰性中微子确实可以在一定程度上缓解宇宙学数据之间的不一致, 并可以改进宇宙学拟合.对于有质量惰性中微子, 当前的观测数据只能给出其有效质量的一个相当紧的上限.进一步的分析表明, 相较于无质量情况, 有质量惰性中微子并不被当前观测数据所支持.我们的结果与最近大亚湾与MINOS合作组所做的中微子振荡实验的结果以及IceCube合作组所做的宇宙线实验的结果是相一致的.我们在论文[26]中进一步分析了在全息暗能量宇宙学中搜寻惰性中微子的情况, 我们发现在全息暗能量模型中, 惰性中微子的存在确实可以很好地解释观测数据的不一致性, 但是这样的模型的数据拟合表现得并不好, 因此利用惰性中微子来解释数据矛盾的做法似乎正在失去吸引力.在论文[27]中, 我们进一步分析了利用惰性中微子是否可以解释增长指数测量的不一致性.在广义相对论中, 增长指数的理论预期值约为0.55, 修改引力理论可以得到比该值大的增长指数值, 比如DGP理论预言该值为0.68.利用红移空间畸变测量可以限制增长指数, 得到的结果确实比0.55大了约2σ.以前的研究表明, 考虑惰性中微子之后可以有效降低增长指数的限制值, 但是我们最近的工作显示, 在观测数据变得更精确之后, 惰性中微子已经不能在该问题上有效地发挥作用了.在论文[18,28]中, 我们还研究了在动力学暗能量和相互作用暗能量的宇宙中搜寻惰性中微子的情况.
4、 遗迹中微子在银河系中的引力结团研究
标准宇宙学模型预言, 在宇宙大爆炸后1 s左右, 中微子从热浴中退耦, 形成宇宙中微子背景.这些最古老的中微子是宇宙大爆炸的遗迹之一, 也被称为宇宙的遗迹中微子.宇宙演化至今, 这些宇宙遗迹中微子的平均数密度约为每立方厘米336个 (包含各种味道的中微子和反中微子;对于每种味道态的中微子, 其平均数密度约为每立方厘米56个) .宇宙遗迹中微子的实验探测是基础物理中的重要课题, 其意义十分重大, 既是对标准宇宙学模型的直接检验, 也可通过对这些古老中微子的探测将我们对宇宙的理解推至宇宙年龄仅为1 s的时期.尽管标准宇宙学模型对遗迹中微子的平均数密度做出了精确的预言, 但是在实际的探测计划中还需考虑引力的因素.中微子的非零质量导致它们会感受到银河系中暗物质和重子物质的引力, 因此在地球附近遗迹中微子的实际数密度会高于其平均值.正因如此, 对遗迹中微子在银河系中引力结团的研究已成为未来宇宙中微子背景实验探测研究中的必要环节.
我们在宇宙遗迹中微子的引力结团效应研究中取得重要进展:在N单体模拟中发展了一种重要的计算方法 (重加权方法) , 使得只利用一次模拟即可得到不同中微子质量和相空间分布下的中微子密度轮廓.该计算方法将在未来的宇宙中微子背景探测实验及其相关的唯象研究中发挥重要作用.该项研究成果已于2018年5月9日在《自然·通讯》上发表[29].
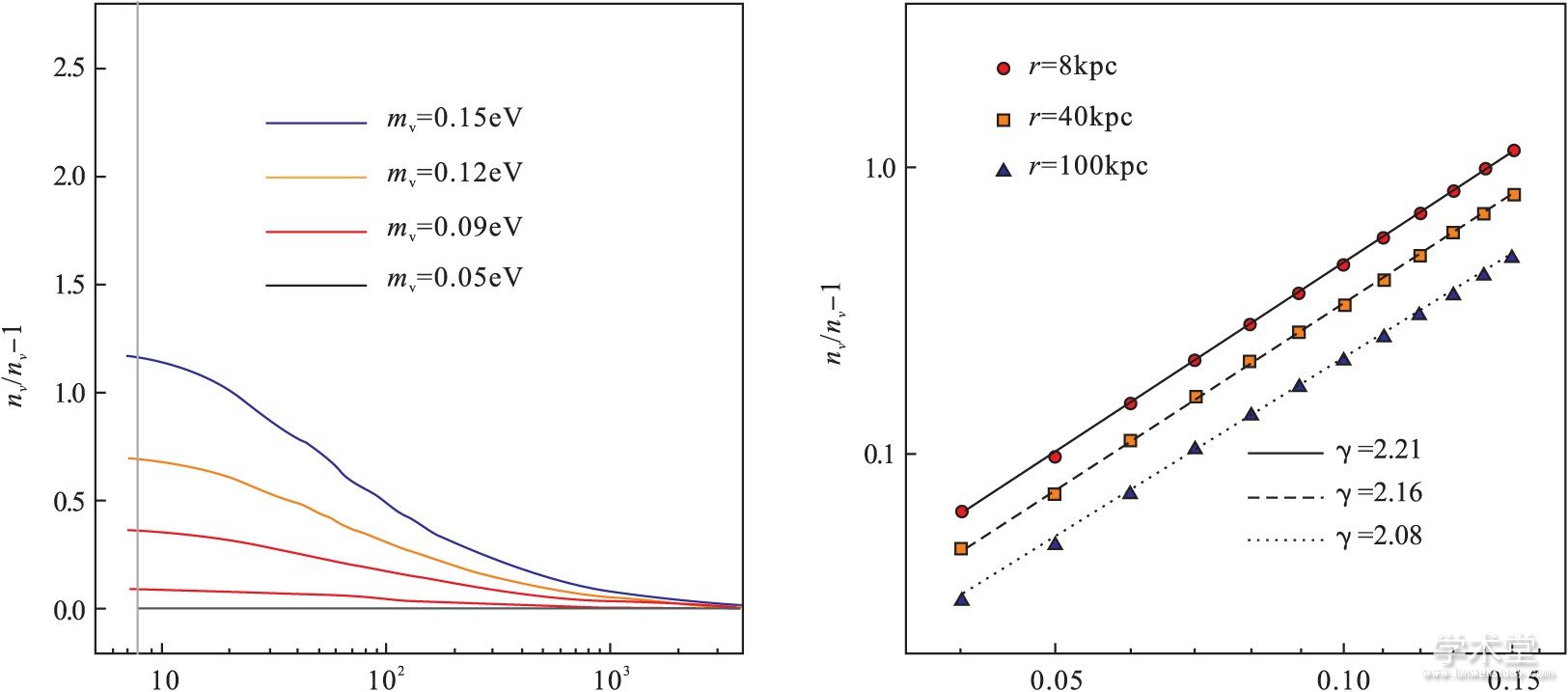
我们在研究中注意到, 中微子运动所遵循的哈密顿方程可以被改写成不依赖于质量的形式, 因此在N单体模拟中最终重构出的中微子密度轮廓只取决于每个测试粒子在相空间中所携带的权重.只需运行一次基准模拟计算 (在计算中设定确定的中微子质量和相空间初始分布) 并利用所得到的各个中微子测试粒子演化轨迹和相空间切分, 即可通过“重加权”技术进一步得到其他中微子质量和相空间分布下的中微子密度轮廓结果.这种方法极大地节省了计算资源, 在几分钟之内即可获得原本需要数周时间计算所得到的结果.利用该方法, 我们发现在宇宙学观测所支持的小中微子质量区域地球附近中微子密度涨落几乎正比于中微子质量的平方 (图7) .对于即将开展的旨在探测宇宙中微子背景的“托勒密” (PTOLEMY) 实验计划, 我们利用该方法计算了引力结团效应对于遗迹中微子俘获率的影响, 并对相关的中微子质量等级和新物理效应等问题进行了深入探讨.我们提出的“重加权”计算方案极大地促进了宇宙遗迹中微子引力结团的研究, 该方法也确信将在未来的宇宙中微子背景探测实验以及相关的唯象研究中发挥重要作用.
图7 热遗迹中微子在银河系中的引力结团效应。取自J. Zhang & X. Zhang, Nature Communications 9 (2018) 1833.
5、 利用引力波观测开展宇宙学参数估计的研究
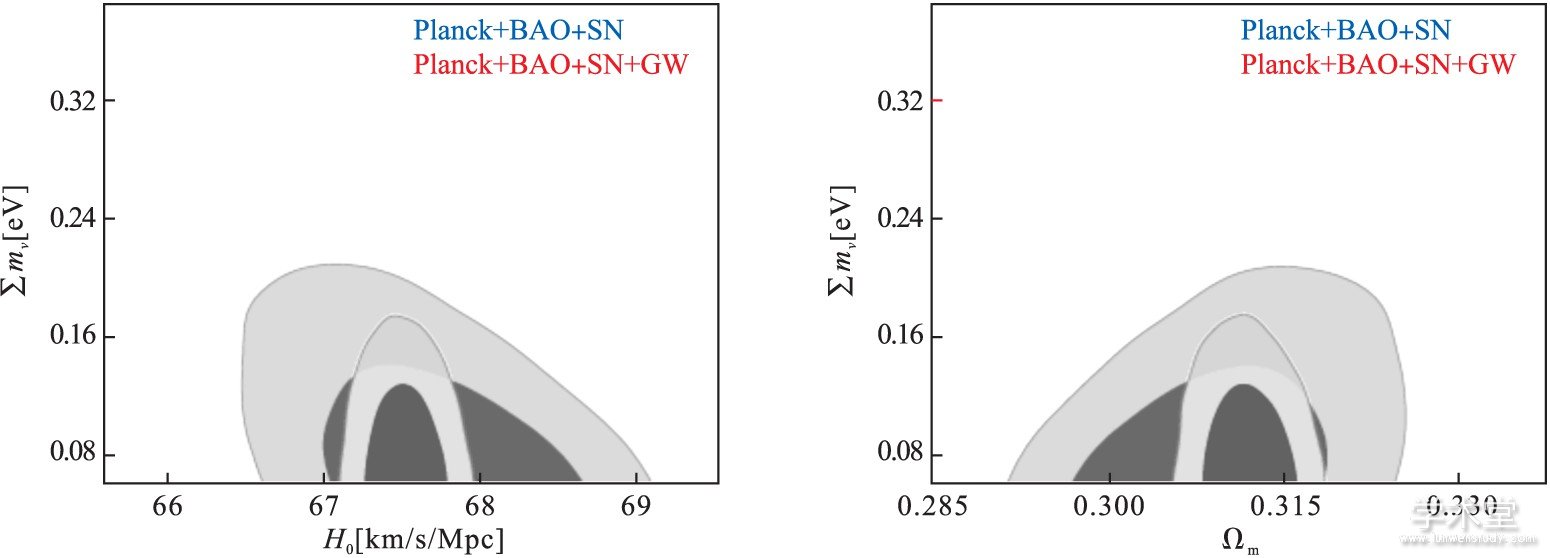
利用爱因斯坦望远镜的引力波观测改进宇宙学参数估计.对致密双星并合所产生的引力波的测量中包含了光度距离的信息, 因此如果能够同时对并合事件所产生的引力波信号和电磁信号 (双中子星系统或者中子星-黑洞系统) 进行精确测量, 就可以建立起一个真正的光度距离-红移关系.因此, 引力波观测可以作为宇宙的“标准汽笛”, 如果可以大量观测到此类引力波事件, 即可把引力波观测发展为一个宇宙学的新探针.当前, 宇宙学的主流探针主要包括宇宙微波背景各向异性测量 (温度和极化谱) 、重子声波振荡、Ia型超新星观测、哈勃常数直接测量等.此外, 还有对于宇宙大尺度结构增长历史的一些观测, 包括弱引力透镜星系剪切测量、星系团计数 (SZ效应) 、宇宙微波背景的透镜测量等.利用当前这些观测数据进行宇宙学参数估计时出现一些问题, 主要包括: (1) 参数之间存在简并, 一些参数之间的相关性较强; (2) 某些观测之间存在较显着的不一致性.引力波“标准汽笛”观测在打破参数简并方面具有独特的优势, 其原因在于此类观测可以测量真正的光度距离, 而超新星观测实际上只能测量不同红移处的光度距离的比值而不是真正的光度距离.我们的研究目标是, 定量化研究未来的引力波观测数据如何打破宇宙学参数之间的简并, 在宇宙学参数估计中发挥何种作用.为达到此目标可采取如下三个步骤: (1) 利用当前的各种宇宙学探针进行参数估计, 研究参数之间的简并以及如何消除不同探针之间的不一致性. (2) 研究未来的引力波观测数据 (爱因斯坦望远镜项目、LISA项目、太极计划项目等的模拟数据) 如何改进当前宇宙学观测的参数估计. (3) 研究未来的引力波观测如何与未来的其他观测 (WFIRST项目、Euclid项目、LSST项目、SKA项目等) 相结合来进行宇宙学参数估计.我们对爱因斯坦望远镜的引力波观测数据 (双中子星系统和中子星-黑洞系统) 进行了模拟, 研究其十年观测 (假设观测到1000个可用的引力波多信使事件) 对宇宙学参数估计所产生的影响[30,31].基于第一步的研究, 我们已对当前宇宙学探针所导致的参数简并情况有所了解, 如物质密度参数、哈勃常数、暗能量状态方程参数以及中微子质量等参数之间的简并情况和相关性关系.在此基础上, 我们研究爱因斯坦望远镜的引力波数据如何打破参数简并以及对宇宙学参数估计的精度提高至何种程度.我们发现, 相较于当前的宇宙学探针 (普朗克观测、重子声波振荡观测和超新星观测) , 引力波观测可以极大地提高物质密度和哈勃常数的限制精度, 对于暗能量状态方程参数的限制也有非常大的改善 (图8) .具体地, 对于标准的宇宙学常数冷暗物质模型, 哈勃常数的限制精度从0.68%提升至0.24%, 物质密度的精度从1.97% 提升至0.77%;对于状态方程参数为常数的暗能量模型, 哈勃常数的精度从1.53%提升至0.35%, 物质密度的精度从3.08%提升至0.75%, 暗能量状态方程参数的精度从4.1%提升至2.0%[30].进一步, 我们发现, 引力波观测数据还可以改善中微子质量的限制 (图9) .当不考虑引力波数据时, 对于正等级、倒等级和简并质量的情况, 得到的中微子质量上限分别为:0.175 eV, 0.200 eV和0.136 eV.当结合了引力波数据, 我们得到各情况的上限值为:0.151 eV, 0.185 eV和0.122 eV.可见, 在考虑引力波数据之后, 对应于三种情况 (正等级、倒等级和简并质量) , 中微子质量上限分别减小13.7%, 7.5%和10.3%[31].
图8 爱因斯坦望远镜的引力波标准汽笛观测模拟数据和当前观测数据对暗能量模型的限制。尽管引力波数据单独对暗能量状态方程参数的限制并不理想, 但是由于引力波数据可以有效打破其他观测导致的参数简并, 当跟其他观测联合时即可大幅度提高对状态方程参数的限制精度。取自X. N. Zhang, L. F. Wang, J. F. Zhang & X. Zhang, Phys. Rev. D (2019) , in press。
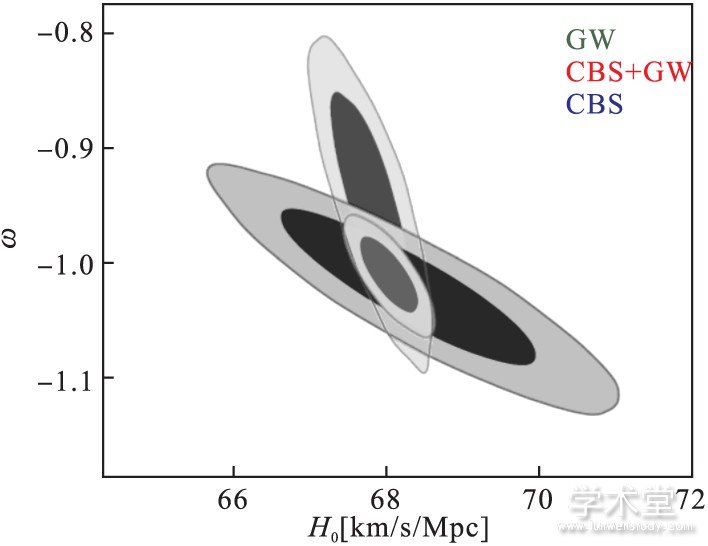
图9 利用爱因斯坦望远镜的引力波标准汽笛观测模拟数据和当前观测数据对中微子质量等参数的限制。考虑了中微子质量的正等级情况。取自L.F. Wang, X. N. Zhang, J. F. Zhang & X. Zhang, Phys. Lett. B 782 (2018) 87。
6、 暴胀宇宙学模型的观测限制研究
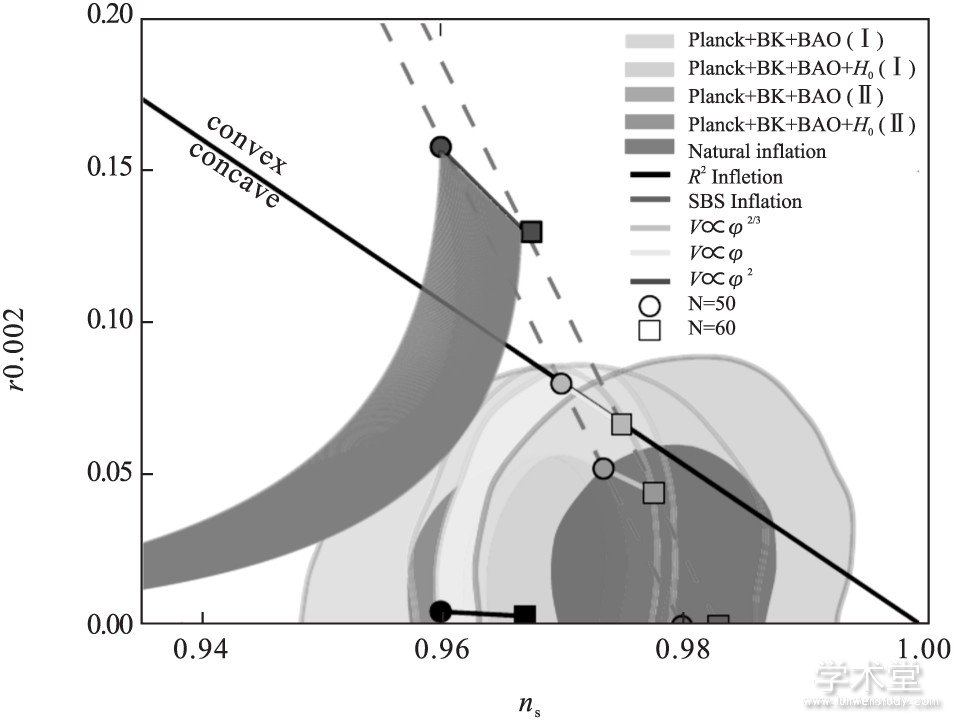
暴胀宇宙学模型的观测限制与筛选.我们在论文[32]中讨论了最新的哈勃常数测量结果对于暴胀宇宙学模型筛选的影响.利用观测数据对原初标量扰动谱指数和原初引力波幅度的限制结果, 可以有效地对暴胀宇宙学模型进行筛选.最新的哈勃常数直接测量结果与普朗克观测基于标准宇宙学模型所得到的限制结果有更大的不一致性, 为了解释这个矛盾, 在宇宙学模型中考虑某种暗辐射 (即额外的中微子有效代数参数) 是一个较为有效的方案, 这是因为有效代数参数与哈勃常数之间存在正相关.在观测数据中考虑哈勃常数测量并在模型中考虑有效代数参数可以显着地改变对原初标量扰动谱指数和原初引力波幅度的限制结果 (可以使标量谱指数变大, 因为它与有效代数和哈勃常数呈正相关) , 因此可以对暴胀宇宙学模型的筛选产生重要的影响.结果表明 (图10) , 在新的限制下, 最受支持的模型是自发破缺超对称暴胀模型, 而不是斯塔罗宾斯基模型 (它已处于2倍标准偏差置信区间的边缘) .对膜暴胀模型的讨论, 见论文[33].
图10 最新的哈勃常数测量结果对于暴胀宇宙学模型筛选的影响。利用观测数据对原初标量扰动谱指数和原初引力波幅度的限制。取自R. Y. Guo& X. Zhang, Eur. Phys. J. C 77 (2017) 882。
反弹暴胀宇宙学模型的观测限制研究.反弹宇宙学模型可以避免宇宙的大爆炸奇点, 在反弹点之后接上一段暴胀阶段的模型就是反弹暴胀宇宙学模型, 该模型可用于解释宇宙微波背景辐射各向异性角功率谱在大尺度上的一些特征.我们在论文[34]中利用高阶导数项提出了一个一般的原初功率谱的参数化形式, 其中包括了典型的反弹参数, 比如反弹时间尺度、能标等, 进而我们利用当前的观测数据对反弹暴胀模型进行了限制, 我们发现反弹模型可以很好地解释宇宙微波背景的观测, 特别是在温度功率谱大尺度上的功率压低和振荡现象.
7、 结论
根据当前的观测数据, 宇宙学常数模型仍是所有暗能量模型中最好的模型, 而且一些动力学暗能量模型已经被当前的观测数据排除了.利用红移漂移的10年观测数据即可在很大程度上改进利用哈勃参数测量对暗能量的限制.利用我们发展的扩展的PPF方法和我们编写的IDECAMB程序包可以有效计算相互作用暗能量的宇宙学扰动, 避免发散问题, 并可利用观测数据对任意相互作用暗能量模型的参数空间进行完整的探索.暗能量的性质可以对中微子质量的宇宙学测量产生重要的影响, 相比于宇宙学常数模型, 在动力学暗能量模型中中微子质量的上限值既可能变大也可能变小.当前的观测数据已经开始对中微子质量的排序情况作出可能的诊断, 即中微子质量排序已经可以影响当前的宇宙学拟合, 结果显示正等级情况比倒等级情况拟合得更好.在当前的宇宙学观测数据中并未找到轻质量惰性中微子存在的确切证据.在遗迹中微子的银河系结团效应的研究中, 在N单体模拟中可以发展出一种重加权方法, 只需一次基准计算即可得到任意中微子质量和相空间分布下的中微子密度轮廓结果, 极大地提升了计算效率, 该计算方案极大地促进了宇宙遗迹中微子引力结团的研究, 将在未来中微子背景探测实验中发挥重要作用.引力波标准汽笛观测将在宇宙学参数估计中发挥重要作用, 爱因斯坦望远镜的模拟数据显示, 引力波数据将有效打破当前宇宙学探针所形成的参数简并, 极大地提高参数估计的精度.
参考文献
[1] Planck Collaboration.Planck 2015 results[J].XIII.Cosmological parameters, Astronomy and Astrophysics, 2016, 13:594.
[2] Planck Collaboration.Planck 2013 results[J].XVI.Cosmological parameters, Astronomy and Astrophysics, 2014, 16:571.
[3] Yue-Yao Xu, Xin Zhang.Comparison of dark energy models after Planck 2015[J].European Physical Journal, 2016, 76:588.
[4] Jia-Jia Geng, Jing-Fei Zhang, Xin Zhang.Quantifying the impact of future Sandage-Loeb test data on dark energy constraints[J].Journal of Cosmology and Astroparticle Physics, 2014, 1407:6.
[5] Jia-Jia Geng, Jing-Fei Zhang, Xin Zhang.Parameter estimation with Sandage-Loeb test[J].Journal of Cosmology and Astroparticle Physics, 2014, 12:18.
[6] Jia-Jia Geng, Yun-He Li, Jing-Fei Zhang, et al.Redshift drift exploration for interacting dark energy[J].European Physical Journal , 2015, 75:356.
[7] Dong-Ze He, Jing-Fei Zhang, Xin Zhang.Redshift drift constraints on holographic dark energy[J].Science China Physics, Mechanics & Astronomy, 2017, 60, 039511.
[8] Rui-Yun Guo, Xin Zhang.Constraining dark energy with Hubble parameter measurements:an analysis including future redshift-drift observations[J].European Physical Journal , 2016, 76:163.
[9] Jia-Jia Geng, Rui-Yun Guo, Anzhong Wang, et al.Prospect for cosmological parameter estimation using future Hubble parameter measurements[J].Communications in Theoretical Physics, 2018, 70:445.
[10] J Valiviita, E Majerotto, R Maartens.Instability in interacting dark energy and darkmatter fluids[J].JCAP, 2008, 7:20.
[11] Yun-He Li, Jing-Fei Zhang, Xin Zhang.Parametrized post-Friedmann framework for interacting dark energy[J].Physical Review , 2014, 90:063005.
[12] Yun-He Li, Jing-Fei Zhang, Xin Zhang.Exploring the full parameter space for an interacting dark energy model with recent observations including redshift-space distortions:Application of the parametrized post-Friedmann approach[J].Physical Review , 2014, 90:123007.
[13] Yun-He Li, Jing-Fei Zhang, Xin Zhang.Testing models of vacuum energy interacting with cold dark matter[J].Physical Review , 2016, 93:023002.
[14] Rui-Yun Guo, Yun-He Li, Jing-Fei Zhang, et al.Weighing neutrinos in the scenario of vacuum energy interacting with cold dark matter:application of the parameterized post-Friedmann approach[J].Journal of Cosmology and Astroparticle Physics, 2017, 1705:40.
[15] Xin Zhang.Probing the interaction between dark energy and dark matter with the parametrized post-Friedmann approach[J].Science China Physics, Mechanics & Astronomy, 2017, 60:050431.
[16] Lu Feng, Yun-He Li, Fei Yu, et al.Exploring interacting holographic dark energy in a perturbed universe with parameterized post-Friedmann approach[J].European Physical Journal, 2018, 78:865.
[17] Rui-Yun Guo, Jing-Fei Zhang, Xin Zhang.Exploring neutrino mass and mass hierarchy in the scenario of vacuum energy interacting with cold dark matter[J].Chinese Physics, 2018, 42:095103.
[18] Lu Feng, Jing-Fei Zhang, Xin Zhang.Search for sterile neutrinos in a universe of vacuum energy interacting with cold dark matter[J].Physics of the Dark Universe, 2019, 23:100261.
[19] Lu Feng, Xin Zhang.Revisit of the interacting holographic dark energy model after Planck 2015[J].Journal of Cosmology and Astroparticle Physics, 2016, 1608:72.
[20] Hai-Li Li, Jing-Fei Zhang, Lu Feng, et al.Reexploration of interacting holographic dark energy model:cases of interaction term excluding the Hubble parameter[J].European Physical Journal, 2017, 77:907.
[21] Xin Zhang.Impacts of dark energy on weighing neutrinos after Planck 2015[J].Physical Review, 2016, 93:083011.
[22] Sai Wang, Yi-Fan Wang, Dong-Mei Xia, et al.Impacts of dark energy on weighing neutrinos:Mass hierarchies considered[J].Physical Review, 2016, 94:083519.
[23] Xin Zhang.Weighing neutrinos in dynamical dark energy models[J].Science China Physics, Mechanics & Astronomy, 2017, 60:060431.
[24] Ming-Ming Zhao, Yun-He Li, Jing-Fei Zhang, et al.Constraining neutrino mass and extra relativistic degrees of freedom in dynamical dark energy models using Planck 2015 data in combination with low-redshift cosmological probes:basic extensions to ΛCDM cosmology[J].Monthly Notices of the Royal Astronomical Society, 2017, 469:1713.
[25] Lu Feng, Jing-Fei Zhang, Xin Zhang.A search for sterile neutrinos with the latest cosmological observations[J].European Physical Journal, 2017, 77:418.
[26] Ming-Ming Zhao, Dong-Ze He, Jing-Fei Zhang, et al.Search for sterile neutrinos in holographic dark energy cosmology:Reconciling Planck observation with the local measurement of the Hubble constant[J].Physical Review, 2017, 96:043520.
[27] Ming-Ming Zhao, Jing-Fei Zhang, Xin Zhang.Measuring growth index in a universe with massive neutrinos:A revisit of the general relativity test with the latest observations[J].Physics Letters, 2018, 779:473-478.
[28] Lu Feng, Jing-Fei Zhang, Xin Zhang.Searching for sterile neutrinos in dynamical dark energy cosmologies[J].Science China-Physics, Mechanics & Astronomy, 2018, 61:050411.
[29] Jue Zhang, Xin Zhang.Gravitational clustering of cosmic relic neutrinos in the Milky Way[J].Nature Communications, 2018, 9:1833.
[30] Xuan-Neng Zhang, Ling-Feng Wang, Xin Zhang.Improving cosmological parameter estimation with gravitational wave observations from the Einstein Telescope[J].Physical Review, 2019, in press.
[31] Ling-Feng Wang, Xuan-Neng Zhang, Jing-Fei Zhang, et al.Impacts of gravitational-wave standard siren observation of the Einstein Telescope on weighing neutrinos in cosmology[J].Physics Letters, 2018, 782:87-93.
[32] Rui-Yun Guo, Xin Zhang.Constraints on inflation revisited:an analysis including the latest local measurement of the Hubble constant[J].European Physical Journal, 2017, 77:882.
[33] Rui-Yun Guo, Lei Zhang, Jing-Fei Zhang, et al.Constraints on brane inflation after Planck 2015:Impacts of the latest local measurement of the Hubble constant[J].Science China-Physics, Mechanics & Astronomy, 2019, 62:30411.
[34] Shu-Lei Ni, Hong Li, Tao-tao Qiu, et al.Probing signatures of bounce inflation with current observations[J].European Physical Journal, 2018, 78:608.





