
1 研究背景与问题提出
中学数学中有许多概念是不加定义的,比如“自然数”“集合”“点”“直线”“平面”等等,这些概念通常被称为“原始概念”.原始概念在数学上有着非常重要的意义,它们“不仅满足了人们在建立数学理论时必须有个出发点的需要,以此避免导致恶性循环或无穷倒退的窘境之中”,同时还“能使人们的思想从狭溢的概念内涵意义的束缚中解放出来,从而扩大了人们的视野和想象力,有可能发展出新的数学理论来”[1].在中学数学教材中,有些原始概念被直接回避,有些则采用描述性的方式去介绍。平面这一原始概念,教材一般是从客观存在的现实模型( 如平静的海面、桌面、地面等) 中引出,然后引导学生理解平面的无限延展性,同时还注重强调平面的表示方式。
对于平面这个原始概念,人们的理解情况如何呢? 数学教育工作者 Zormbala 和 Tzanakis 通过对51 位非数学专业毕业、从事各种职业的对象( 德文教师、心理学家、律师、医生等等) 的调查发现,他们的理解与历史上一些数学家的理解之间存在一定的相似性。[2]
历史相似性理论源于德国生物学家海克尔( E.Haeckel,1834 - 1919) ,他指出: 儿童的心理发展过程就是人类种族发展过程的重复。从 19 世纪末起,越来越多人支持“数学发展的历程与学生学习的过程存在相似性”的观点,其中包括法国数学家庞加莱( H. Poincaré,1854 - 1912) ,德国数学家克莱因( F. Klein,1849 -1925) ,匈牙利数学家拉卡托斯( I.Lakatos,1922 - 1974) 等。[3]
许多实证表明,学生对某些数学概念的认知与概念的历史发展之间具有相似性。
为研究我们的高中学生对平面概念的理解情况,确定如下两个研究问题: ( 1) 高中生是如何理解平面概念的? ( 2) 高中学生对平面概念的理解是否呈现出历史相似性?
2 平面概念的历史发展概述
追溯平面概念的历史发展,有利于我们更深刻地理解这一数学概念。
根据古希腊评注家普罗克拉斯( Proclus,公元 5世纪) 的记载,古希腊哲学家巴门尼德( Parmenides,公元前 5 世纪) 将几何对象分为三类: 平直的、弯曲的、平直与弯曲混合的。对于平面,巴门尼德的观点是: 平面是直线在其中可以以任意方向与其相合的表面。[4]
公元前 3 世纪,古希腊数学家欧几里得在《几何原本》中给出平面的定义如下[5]:“定义 I. 7 平面是它上面的线一样地平放着的面。”上述定义语义较为含糊,而且平面的存在性也有待通过构造的方式予以说明。面对欧几里得留下的问题,后世许多数学家做出了努力。[2]
古希腊数学家海伦( Heron,约公元 1 世纪) 给出了平面诸多具有相同特征---“平”的定义: 平面是直线与之完全相合的表面。如果一条直线经过表面上的两个点,那么这条直线的任意部位都和这个表面完全相合。
德国着名数学家莱布尼茨 ( G. W. Leibniz,1646 - 1710) 曾多次尝试消除欧几里得平面定义中的逻辑缺陷。在其着作 In Euclidis Prota( 大约 1696年) 和 Initia rerum mathematicarum metaphysica( 1714年至 1716 年) 中,莱布尼茨研究了一些基本的几何概念( 如直线、平面和圆) 的定义问题,并认为海伦对平面本质的描述是“重复语义的杂耍”.在给荷兰着名物理学家惠更斯( Christiaan Huygens,1629 -1695) 的信中,莱布尼茨以一种全新的方式定义了平面的概念: 平面是到两个已知点距离相等的点集。
在欧几里得之后,平面的构建问题一直困扰着数学家,莱布尼茨的这个定义则使之成为可能。
英国数学家辛松( R. Simpson,1687 - 1768) 认为,过表面上任意两点的直线与这个表面完全相合,这个表面就是平面。在 18 世纪至 19 世纪末期,大多数几何着作都认可这个定义。实际上,辛松的这个定义和海伦的定义是一致的。
19 世纪,许多着名数学家紧随莱布尼茨的步伐,其中包括德国数学家高斯( Carl Friedrich Gauss,1777 - 1855) 、匈牙利数学家 W. Bolyai 及其儿子 J.Bolyai.高斯将平面定义为: 过直线上一定点并与这条直线垂直的所有直线的表面; 而在对辛松的定义批判的同时,W. Bolyai 在空间中以运动的方式给平面下了定义: 在空间内,一条直线绕与其垂直的直线旋转所形成的图形; J. Bolyai 则继承了其父亲的思想,并创新性地把运动和对称同时引入平面的概念中。
19 世纪末,几何学有了飞跃性的发展,德国数学家希尔伯特( David Hilbert,1862 - 1943) 于 1899年发表了他的名着《几何基础》。在这本经典着作中,希尔伯特仍把“点”“直线”“平面”作为基本对象不加定义,并把“点在直线上”“点在平面上”“一点在另两点之间”“线段的合同( 相等) ”“角的合同( 相等) ”作为不加定义的基本对象之间的关系,称为基本关系,对它们也不加以说明或解释。三个基本对象和五个基本关系统称为基本概念,这些基本概念受五组、共 20 条公理的制约。除了这八个基本概念以外的任何几何对象、名词、术语、关系等等,都必须加以严格定义。[5]
综上所述,在希尔伯特之前,人们主要从直观经验( 先是局限于二维平面内而后是在三维空间中)来探究平面概念的本质,并试图在三维空间中构造出平面来; 希尔伯特之后,人们普遍接受了平面概念的逻辑本质,自此“平面”不再是需要定义的孤立的数学对象,它的全部意义存在于一组具有逻辑一致性的公理体系中。
3 研究方法
采用实证研究方法,通过问卷调查,对学生的解答进行定量与定性分析。
3. 1 样本
被试来自沪、滇两地三所中学,从高二年级随机选取六个班级,共278 人,其中男生153 名,女生125名,收回有效问卷共 270 份,其中上海 173 份,云南97 份。
3. 2 工具
测试卷由 Zormbala & Tzanakis 所用问题改编而成,共含 2 道题,分别为:
( 1) 你认为什么是平面?
( 2) 请你作出一个平面。测试时间为 15 分钟。
测试的主要目的是为了了解学生对平面概念的理解情况,并由此分析学生对平面概念的理解是否与概念的发展过程具有历史相似性。
4 结果与分析
从整体情况来看,测试结果反映了学生对平面概念的理解情况,以下是对测试结果的逐题分析。
4. 1 学生对测试题 1 的回答情况
测试结果: 回答分为 3 类,分别是第 1 类: 通过描述平面的与“水平”无关的性质; 第 2 类: 通过描述平面“水平”的性质或者通过举例描述的方式; 第3 类: 通过描述点、线与平面的位置关系。具体情况 如表 1 所示。【1】

对结果的分析: 可以看出所有学生对平面概念的理解都处于直观水平,没有学生认为“平面”是不需要定义的概念。大部分学生从实际生活中的例子或者从“平面”的字面涵义来说明什么是平面,尽管他们知道平面上的点、直线与平面之间的关系,但并未从这个角度来回答; 仅有不到四分之一的学生通过点、线与平面的位置关系来说明什么是平面( 其中的一种解答如图1) ,他们的理解与历史上数学家欧几里得、海伦以及辛松的理解类似,这其中还有 4 名学生动态地理解直线与平面的关系( 其中的一种解答如图 2) ,这与历史上数学家 W. Bolyai 的理解类似。
4. 2 学生对测试题 2 的回答情况
测试结果: 回答分为 4 类,分别是第 1 类: 作出一个平行四边形; 第 2 类: 作出其他图形; 第 3 类: 没有作出任何图形; 第 4 类: 指出平面无法做出。具体情况如表 2 所示。【2】
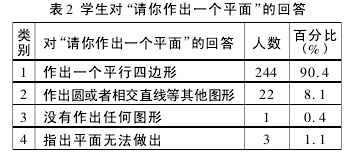
对结果的分析: 可以看出绝大部分学生受教材的影响,把“平面的表示”与“平面”本身相混淆,因而把平行四边形当作平面; 有 3 名学生表示平面是无法作出的( 其中的一种解答如图 3) ,体现了对平面概念理解的深刻性。
5 结论与建议
平面一直被广大的师生认为是一个极其基本和简单的几何概念,往往容易被忽视。通过以上的数据统计分析以及对学生具体答卷的分析,我们可以发现学生对这个基本几何概念的掌握不容乐观,并得出以下两个主要结论:
( 1) 绝大部分的高中生对平面概念的理解处于直观水平;( 2) 部分高中生对于平面概念的理解与历史上的数学家存在一定的相似性。
上述结论说明我们的现行教材和课堂教学还需要进一步完善。对此,给出具体建议如下:
( 1) 平面是立体几何的基本概念,在现阶段的高中教学中一般是从实物的形态抽象出平面的概念,在此过程中教师要尽量注意引导和带动学生发现几何中的平面与具体实物之间的区别,特别是平面的表示与平面本身之间的区别。这实际上就是要渗透数学的特点: 研究对象虽然是从现实世界抽象出来的,但抽象出来之后便存在人类的理想世界中。
( 2) 在平面概念的教学过程中,可以从点、线、面之间的位置关系,帮助学生从不同角度深入理解这个概念。
( 3) 由于部分高中生在平面的概念理解方面与历史上的数学家存在一定的相似性,因此,在教学过程中,教师可以通过学习一些数学的历史与文化,提前预期学生对于数学概念理解的困难,并针对这些困难相应得加强指导。
参考文献:
[1] 杜树芳。 谈数学原始概念的赋意性[J]. 大连教育学院学报。 1995,( 1 -2) :87 -89.
[2] Zormbala,K. ,Tzanakis,C. The concept of the plane ingeometry: elements of the historical evolution inherent inmodern views[J]. Mediterranean Journal for Research inMathematics Education,2004,3( 1 - 2) : 37 - 61.
[3] 赵瑶瑶,张小明。 关于历史相似性理论的讨论[J]. 数学教育学报。 2008,17( 4) :53.
[4] Proclus. A Commentary on the First Book of Euclid's Ele-ments ( 2nd Print edition) [M]. Glenn R. Morrow trans-late. Princeton: Princeton University Press. 1992.
[5] ( 古希腊) 欧几里得。 几何原本( 第 2 版) [M]. 兰纪正,朱恩宽,译。 西安: 陕西科学技术出版社。 2003.





