
数学是各个时代人类文明的标志之一,在河谷文明与早期数学至中世纪近代数学形成之前,经典代数学的核心内容就是方程理论. 其发展的轨迹主要经历了三个方面的演化,一是历经了从文字到符号化系统的抽象过程;二是历经了未知数的次数提高以及知数个数增多,即一元高次方程理论和方程组理论. 三是求解方程方法的演化与技巧研究. 这些问题都为古代数学到近代的发展起到了极重要的推进作用.中国数学从公元前后至公元 14 世纪,先后经历了两汉、魏晋南北朝、宋元时期三个发展高峰时期,其中宋元时期的成就,如珠算、天元术、四元术、大衍求一术、四元高次方程等,代表了中国古典数学的最高成就.
1 《九章算术》中的方程术
《九章算术》是算经十书中重要的一部数学专着. 据考证,大约成书于东汉初期.“方程”章还在世界数学史上首次阐述了负数及其加减运算法则;一次方程组问题,解线性方程组时使用的直除法,与矩阵的初等变换一致,这是世界上最早的完整的线性方程组的解法.如方程章第一题(见图 1):“今有上禾(指上等稻子)三秉(指捆),中禾二秉,下禾一秉,实(指谷子)三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗. 问上、中、下禾实一秉各几何?”【图1略】
这一题若按现代的记法,设 x、y、z 依次为上、中、下禾各一秉的谷子数,则上述问题是求解三元一次方程组:【1-3】

《九章算术》用算筹列式演算:“方程术曰,置上禾三秉,中禾二秉,下禾一秉,实三十九斗,于右方;中、左行列如右方;以右行上禾彳扁乘(即遍乘)中行而以直除(这里“除”是减,“直除”即连续相减. )……”. 将筹算数码转为阿拉伯数字,按意演算,则为:【公式】

“答曰:上禾一秉,九斗四分斗之一(914斗);中禾一秉,四斗四分斗之一(414斗);下禾一秉,二斗四分斗之三(234斗)”.
2 《孙子算经》《数书九章》与物不知数问题
《孙子算经》为算经十书之一,是公元四世纪左右的数学着作,作者不详. 现传本分上、中、下三卷. 上卷叙述度量衡制度、筹算记数和筹算乘除算法;中卷举例说明筹算分数算法、开平方和面积、体积计算;下卷是各种应用问题. 中、下两卷共有各类算题 64 道.《孙子算经》下卷“物不知数”题说:今有物,不知其数. 三三数之,剩二;五五数之,剩三;七七数之,剩二.问:物几何? 答曰:二十三.显然,这相当于求不定方程组 N =3x +2,N =5y +3,N =7z +2,的正整数解 N,或用现代数论符号表示,等价于解下列的一次同余组:N≡2(mod3)≡3(mod5)≡2(mod7).《孙子算经》题的术文指出解题的方法:三三数之,取数七十,与余数二相乘;五五数之,取数二十一,与余数三相乘;七七数之,取数十五,与余数二相乘. 将诸乘积相加,然后减去一百零五的倍数. 列成算式就是:N = 70 × 3 + 21 × 3 + 15 × 2 - 2 × 105.秦九韶 1247 年完成了数学名着《数书九章》,这部中世纪的数学杰作,在许多方面都有创造,其中求解一次同余组的“大衍求一术”,是在《孙子算经》中“物不知数”问题基础上,进一步研究,提出了“大衍求一术”,数论中称为“中国剩余定理”,也称“孙子定理”. 经我国历代数学家研究发展成完整严谨的理论与方法.比西方 1801 年着名数学家高斯(Gauss,1777-1855 年)建立的同余理论早 554 年. 秦九韶的任意次方程的数值解领先霍纳 572 年,秦九韶不仅为中国赢得巨大的荣誉,也为世界数学作出了杰出贡献.
3 《张丘建算经》的百钱百鸡
《张丘建算经》成书于公元 466-485 年间,张丘建属于北魏人. 该书共三卷 92 题,包括测量、纺织、交换、纳税、冶炼、土木工程、利息等各方面的计算问题.《张丘建算经》的最后一题是闻名于世的“百鸡问题”,即:“今有鸡翁一,直(值)钱五;鸡母一,直钱三;鸡雏三,直钱一. 凡百钱,买鸡百只,问鸡翁、母、雏各几何?”书中给出三组解:(1)鸡翁 4,鸡母 18,鸡雏 78;(2)鸡翁 8,鸡母 11,鸡雏 81;(3)鸡翁 12,鸡母 4,鸡雏 84.这是一个不定方程问题. 设鸡翁、鸡母、鸡雏的只数分别为 x,y,z,则可列出方程组:【公式2】
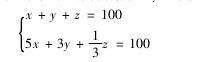
其解法则为:“鸡翁每增四,鸡母每减七,鸡雏每益(增加)三,即得. ”【公式3】

4 宋元时期的天元术与四元术
4. 1 天元术
宋代以前,数学家要列出一个方程,如唐代王孝通运用几何方法列三次方程,往往需要高超的数学技巧、复杂的推导和大量的文字说明,这是一件相当困难的工作. 随着宋代创立的增乘开方法的发展,解方程有了完善的方法,这就直接促进了对于列方程方法的研究,于是,出现了中国数学的又一项杰出创造———天元术.在李冶的《测圆海镜》(公元 1248 年)、《益古演段》(公元 1259 年)首先进行了系统阐述,是符号代数的尝试,在数学史上具有里程碑意义.用天元术列方程的方法是:首先“立天元一为某某”,就是现在的设未知数 x,一次幂系数的右旁记一“元”字,有时在常数右旁记一“太”字;其余各项按未知数的幂次相对于一次项上下递增或递减;系数是负数的,在系数的个位数码上加一斜划. 如图 2.表示方程:25x2+ 280x - 6905 = 0.【图.略】
4. 2 四元术
把天元术的原理应用于联立方程组,先后产生了二元术、三元术和四元术. 这是十三世纪中叶到十四世纪初我国宋元时期数学家又一辉煌成就. 现有传本的朱世杰(约1260-1320 年)的《四元玉鉴》就是一部杰出的四元术着作.所谓四元术,就是用天、地、人、物四元表示四元高次方程组. 列式的方法是:在常数右侧记一“太”字,天、地、人、物四元和它们的乘幂的系数分别列于“太”字的下、左、右、上,相邻两未知数和它们的乘幂的积的系数记入相应的两行相交的位置上,不相邻的几个未知数的积的系数记入相应的夹缝中. 我们用 x、y、z、u 分别表示天、地、人、物四元,那么它们在四元式中的位置如下图 3 所示:【图略】
图 4 表示方程 - x2+ 3xy - 2xz + x - y = 0四元消法是朱世杰方程理论的核心. 他通过方程组中不同方程的配合,采用“剔而消之”、“易位”、“互隐通分”、“内外行乘积”等方法.【公式4】
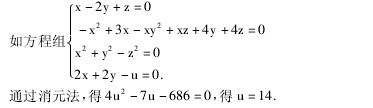
吴文俊先生指出:“天元术起于宋代而发展到元代,已经发现了解高次联立方程组的途径与处理方法.‘八五’期间攀登项目中解多项式方程组的一个主要方法———特征列法,即源自元朱世杰《四元玉鉴》的四元术……”. 吴文俊先生称所创立的“吴消元法”借鉴了中国古代解方程组的思想,尤其是朱世杰四元术中可机械执行的消元法思想.对前人方程问题的研究与探讨,不仅可以追溯数学内容、思想和方法演变、发展过程,而且还从古人的成果中汲取养分,做到古为今用,推陈出新. 我国着名数学家吴文俊先生在拓扑学研究方面取得过杰出成就,其后,他在研究整理古代数学方程理论与方法方面开创了新局面,建立了被誉为“吴方法”的数学机械化方法,成为古为今用的典范,其意义是重大的.
参考文献:
[1] 孙宏安. 朱世杰与“四元术”[J]. 数学通报,1997,(3):45-46.
[2] 胡明杰. 四元术的数学基础[J]. 北京师范大学学报(自然科学版),1991,(4):494-495.
[3] 刘洪元. 吴消元法与四元术[J]. 辽宁大学学报(自然科学版),2004,(4):130-131.





