
1关系
宇宙万物之间存在着形形色色的联系,这种联系正是各门学科所关注的根本问题。 例如,人与人之间有父子、兄弟、师生关系;两数之间有大于、等于、小于关系;电学中有电压、电阻与电流间的关系;元素与集合之间的属于关系;计算机科学中程序间的调用关系,程序执行过程中状态之间的转换关系,程序执行前变量取值状况和执行后变量取值状况的关系,文件与路径的关系……集合论为刻划这种联系提供了一种数学模型---关系,它仍然是一个集合,以具有那种联系的对象组合为其成员。换言之,集合论中关系不是通过描述关系的内涵来刻划这种联系,而是通过列举其外延(具有那种联系的对象组合全体)来刻划这种联系。这使关系的研究可以方便地使用集合论概念、运算及研究方法和研究成果。
1.1 关系的定义
在关系模型中,数据是以二维表的形式存在的,这个二维表就叫做关系。关系理论是以集合代数理论为基础的,因此,我们可以用集合代数给出二维表的关系的定义。 为了以集合论的角度给出关系的定义,我们先引入笛卡尔积的概念。在定义笛卡尔积之前,先来了解有序对的定义。
定义 1 由两个元素 x 和 y(允许 x=y)按一定的顺序排列成的二元组叫做一个有序对(也称序偶),记作<x,y>.其中 x 是它的第一元素,y是它的第二元素。
一般说来有序对具有以下特点:(1)当 x≠y 时,<x,y>≠<y,x>;(2)两个有序对相等,即<x,y>=<u,v>的充分必要条件是 x=u 且 y=v.这些特点是集合{x,y}所不具备的,例如,当 x≠y 时,有{x,y}={y,x}.原因在于有序对<x,y>中强调了 x 与 y 的序列性,而集合{x,y}中的 x 和y 是无序的。定义 2 一个有序 n 元组(n≥3)是一个有序对,其中第一个元素是一个有序 n-1 元组,一个有序 n 元组记作<x1,x2,…,xn>,即<x1,x2,…,xn>=《x1,…,xn-1>,xn>.
下面定义给出笛卡尔积的定义,它是一种集合运算。定义 3 设 A、B 为集合, 用 A 中元素为第一元素,B 中元素为第二元素,构成有序对。所有这样的有序对组成的集合叫做 A 和 B 的笛卡尔积,记作 A×B.符号化表示为A×B={<x,y>|x∈A∧y∈B}.例 1 A={a,b},B={0,1,2},则A×B={<a,0>,<a,1>,<a,2>,<a,2>,<b,0>,<b,1>,<b,2>};B×A={<0,a>,<0,b>,<1,a>,<1,b>,<2,a>,<2,b>}.由排列组合的知识不难证明,如果 A 中有 m 个元素,B 中有 n 个元素,则 A×B 和 B×A 中都有 mn 个元素。
下面研究与笛卡尔积密切相关的一个重要概念---二元关系。
在现阶段我们用的最多的是二元关系,所谓二元关系就是在集合中两个元素之间的某种相关性。例如,甲、乙、丙 3 个人进行乒乓球比赛,如果任何两个人之间都要赛一场,那么共要赛三场。假如三场比赛的结果是乙胜甲、甲胜丙、乙胜丙,这个结果可以记作{<乙,甲>,<甲,丙>,<乙,丙>},其中<x,y>表示 x 胜 y.它表示了集合{甲,乙,丙}中元素之间的一种胜负关系。
除了二元关系以外,还有多元关系,在此不做讨论。下面出现关系的地方均指二元关系。下面给出二元关系的一般定义。
定义 4 如果一个集合为空集或者它的元素都是有序对,则称这个集合是一个二元关系,一般记作 R.对于二元关系 R,如果<x,y>∈R,则记作 xRy;如果<x,y>埸R,则记作 .
定义 5 设 A、B 为集合,A×B 的任何子集所定义的二元关系称作从 A 到 B 的二元关系,特别当 A=B 时,则叫做 A 上的二元关系。对于任何集合 A 都有 3 种特殊的关系。 其中之一就是空集 ,它是 A×A 的子集,也是 A 上的关系,称作空关系。另外两种就是全域关系 EA和恒等关系 IA.
定义 6 对任何集合 A,EA={〈x,y〉|x∈A∧y∈A}=A×A IA={〈x,x〉|x∈A}
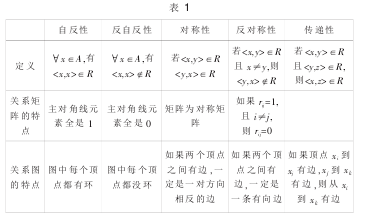
1.2 关系的性质在一个很小的集合上就可以定义很多个不同的关系,但是真正有实际意义的只是其中很少的一部分,它们一般都是有着某些性质的关系。设 R 是 A 上的关系,R 的性质主要有以下 5 种:自反性、反自反性、对称性、反对称性和传递性。它们的定义及其在关系矩阵中的特征如表 1 所示。
根据表 1 所列的特点不难判断关系的性质。例如,集合 A 上的全域关系和恒等关系是自反的、对称的和传递的。整除关系、小于等于关系和幂集上的包含关系是自反的、反对称的和传递的。
2在密码学中的应用
在离散数学中有一种关系---同余关系,面我们来看看它的具体定义。
定义 4 给定正整数 m,若用 m 去除两个整数 a 和 b 所得余数相同,称 a 和 b 对模 m 同余,记作 a≡b(mod m),并称该式为同余式。对于给定的 b 和 m,与 b 模 m 同余的所有数为:b+km,其中 k=0,±1,±2,±…同余关系具有以下性质:
(1)自反性 a≡a(mod m)。
(2)对称性 若 a≡b(mod m),则 b≡a(mod m)。
(3)传递性 若 a≡b(mod m),b≡c(mod m),则 a≡c(mod m)。
不难看出,同余关系是一种等价关系。实际应用中,我们将这种关系推广到了密码学中,先看一下下面这个例子。
例 凯撒密码这是一个古老的加密方法,当年凯撒大帝行军打仗时用这种方法进行通信,因此得名。它的原理很简单,其实就是单字母的替换。看一个简单的例子:“This is Caesar Code”. 用凯撒密码加密后字符串变为“vjku ku Ecguct Eqfg”.看起来似乎加密得很“安全”.可是你 可以尝试一下,把这段很难懂的东西每一个字母换为字母表中前移 2 位的字母……哦,结果出来了。
凯撒密码的字母对应关系:A b c d e f g h i … x y zC d e f g h I j k … z a b ([1]) ,从这个例子不难看出, 实际上就是模为 2 的同余关系的一种应用。再来看下面一个例子。例 (rot13)ROT13 是网络上常见的一种简单的“加密”方式。它的原理和凯撒密码非常类似。 凯撒密码移了 2 位, 而ROT13 移了 13 位。ROT13 通常作为简单的手段使得我们的电子信件不能被直接识别和阅读,也不会被那些匹配程序用通常的方法直接找到。
如“V Ybir lbh! ”这个句子实际上是“I Love you! ”.ROT13 字母对应关系:A b c d e f g h I … x y zN o p q r s t u v … k l m ([2])
参考文献:
[1][美]Paul Garrett.密码学导引[M].北京:机械工业出版社,2003:107-178.
[2]斯汉.密码学与计算机网络安全[M].北京:清华大学出版社,2001:17-58.
[3]耿素云,屈婉玲,张立昂,编。离散数学。3 版。北京:清华大学出版社,2004,3.





