摘 要: 迷宫寻路问题是人工智能领域实际应用的一个重要体现,如何表示状态空间和搜索路径是寻路问题的研究重点,本文从离散数学的角度研究迷宫寻路问题,分别用谓词逻辑和广度优先搜索解决迷宫寻路问题。本文通过具体的迷宫路径图进行分析,谓词逻辑通过定义状态谓词、操作符,列举所有可能的路径解决迷宫问题;广度优先搜索将迷宫看作图的遍历,逐层扫描直到扫描到终点,并保存扫描路径最终找到迷宫求解路径。
关键词: 迷宫寻路; 谓词逻辑; 广度优先搜索;
迷宫寻路问题本质上属于人工智能中路径搜索分支,解决迷宫寻路问题对于人工智能中游戏设计具有重要的指导意义[1]。谓词逻辑接近于人类的自然语言,在早期人工智能表示方法中广泛应用在计算机存储表示中。广度优先搜索通过队列存储迷宫路径节点,因此若给定起点和终点且存在最优路径,通过广度优先搜索求解出的路径一定属于最优路径,对于解决迷宫问题有着显着优势。

1、 谓词逻辑与迷宫寻路问题
1.1、 问题提出
迷宫的每一个格子,对应一个状态。设有迷宫的大小为6×7,共有42个状态,如图1所示。初始状态为41,目标状态为2和5。对于迷宫中的每个状态,在它的上下左右四个方向中,如果某个方向没有墙,则可以走进下一个状态[2]。
图1 迷宫图
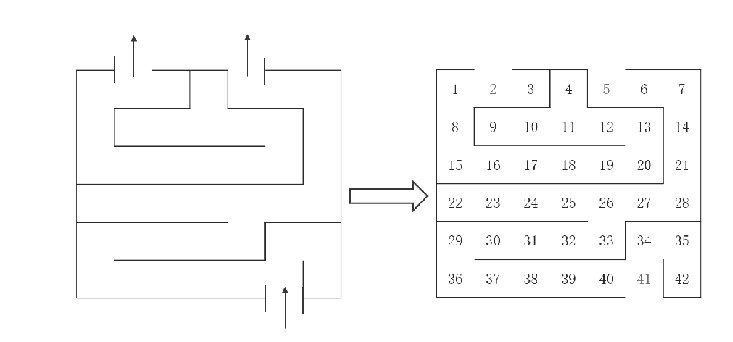
图2 迷宫矩阵表示
1.2、 问题分析
根据定义所需求解问题,首先定义表示事物状态的谓词,AT(person,x)表示person位于位置x处,Start(x)表示位置x是起始位置,End(x)表示位置x是终点位置,Pass(x,y)表示位置x和位置y合法,且相邻,且无阻隔;定义表示事物状态的谓词,设初始状态AT(person,41),最终求解得到目标状态AT(person,2)或AT(person,5);定义操作符Move(person,x)表示从位置x向上下左右移动;假定条件AT(person,x)表示当前在节点x处;定义动作谓词Goto(x,y)表示从x走到y;定义条件:AT(person,x)∧Pass(x,y)表示删除AT(person,x),添加AT(person,y)。
1.3 、问题求解
通过推理可以获得一条路径:AT(person,41)→AT(person,40)→AT(person,39)→AT(person,38)→(person,37)→AT(person,36)→AT(person,29)→AT(person,30)→AT(person,31)→AT(person,32)→AT(person,33)→AT(person,26)→AT(person,27)→AT(person28)→AT(person,21)→AT(person,14)→AT(person,7)→AT(person,6)→AT(person,5)(而无法达到位置2)。
2 、广度优先搜索与迷宫寻路问题
2.1、 问题提出
广度优先搜索采用的数据结构是队列,利用队列先进先出的特点,来模拟走迷宫的过程。
2.2 、问题分析
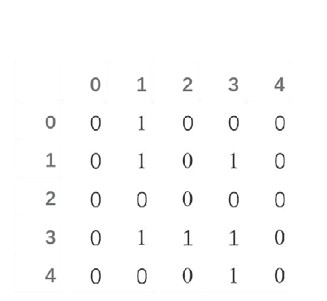
以不含多条出路,不带环的简单迷宫为例,以1为障碍物、0为可行路,且仅可上、下、左、右行走;且假设均可到达终点,模拟计算机中走迷宫的过程,用矩阵存储迷宫图,如上图2。
2.3 、问题求解
定义初始化条件,设输入起点(0,0),终点(4,4),定义空队列Q={},表示当前无可行点;得到输出路径队列Qp;算法执行过程如下:首先起点加入队列Q={(0,0)};其次取出队列Q中头结点Vn,Vn=(0,0),Vn加入队列Qp={(0,0)};Q={};然后取出Vn所有相邻节点,判断:相邻节点需满足未被访问且节点值不为0;不含终点(4,4),加入队列Q,Q={(1,0)};重复以上步骤直至到达终点。
3、 结语
对于迷宫问题求解,除了上文中不含多条出路,不带环的简单迷宫,还有不带环的多通路迷宫、带环迷宫,均可采用广度优先搜索找到通路[3]。利用谓词逻辑寻找迷宫求解策略,需要定义状态谓词及操作符,谓词逻辑解决迷宫问题可读性强,但是对于复杂迷宫问题的求解会出现组合爆炸[4,5]等问题。利用广度优先搜素寻找最短路径先访问到的目标一定是,层数最少的即路径最短的,但也存在一定的局限性,广度优先搜索假定了路和路之间的代价是相同的。
参考文献
[1]杨科选.人工智能寻路算法及其在游戏中的应用研究[D].长沙:中南大学,2009.
[2]徐瑛蔚.基于分布式存储的大规模图的深度优先搜索算法研究[D].沈阳:辽宁大学,2018.
[3]罗敏娜,侍啸.贪心优化的搜索算法在RGV动态调度中的应用[J].沈阳师范大学学报(自然科学版),2019,37(04):315-320.
[4]杨红棉.浅析逻辑语义学的基本观点——命题逻辑与谓词逻辑[J].农家参谋,2019(22):269.
[5]薛晓亚.利用栈与队列实现迷宫游戏[J].信息与电脑(理论版),2018(11):94-95.





