摘要：离散数学是计算机专业的专业基础课, 它的四个部分数理逻辑、集合论、代数结构、图论分别是相对独立的分支, 但都是对离散对象的讨论, 因此它们之间仍然有着或深或浅的联系。文章探讨各部分在教学中的相关性, 找出它们共性的部分, 使其在教学中相互关联、相互融合, 以加深学生掌握知识的熟练度, 提高学习效率。
关键词：离散数学; 相关性; 教学;
Discussion on the Correlation of the Contents of Discrete Mathematics
Abstract：
Discrete Mathematics is a specialized basic course of computer science. Its four parts, mathematical logic, set theory, algebraic structure and graph theory, are relatively independent branches, but they all discuss discrete objects, so there are deep or shallow connections between them. In order to improve the proficiency of students in discrete mathematics knowledge, this paper discusses the correlation of the four parts in the teaching to find out their common part and make them to interrelate and integrate each other in the teaching.
Keyword：
discrete mathematics; correlation; teaching;
离散数学课程是计算机专业的核心基础课, 主要研究离散量的结构和相互关系。学习该课程可以培养学生的逻辑推理能力、抽象思维能力、缜密概括能力, 并且为后续的专业课如数据结构、数字逻辑电路、数据库等作基础[1]。
离散数学主要包括四个部分的内容:数理逻辑、集合论、代数结构、图论。数理逻辑主要研究离散对象的推理和形式化方法, 集合论研究离散结构的表示和描述工具, 代数结构研究离散结构的代数模型, 图论研究离散结构的关系模型。长期以来, 这四个部分呈现的特点就是“内容散”, 各部分之间的联系不紧密[2]。这种情况会导致学生学到后面部分的内容时, 对前面已学习的内容容易遗忘。
事实上, 四个部分都是对离散对象进行讨论, 它们之间仍然有着或深或浅的联系。在教学实践中, 为了避免学生遗忘前期所学知识点, 使学生在学习新知识的同时也能关联复习前面的内容, 现对各部分知识的相关性进行探讨并总结归纳如下。
1 集合论与数理逻辑
(1) 数理逻辑描述离散对象的形式化方法, 提供了集合部分的表示方法。集合的表示方法有列元素法和谓词表示法, 列元素法是把集合的元素都列举出来, 而谓词表示法采用的就是数理逻辑的描述方法, 描述集合的元素满足的条件, 如集合A={3, 4, 5}是列元素表示法, 用谓词表示法表示为A={x|x∈Z∧2<x<6}。
集合运算的定义形式也采用谓词表示法, 如集合的广义交运算, ∩A={x|?z (z∈A→x∈z) }[3], 定义中元素x满足的条件用谓词描述, 元素x满足的条件为对A所有的元素z, x都是z的元素, 即集合A的所有元素的公共元素构成的集合。
(2) 集合运算的主要算律与命题逻辑的等值式算律相近, 如都具有幂等律、交换律、结合律、分配律、双重否定律、德摩根律、吸收律、排中律、矛盾律等, 如集合运算的吸收律A∪ (A∩B) =A, 逻辑运算的吸收律A∨ (A∧B) ?A, 又如逻辑运算的德摩根律? (A∨B) ??A∧?B, 在集合运算中绝对补运算也有德摩根律? (A∪B) =?A∩?B, 相对补运算也有德摩根律, 比如对C的相对补运算满足C- (A∪B) = (C-A) ∩ (C-B) 。将这些运算性质对比学习, 一方面可以复习巩固已学知识, 另一方面也有助于对新知识的理解。
(3) 集合论部分的常用证明方法之一命题演算证明法, 是根据运算的定义用数理逻辑的等值式或者推理进行证明。如果证明X?Y:任取x, x∈X?…?x∈Y;如果证明X=Y:任取x, x∈X?…?x∈Y。
例如用命题演算法证明关系的复合运算对并运算的分配律, F° (G∪H) =F°G∪F°H,
任取<x, y>,
<x, y>∈F° (G∪H)
??t (<x, t>∈F∧<t, y>∈G∪H) ……复合运算的定义
??t (<x, t>∈F∧ (<t, y>∈G∨<t, y>∈H) ) ……并运算的定义
??t ( (<x, t>∈F∧<t, y>∈H) ∨ (<x, t>∈F∧<t, y>∈H) ) ……逻辑运算∧对∨的分配律
??t (<x, t>∈F∧<t, y>∈G) ∧?t (<x, t>∈F∧<t, y>∈H) ……一阶逻辑量词分配等值式
?<x, y>∈F°G∧<x, y>∈F°H……复合运算的定义
?<x, y>∈F°G∪F°H……并运算的定义
所以有F° (G∪H) =F°G∪F°H。
命题演算的证明法充分利用了数理逻辑的研究内容, 即对离散对象的推理和形式化方法。将集合论与数理逻辑结合起来学习, 有助于学生更好地理解和掌握两部分内容。
2 代数结构与集合论
(1) 代数系统的二元运算和一元运算是以函数的形式定义的, 如设S为集合, 函数f∶S×S→S称为S上的二元运算, 对于运算f (<x, y>) =z, 也可以用运算符表示为x○y=z, 对于一元运算, 称函数f∶S→S为S上的一元运算, 对于运算f (x) =y, 也可以用运算符表示为*x=y。
(2) 在讨论二元运算的运算性质和特异元素的时候, 也常常以集合中的运算为例作分析。
例如讨论幂集P (S) 上的∪、∩、⊕运算, ∪和∩满足幂等律、交换律、结合律、分配律、吸收律等, ∪运算的单位元是?, 零元是S, ∩运算的单位元是S, 零元是?。⊕运算满足交换律、结合律、消去律, 不满足幂等律, 单位元是?, 每个元素A的逆元是A。又如对于AA中函数的复合运算, 满足结合律, 不满足交换律、幂等律、消去律, 单位元是IA, 双射函数有逆元, 是其反函数f-1。
以这些集合论中的运算为例来讨论, 可以在学习运算性质和特异元素的定义的同时, 对前面所学知识再次进行复习, 同时加深对两部分内容的理解。
(3) 讨论代数系统中的陪集时, 将陪集与二元关系的等价类进行关联讨论, 可以更深入地探讨陪集的性质。
设G是群, H是G的子群, 在G上定义二元关系R:?a, b∈G, <a, b>∈R?ab-1∈H, 则R是G上的等价关系, 且[a]R=Ha[3]。根据定义可知, a关于R的等价类就是以a为代表元素的H的右陪集, 因此陪集就有了等价类的特点和性质。在这一部分, 可以同时复习等价关系的定义, 对R是等价关系进行分析, R满足自反性?a∈G?<a, a>∈R;R满足对称性, ?<a, b>∈R?<b, a>∈R;R满足传递性, ?<a, b>∈R∧<b, c>∈R?<a, c>∈R。另外复习等价类的性质并转换为陪集的性质, 如每个陪集 (等价类) 都是集合G的非空子集, 任意两个陪集 (等价类) 或者相等或者不交, 所有陪集 (等价类) 的并即为G, 并可以根据这些性质引入拉格朗日定理。
(4) 代数系统中的格的定义是集合论中的偏序集, 设<S, ?>是偏序集, 如果?x, y∈S, {x, y}都有最小上界和最大下界, 则称S关于偏序?作成一个格。
3 图论与集合论
(1) 图是以集合的形式定义的, 包括顶点集V和边集E, G=<V, E>。
(2) 有向图与二元关系相关, 都有三种表示法:集合、矩阵、图形。
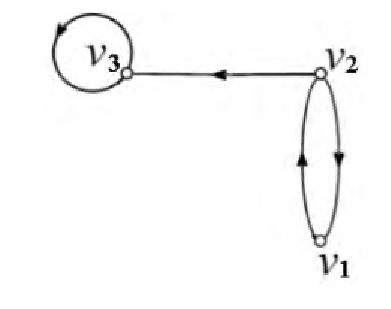
设有向图D=<V, E>, V={v1, v2, v3}, E={<v1, v2>, <v2, v1>, <v2, v3>, <v3, v3>}, 其图形表示如图1所示, 根据点与点之间的邻接关系得到邻接矩阵
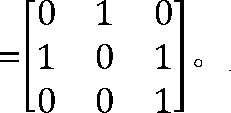另外也可以从二元关系的角度来看, 设集合S={v1, v2, v3}, 集合S上的二元关系R={<v1, v2>, <v2, v1>, <v2, v3>, <v3, v3>}, 则图1即为二元关系R的关系图GR, A (D) 就是关系R的关系矩阵MR。
图1 有向图D
此外, 可达关系反映的是有向图中两点间是否存在通路的情况, 可以用可达矩阵P (D) 来表示, 当假定图中每个点到自身是可达的, 可达关系具有传递性。可达矩阵P (D) 反映在二元关系中就是关系R的传递闭包t (R) 。
(3) 无向图的连通性与等价关系的概念相关联。在无向图中讨论顶点之间的连通关系, 设G=<V, E>为无向图若u、v∈V之间存在通路, 则称u?v。规定, ?v∈V, v?v。由连通的定义可知, ?是V上的等价关系, R={<u, v>|u, v∈V且u?v}, 满足自反性, ?v∈V?v?v?<v, v>∈R, 满足对称性, ?<u, v>∈R?u?v?v~u?<v, u>∈R, 满足传递性, ?<u, v>∈R∧<v, w>∈R?u?v∧v~w?u~w?<u, w>∈R。根据等价关系, 顶点集V中的每个点都有等价类, [v]={u|v~u且u∈V}。假设Vi是V关于顶点之间的连通关系~的一个等价类, 称其导出子图G[Vi]为G的一个连通分支。G的连通分支数记作P (G) 。
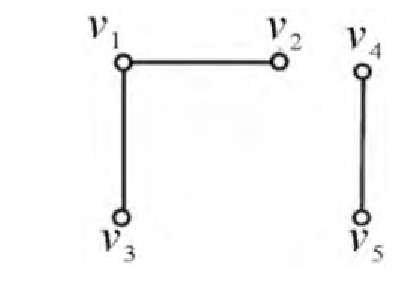
例如, 无向图G如图2所示, 顶点集关于连通关系分为两个等价类, [v1]=[v2]=[v3]={v1, v2, v3}, [v4]=[v5]={v4, v5}, 等价类{v1, v2, v3}的导出子图为一个连通分支如图2左边, 等价类{v4, v5}的导出子图为另一个连通分支如图2右边, 连通分支数P (G) =2, 即为不同等价类的个数。
图2 无向图G
(4) 在二元关系部分, 求二元关系R的传递闭包t (R) 有三种方法:集合表达式、关系矩阵、关系图。在通过R的关系图GR求传递闭包t (R) 的关系图Gt时, 考察G的每个顶点xi, 找从xi出发的所有1步、2步、3步、…、n步长的路径 (n为GR的顶点数) 。如果有从xi到xj的步长为1或2或…或n的路径, 就在Gt中加上一条从xi到xj的边, 在检查完所有的顶点后就得到传递闭包的关系图Gt。在此过程中, “为什么找到步长为n以内的路径, 而再长的路径不需要找了”, 这一点可以在图论中找到依据。
图论中关于通路的性质, 在n阶图G中, 若从顶点vi到vj (vi和vj可能相同也可能不同) 存在通路, 则从vi到vj存在长度小于或等于n的路径。也就是说, 如果从vi到vj没有长度小于或等于n的路径, 那么从vi到vj就没有任何长度的通路。所以判断从vi到vj有没有通路, 只需要找长度为n以内的路径就可以了。
4 图论与代数结构
图论与代数结构中都有同构的概念, 都指的是保持结构的双射函数。
在代数结构中, 设V1=<A, ○>和V2=<B, *>是同类型的代数系统, f:A→B是双射函数, 且对于?x, y∈A有f (x○y) =f (x) *f (y) , 则称f是V1到V2的同构映射, 记作V1?V2。
在图论中, 可以类比讨论上面的同构的概念。设G1=<A, E1>和G2=<B, E2>是两个图, 有向图中的边可以表示为点的有序对, 如<v1, v2>=e1, 这种对应关系可以用函数来表示, 用函数g1:A×A→E1和g2:B×B→E2分别表示图G1和图G2中的有向边, 它们分别对应二元运算○和*, 则关于双射函数f:A→B, 对于?x, y∈A, <x, y>∈E1当且仅当<f (x) , f (y) >∈E2, 则称G1与G2是同构的, 记G1?G2。
5 函数与二元关系
函数与二元关系都是集合论中的内容, 函数是一种特殊的二元关系。在学习过程中, 先学习二元关系, 再学习函数。在函数中有几个常用函数, 与二元关系相关, 可以在学习函数的过程中, 对二元关系的内容进一步复习巩固。
(1) 单调函数。设<A, ?>, <B, ?>为偏序集, f:A→B, 如果对任意的x1, x2∈A, x1?x2, 就有f (x1) ?f (x2) , 则称f为单调递增的;如果对任意的x1, x2∈A, x1?x2, 就有f (x1) ?f (x2) , 则称f为严格单调递增的[3]。
例如, 偏序集<P ({a, b}) , R?>, <{1, 2, 3}, ≤>, R?为包含关系, ≤为一般的小于等于关系, 令f:P ({a, b}) →{1, 2, 3}, f (?) =f ({a}) =1, f ({b}) =2, f ({a, b}) =3, 则f满足单调递增, 比如对??{b}, 有f (?) =1≤f ({b}) =2, 但该函数不满足严格单调递增。
(2) 自然映射。设R是集合A上的等价关系, 令g:A→A/R, ?a∈A, g (a) =[a], 称g是从A到商集A/R的自然映射[3]。
例如, A={a, b, c}, R是A上的等价关系, R={<a, c>, <c, a>}∪IA, A/R={{a, c}, {b}}, g:A→A/R, g (a) =g (c) ={a, c}, g (b) ={b}, 函数g称为自然映射, 是满射函数。
6 结束语
离散数学各部分虽然较为独立, 但是它们之间仍然有着一定的相关性, 在学习过程中可以强调这几个方面的联系, 使学习的内容前后关联、相互融合, 知新并温故, 能够帮助学生更深刻地理解并掌握离散数学的知识。
参考文献
[1]王敏, 韩俊英.关于离散数学各部分内容之间关系的初探[J].甘肃科技, 2010, 26 (11) :60-61.
[2]谢志强.讲好离散数学的第一次课[J].计算机教育, 2011 (16) :95-98.
[3]屈婉玲, 耿素云, 张立昂.离散数学[M].北京:高等教育出版社, 2008.
