
数学模型是描述一个系统或性质的数学形式,具体形式有图形、数据表、方程、不等式、函数等.《普通高中生物课程标准》将“模型”知识列为课程目标之一,提出领悟系统分析、数学模型等科学方法及其在科学研究中的应用要求.
一、高中生物教学中构建数学模型的方法和步骤
在新课标生物必修3的第4章《种群和群落》中的第2节《种群数量的变化》中,教材以“微生物种群数量的变化”为例,构建数学模型.
(一)模型准备要构建一个数学模型,首先我们要了解问题的实际背景,明确建模的目的,并搜集必需的各种资料和信息,尽量弄清楚对象的特征.在这一数学模型的构建中,研究对象是“细菌”,其特征是“进行二分裂,每20min分裂一次”,建模的目的是探究细菌种群数量的变动特点,进一步解释生物现象,揭示生命活动规律.
(二)模型假设根据对象的特征和建模目的,对问题进行必要的、合理的简化,用精确的语言作出假设,是建模至关重要的一步.假设不同,所建立的数学模型也不同.如此建模中提到的假设是“在资源和空间无限多的环境中,细菌种群的增长不会受到种群密度增加的影响”,也就是在“理想的环境中,此环境一般指的是资源和空间充足,气候适宜,没有天敌,没有疾病等”.
(三)模型建构根据所作的假设分析对象的因果关系,利用对象的内在规律和适当的数学工具,构造各个量词的等式关系或其他数学结构.这时,我们便会进入一个广阔的应用数学天地.不过我们应当牢牢记住,构建数学模型是为了让更多的人明了并能加以应用,因此工具越简单越有价值.
通过上述的分析,得出细菌增殖的特点是以满足指数函数的形式进行增长,因此用数学形式表达为Nn=2n,其中N代表细菌数量,n代表第几代.
(四)模型求解一道实际问题的解决往往需要纷繁的计算,可以采用解方程、画图形、证明定理、逻辑运算、数值运算等各种传统的和近代的数学方法进行模型的求解.
如在这一数学模型的构建中,我们根据刚才的指数函数模型把细菌的数量进行计算统计,把数据进行整理,此时构建出另一种数学模型---表格(如表1)。【1】
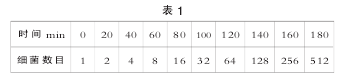
表格具有一定的局限性,因此我们还可以把它构建成坐标图的数学模型.利用建立坐标图像使一些抽象的知识变得更具体,从而得到了在理想的环境中生物种群的一种增长曲线---“J型增长曲线”.
(五)模型修正完善生物学的大量现象与规律是极为复杂的,存在着许多不确定因素和例外的现象,在对模型解答进行数学分析基础上,并通过实验或观察对原先的模型进行补充或扩充、检验和修正,使学生认识到模型的构建是一个不断发展和完善的过程.
如让学生进一步思考问题:
(1)其他的生物并不一定进行二分裂的生殖方式,那么它们的种群数量的变化是否也满足上述的“J型增长曲线”呢?如果满足那么它的函数模型又是怎样呢?通过进一步的假设分析,得到Nt=Noλt,其中No为该种群的起始数量,t为时间,Nt为t年后该种群的数量,λ为该种群每年增长倍数.
(2)生物的实际生活环境是否真的这么理想呢?
让学生对在实际环境(如资源和空间有限,气候并不一直适宜,出现天敌和竞争者,同时还会受到疾病等的威胁中生物种群的数量变化进行进一步的假设分析,得出在自然界中,种群不能无限增长,因为它不仅受到物理因素和生物因素的制约,而且随着种群数量的不断增长,制约因素的作用也在增大,使出生率和死亡率达到一定的平衡,种群总是在增长到一定限度后达到相对的稳定,因此构建出另一增长曲线---“S型增长曲线”.
二、高中生物教学中构建数学模型经典例析
数学模型的建立:确定自变量、因变量或其他参数;建立变量间的数量关系,以图形、数据表、方程、不等式、函数等形式表现出来;检验和修正(见表2)。人教版必修2教材P14之“四、思维拓展”:
根据两对相对性状的遗传分析,讨论3-n对相对性状的遗传结果,用数学式表示(见表3)。【2】

进行数据模型建立训练的知识点举例:遗传平衡中的基因频率计算;生态系统第n营养级的能量值范围;DNA以及肽链种类的多样性计算.
在生物学科中进行构建数学模型思维的渗透,把复杂的研究对象转变为数学问题,经过合理简化后,建立一个能用数学方法揭示研究对象规律的数学关系式,不仅可以使学生体会到生物学并非是一门理解型的自然科学,而且可以使学生感觉到利用构建数学模型的思维结合生物学理论知识,很好地解决一些生物学实际问题,能使学生的知识能发生正迁移,起到举一反三的效果.而且数学模型在生物实验中还有着重要的意义,能进行数量大的分析处理,从而克服了实际实验中只能对少数生物进行分析的局限:能够将复杂的多因素以独立的形式进行分析,能重复研究实验的各种信息、资料,这些都是在实际实验中很难做到的.
由此看来,通过构建数学模型,以繁化简,让学生获得知识,同时也获得知识习得的方法.





