
我朋友下岗后经营卖鸡业务, 鸡厂规定:(1)在每个季度内,订户每月每天从鸡厂里采购的鸡的数量必须相同,零售不完不予回收;(2) 购 1—49 只鸡执行市场零售价 50元/只,50-100 只鸡享受批发价 48 元/只,100只以上享受批发价 45 元/只。 由于 饲 养 不便,卖鸡者不能留鸡过夜,而市场中有一饭馆,每天收购鸡的价格是 42 元;我朋友把他三月份卖鸡的情况作了记录,并要求我依据记录,利用数学统筹帮他决定下季度,每月每天与鸡厂签订的合同订购鸡的数量,以便他每月能获得最大利润。
三月份每天进鸡 95 只, 支出 4560 元,依据朋友的记录情况, 我制作统计表如下(表 一)。
由表 1 知。 若每天所需鸡的数量越多,该盈而损失价格每只(50-48)元的倍数就越大,(鸡只数×天数)×(50-48) 的值越大,因此, 进量不足导致的损额累计 m1的和就越大; 若每天多进鸡的数量越多,则卖不掉被饭馆回收而跌损价格每只(42-48)元的倍数就越大,(鸡只数×天数)×(42-48) 的绝对值越大,因此,采购数量超多导致的损额累计m2负的和的绝对值越大。
易知,若 m1>m2的绝对值,则订购时需要增加订购数量.
若 m1<m2的绝对值,则订购时需要减少订购数量.
若 m1=m2的绝对值,则订购时订购数量不增不减。
这里 ,m1=(50 -48) ×(1 ×0 +2 ×1 +3 ×0 +4 ×1 +5 ×0 +6 ×2 +7 ×5 +8 ×5 +9 ×5 +10 ×6) =2 ×198 =396;m2=(42-48)×(1×2+2×0+3×1+4×0+5×0+6×0)=-6×5=-30;m 损=396+(-30)=366.
显然,m1=396>|m2|—=30;说明每天所需鸡的数量总体大于当天采购鸡的数量,订购下季度每月每天鸡的数量时, 需增加订购数量,设每月每天需增加 x 只,那么,每天增加收入 (50-48)x=2x 元, 若每月按照 30 天计算, 则每月增加收入 30×2x 元, 由于 m 损=m1+m2=520-30=490,从 而 ,30×2x=490, 解得x=8.16≈8.
于是,下季度每月每天订购鸡 95+8=103(只)时 ,盈利最多 。
检验:若每天按照 103 只计算,则表一变为表二。
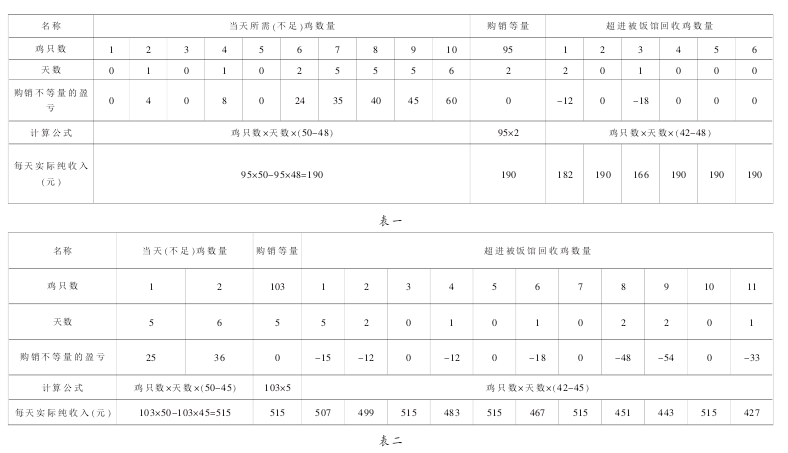
所需鸡的数量不足导致的损额 m1 损=(50-45)×(1×5+2×6)=5×17=85.
超进鸡的数量被饭馆低价收购损额 m2损=(42-45)×(1×5+2×2+3×0+4×1+5×0+6×1+7×0+8×2+9×2+10×0+11×1)=-3×75=-225.
显然,m新 损=m1 损+m2 损=85+(-225)=-140<m损=366.
因此,每天订购 103 只鸡,效益会更好。
按照三月份的销售情况看, 若每月订购鸡的数量 103 只,按照每月 30 天计算,则实际 收 入 可 达到 103×(50-45)×30+(42-45)×(1×5+2×2+3×0+4×1+5×0+6×1+7×0+8×2+9×2+10×0+11×1)=15450+(-225)=15225(元 ),而原来收入 95×(50-48)×30+(42-48)×(1×2+2×0+3×1+4×0+5×0+6×0)=5700-30=5670(元).
由此可知,按照数学统筹方法进行订购卖鸡,每月多盈利 15225-5670=9555(元)。
本文通过数学统筹在卖鸡中的应用,总结一下几点。
1.启迪人们对数学的爱好,增强探索数学,应用数学的激情;
2.说明市场营销和再就业应用数学统筹的科学方法,效益会更好;
3.本文把数学知识运用于对自主创业的指导, 这是素质教育推行的创新能力的导向,具有很高的价值。





